1. 提要
从这个系列文章的第四篇开始,我们开启了机器学习可行性的讨论。在第四篇中,我们经过了“天下没有白吃的午餐 (No Free Lunch)”的考验,了解了“No Free Lunch”定理的前提假设,也得知了在具体的现实问题中,使用与问题匹配的学习算法可以取得很好的效果。
现在我们将继续出发,带上最初开启这个主题时的终极疑惑 ——
你敢跟着机器学习投资吗?
那个由训练数据也就是历史日志学得的模型,真的能在未来的预测中表现的一样好吗?
如果说上一篇还是在努力拨开 No Free Lunch 的迷雾,这一篇我们将真正展开学习可行性的定量分析和讨论。
它属于机器学习的研究方向之一——计算学习理论 (Computational Learning Theory)。
可能有的人觉得它过于枯燥,有的人觉得它太过理论。不过我要说,计算学习理论回答的是机器学习“为什么可以学习”的终极疑问,它不仅是机器学习的理论基础,更是一切高楼的基石。不理解这部分机器学习的理论基础,一切的学习算法和模型都将沦为脚下悬空的招式。不得心法,将永远是被拦在半掩大门外的”门外汉“。
不过在正式进入主题之前,首先要对再次的跳票感到抱歉。我完全错误地估计了这个主题的内容量和写作难度。从最初妄想一篇搞定,到上周改成上、下两篇,再到刚刚看了一眼,第五篇的字数已超5000+资料查阅和写作时间超过20小时,却仍然只完成了原计划下篇内容的一半。非常抱歉,这个主题的写作时间将再次延长,分成上、中、下三篇。
当然,跳票的反面也意味着这个系列文章的初心的坚持 —— 追求把复杂的东西变简单,追求简洁明了,追求直接易懂。
站在巨人们的肩膀之上,我努力让这个主题的写作冲击史上最好的计算学习理论的讲解。是的,我把“之一”都去掉了。
整个讲解仅有 3 步,讨论完 3 种情况之后我们就可以回答这个终极的疑问:
股市中我们根据历史数据学到了一个准确率为的模型,这个模型在未来的预测表现能向
看齐吗?未来的准确率
与
之间有着怎样的关系?
2. 第一种情况——Hypothesis Set 中只有一个 hypothesis 的情况
第一种情况,我们首先看看 Hypothesis Set 中只有一个 hypothesis 时会发生什么。
当 Hypothesis Set 中只有一个 hypothesis 时,模型的预测准确率与训练准确率的关系可以类比成一个相当好理解的例子——人口调查。
图1:
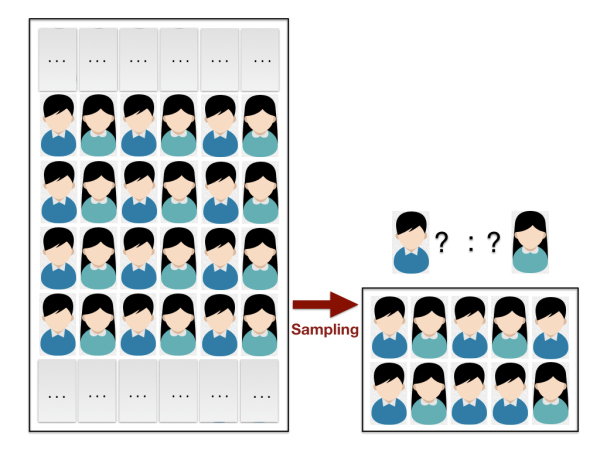
如图 1 所示,如果要调查某省总人口中的男性比例,自然不可能去统计总人口数和男性的总人数。常见的方法是进行科学的抽样,抽样所得的男性比例即可近似作为总人口的男性比例。这样做的科学性是由著名的 Hoeffding 不等式 (hoeffding's Inequality) 保证的。
Hoeffding不等式可以保证 “总人口中的男性比例(记作 )” 与 “样本中的男性比例(记作
)” 与 “样本中的男性比例(记作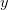 )” 满足以下关系:
)” 满足以下关系:
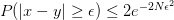
其中  是你可以设定的容忍误差范围,
是你可以设定的容忍误差范围,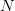 是你的抽样大小。
是你的抽样大小。
Hoeffding不等式告诉我们,当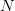 足够大时,“总人口中的男性比例” 与 “样本中的男性比例” 的差值,这个值超出误差范围
足够大时,“总人口中的男性比例” 与 “样本中的男性比例” 的差值,这个值超出误差范围 的概率会非常小。比如你希望误差范围
的概率会非常小。比如你希望误差范围 为0.01,代入Hoeffding不等式计算可得,大约只需要抽样调查5万人即可保证
为0.01,代入Hoeffding不等式计算可得,大约只需要抽样调查5万人即可保证  和
和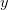 的差值超出
的差值超出
 的概率小于等于0.01%.
的概率小于等于0.01%.
于是我们就可以说,通过抽样统计,可以十分有把握地“预测”总人口的男性比例。
好,理解了人口调查的例子,其实 Hypothesis Set 中只有一个 hypothesis 的情况是完全等价的:
- 我们希望知道模型的预测准确率,就像我们希望知道总人口中的男性比例。
- 既然我们通过科学抽样和Hoeffding不等式的帮助,可以用样本的男性比例去“逼近”总人口的男性比例,当然就可以做到用模型的训练准确率去“逼近”预测准确率。
具体的,只需将 Hypothesis Set 中这个唯一的 hypothesis 记作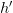 ,对应的上帝真相 (Ground Truth)记作
,对应的上帝真相 (Ground Truth)记作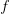 ,然后做两个简单的替换:
,然后做两个简单的替换:
- 将人口统计中的 ”男“ 替换成 “
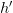 判断正确,即
判断正确,即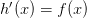 ”
” - 将人口统计中的 ”女“ 替换成 “
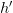 判断错误,即
判断错误,即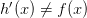 ”
”
图2:
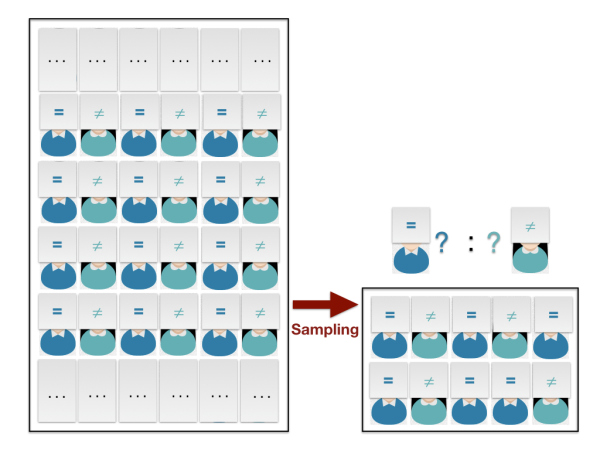
如图 2 所示,替换之后就跟人口统计一样,我们希望知道未知数据上模型的预测准确率,只需科学采样并统计样本数据上的准确率即可。它当然也满足Hoeffding不等式,“在未知数据上预测正确的比例(记作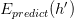 )” 与 “在样本上训练正确的比例(记作
)” 与 “在样本上训练正确的比例(记作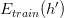 )” 满足以下关系:
)” 满足以下关系:
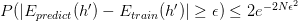
其中 是你可以设定的容忍误差范围,
是你可以设定的容忍误差范围,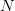 是你的抽样大小。这时我们称:
是你的抽样大小。这时我们称: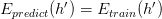 is Probably Approximately Corrent (PAC) 。
is Probably Approximately Corrent (PAC) 。
也就是说,当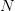 足够大时,“训练准确率” 与 “预测准确率” 的差值,这个值超出误差范围
足够大时,“训练准确率” 与 “预测准确率” 的差值,这个值超出误差范围 的概率会非常小。于是当我们发现模型
的概率会非常小。于是当我们发现模型
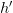 在训练样本上的表现很好时,就可以十分有把握地认为它在“预测未来”时会表现的一样好!
在训练样本上的表现很好时,就可以十分有把握地认为它在“预测未来”时会表现的一样好!
是,上帝是存在的,只要你找到她的影子。
当然,我们都知道人口统计时科学的采样是至关重要的,如果我们抽样的方法不够科学,比如你抽样的都是单一地区或者单一年龄段的样本,那么Hoeffding不等式将不再庇佑你。
机器学习的采样也是一样,本篇后面所有讨论的前提都默认抽样的科学性,保证样本满足独立同分布 (independent and identically distributed, 简写i.i.d.)。关于独立同分布,西瓜书这样解释道:
输入空间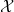 中的所有样本服从一个隐含未知的分布,训练数据所有样本都是独立地从这个分布上采样而得。
中的所有样本服从一个隐含未知的分布,训练数据所有样本都是独立地从这个分布上采样而得。
记住独立同分布(i.i.d)这个名字,因为从今天开始,在机器学习世界里,人们将一次一次无数次地提及它的大名。
3. 第二种情况 —— Hypothesis Set 中存在有限个 hypothesis 的情况
在第一种情况中,我们已经证明了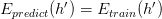 is Probably Approximately Corrent (PAC) 。
is Probably Approximately Corrent (PAC) 。
不过因为 Hypothesis Set 中只有一个 hypothesis 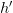 ,所以学习算法并没什么好选的,学到的模型一定就是
,所以学习算法并没什么好选的,学到的模型一定就是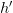 。当学习算法没有选择的空间时,得到一个训练准确率很高的模型几乎是不可能的。就像
PLA 算法如果只有一条线可选,这条线多半在训练数据上的表现是很差的。这时预测能做到跟训练差不多的水准,多半也不是表现的“一样好”,而是表现的”一样差“了。
。当学习算法没有选择的空间时,得到一个训练准确率很高的模型几乎是不可能的。就像
PLA 算法如果只有一条线可选,这条线多半在训练数据上的表现是很差的。这时预测能做到跟训练差不多的水准,多半也不是表现的“一样好”,而是表现的”一样差“了。
所以,让Hypothesis Set 中有许多的 hypothesis,学习算法才有选择的空间挑选到一个准确率较高的 hypothesis 。此时预测表现接近训练表现才是有意义的。
既然如此,那么现在我们就来讨论一下第二种情况,看看当 Hypothesis Set 中存在有限个 hypothesis 时会发生什么。为了便于表达,我们称这种情况为有限假设空间,并假设 Hypothesis Set 中有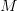 个 hypothesis。
个 hypothesis。
还是先回顾下单个 hypothesis 保证到的情况 —— “ 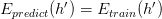 is PAC ” ,即
is PAC ” ,即
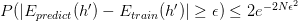
我们前面已经说了,这个公式代表了预测准确率偏离训练准确率的概率很小。但反过来看,它也相当于是说,采样多达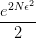 次,平均也会撞到一次超出容忍误差的情况。用人口统计的例子来说就是,每年统计一次,一连统计了5万年,平均也会遇到一次精度超出预期。如果我们把这种情况称为“hypothesis
次,平均也会撞到一次超出容忍误差的情况。用人口统计的例子来说就是,每年统计一次,一连统计了5万年,平均也会遇到一次精度超出预期。如果我们把这种情况称为“hypothesis 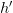 撞了墙”,将
“
撞了墙”,将
“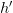 撞了墙的概率” 用
撞了墙的概率” 用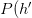 撞墙
撞墙 表示,则有
表示,则有
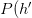 撞墙
撞墙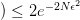
当 Hypothesis Set 有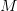 个假设时,任意一个 hypothesis 撞了墙都是我们不希望看到的,因为任何一个 hypothesis 都有可能被学习算法选作最终的模型。所以,现在就让我们看看“任意 hypothesis 撞墙的概率”。
个假设时,任意一个 hypothesis 撞了墙都是我们不希望看到的,因为任何一个 hypothesis 都有可能被学习算法选作最终的模型。所以,现在就让我们看看“任意 hypothesis 撞墙的概率”。
图3:

如图3所示,将“任意 hypothesis 撞墙的概率”记作 P(任意hypothesis撞墙)
- 上图第 1 步:这步很显然,只是将“任意 hypothesis” 用
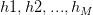 展开。
展开。 - 上图第2步:根据 Union Bound ,很直观的有
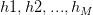 任意一个撞墙的概率小于等于单个hypothesis撞墙的概率总和。
任意一个撞墙的概率小于等于单个hypothesis撞墙的概率总和。 - 上图第3步:单个hypothesis撞墙的概率我们早已知道,
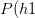 撞墙
撞墙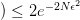 ,
,
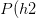 撞墙
撞墙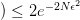 , ... ,
, ... , 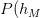 撞墙
撞墙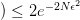 。代入第2步即可。
。代入第2步即可。 - 上图第4步:加和,最终得到任意 hypothesis 撞墙的概率小于等于
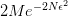 。这意味着当 Hypothesis Set 中有
。这意味着当 Hypothesis Set 中有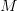 个 hypothesis 时,撞墙的概率变成了只有一个 hypothesis 时的
个 hypothesis 时,撞墙的概率变成了只有一个 hypothesis 时的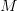 倍。
倍。
这对于机器学习来说仍然是个好消息,因为无论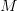 个 hypothesis 中哪个 hypothesis 被学习算法选作最终的模型
个 hypothesis 中哪个 hypothesis 被学习算法选作最终的模型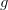 ,只要样本数
,只要样本数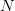 足够大,仍然可以保证
足够大,仍然可以保证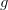 的 “训练准确率” 与 “预测准确率” 的差值,这个值超出误差范围
的 “训练准确率” 与 “预测准确率” 的差值,这个值超出误差范围 的概率会非常小。这时我们称:
的概率会非常小。这时我们称:
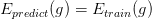 is Probably Approximately Corrent (PAC) 。
is Probably Approximately Corrent (PAC) 。
所以在这种情况下,未来仍然在我们的掌控之中!
4. 下篇预告 —— Hypothesis Set中存在无限个 Hypothesis 的情况
现在已经搞定了单个 hypothesis 以及有限个 hypothesis的情况,离目标只差最后一点 —— Hypothesis Set中存在无限个 hypothesis 的情况。
首先我们回顾下在有限假设空间的情况下得到的的结论:
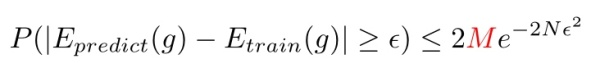
这个公式告诉我们训练准确率和预测准确的差值超出误差的概率会被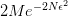 限制住,也就是说无论 Hypothesis Set 的大小
限制住,也就是说无论 Hypothesis Set 的大小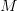 是多少,只要它是有限的,总是可以以足够多的样本将“撞墙概率”限制住。
是多少,只要它是有限的,总是可以以足够多的样本将“撞墙概率”限制住。
可是,一旦 Hypothesis Set 中有无限个 hypothesis,即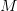 是无穷大,公式右侧的限制就失效了。预测准确率与训练准确率之间的连线被无限大的
是无穷大,公式右侧的限制就失效了。预测准确率与训练准确率之间的连线被无限大的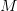 撕裂使得对未来的预测再次陷入迷雾之中。下一篇我们要做的,就是在”无限假设空间“的情况下,再一次试图从无穷大中找到某个天花板,重新将预测未来的希望抓在手里......(未完待续)
撕裂使得对未来的预测再次陷入迷雾之中。下一篇我们要做的,就是在”无限假设空间“的情况下,再一次试图从无穷大中找到某个天花板,重新将预测未来的希望抓在手里......(未完待续)
5. 后记
感谢您的阅读,这里是《写给大家看的机器学习书》,我是八汰。如果您希望收到后续文章的更新,可以考虑关注我。或者关注这个同名专栏,文章将会在您的通知中心推送更新。
祝开心 :)