1. 提要
从这个系列文章的第四篇开始,我们开启了机器学习可行性的讨论。
这是所有机器学习者都要面临的一道考验,当你掌握了机器学习的基本概念,习得了若干个具体的算法,甚至进行了一两个实际问题的实践,无可逃避的,你必将面临这挥之不去的疑问:
由训练数据也就是历史日志学得的模型,真的能在未来的预测中表现的一样好吗?你敢按照从股市历史数据中学到的模型操作真金白银的投资吗?
有的学习者选择了视而不见,有的学习者选择了盲从,他们选择忽视这个机器学习门外石碑上刻着的终极疑问:
为什么可以学习
这个问题的答案隐藏在机器学习的分支——计算学习理论之中,它不仅是机器学习的理论基础,更是一切高楼的基石。如果无法找到这个问题的答案,学习再多的学习算法和模型都将沦为脚下悬空的招式,不得心法,将永远是机器学习半掩大门外的“门外汉”。
而来到这个系列文章第六篇的各位,已经找到了这个问题一半以上的答案,学习完这一篇关于计算学习理论最后的讨论,从此各位跨入机器学习的大门,天地高山,都在脚下。
2. Hypothesis Set 中存在无限个 hypothesis 的情况
这个系列文章将计算学习理论的整个讲解分成三步,在此之间,我们已经搞定了单个 hypothesis 和有限假设空间两种情况,离目标只差最后一步 —— Hypothesis Set 中存在无限个 hypothesis ,即无限假设空间的情况。
首先我们回顾下在有限假设空间的情况下得到的的结论:
<img src="https://pic4.zhimg.com/v2-1ae7db2dbae44f369788b5e1086077ff_b.jpg" data-rawwidth="732" data-rawheight="83" class="origin_image zh-lightbox-thumb" width="732" data-original="https://pic4.zhimg.com/v2-1ae7db2dbae44f369788b5e1086077ff_r.jpg">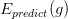 表示预测准确率,
表示预测准确率,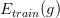 表示训练准确率,
表示训练准确率, 则是可以设定的容忍误差范围。这个公式告诉我们训练准确率和预测准确的差值超出误差的概率会被
则是可以设定的容忍误差范围。这个公式告诉我们训练准确率和预测准确的差值超出误差的概率会被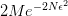 限制住。也就是说无论 Hypothesis Set 的大小
限制住。也就是说无论 Hypothesis Set 的大小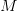 是多少,只要它是有限的,总是可以以足够多的样本数
是多少,只要它是有限的,总是可以以足够多的样本数
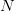 将“撞墙概率”限制住。
将“撞墙概率”限制住。
可是,一旦 Hypothesis Set 中有无限个 hypothesis,即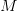 是无穷大,公式右侧的限制就失效了。预测准确率与训练准确率之间的连线被无穷大的
是无穷大,公式右侧的限制就失效了。预测准确率与训练准确率之间的连线被无穷大的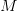 撕裂使得对未来的预测再次陷入迷雾之中。这一篇我们要做的,就是在无限假设空间的情况下,再一次试图从无穷大的虚空之中找到某个天花板,将预测未来的希望重新抓在手里。
撕裂使得对未来的预测再次陷入迷雾之中。这一篇我们要做的,就是在无限假设空间的情况下,再一次试图从无穷大的虚空之中找到某个天花板,将预测未来的希望重新抓在手里。
为了做到这一点,就需要找到某个东西代替无穷大的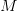 限制住“撞墙概率”。在我们找到它之前,不妨就叫它
限制住“撞墙概率”。在我们找到它之前,不妨就叫它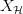 ,我们希望找到这么一个
,我们希望找到这么一个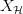 ,使得
,使得
3. 寻找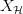 的路上遇到 dichotomy
的路上遇到 dichotomy
有什么方法能在无限假设空间的情况下找到这么一个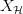 呢。我们还得从这个系列文章唯一讲过的学习算法 PLA (Perceptron Learning Algorithm) 入手。
呢。我们还得从这个系列文章唯一讲过的学习算法 PLA (Perceptron Learning Algorithm) 入手。
读过写给大家看的机器学习书(第三篇)的朋友或许还记得,PLA 的 Hypothesis Set 就属于有无限多个 hypothesis 的情况,其中每个 hypothesis 都可视作一条将平面分隔成两个区域的直线。不过你有没有注意到,代表着 hypothesis 的直线虽然有无限多条,可是线的种类却是有限的!什么意思呢?
我们先来看图1。它展示了当样本数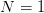 时,PLA 的 hypothesis 无非就只有
时,PLA 的 hypothesis 无非就只有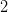 种:
种:
- 一种像图1左那样:线在样本的左边,即判定样本为
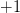 (红圈)。这个时候任意一个 hypothesis,只要它判定样本为
(红圈)。这个时候任意一个 hypothesis,只要它判定样本为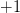 (红圈),那么我们就说这个 hypothesis 跟图1左所示的 hypothesis 是“等效”的。
(红圈),那么我们就说这个 hypothesis 跟图1左所示的 hypothesis 是“等效”的。 - 另一种则像图1右那样:线在样本的右边,即判定样本为
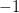 (蓝叉)。同样的,任意一个 hypothesis ,只要它判定样本为
(蓝叉)。同样的,任意一个 hypothesis ,只要它判定样本为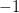 (蓝叉),我们就说这个 hypothesis 跟图1右所示的 hypothesis 是“等效”的。
(蓝叉),我们就说这个 hypothesis 跟图1右所示的 hypothesis 是“等效”的。
于是,在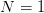 的情况下,无限多的 hypothesis 就这样被归结为“等效”的两种,我们似乎找到了一把从“无限”通向“有限”的钥匙。
的情况下,无限多的 hypothesis 就这样被归结为“等效”的两种,我们似乎找到了一把从“无限”通向“有限”的钥匙。
而这两种 hypothesis,要么将样本判定为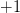 ,要么将样本判定为
,要么将样本判定为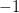 ,任意一种输出就叫做一种 dichotomy,全称为 “PLA 的 Hypothesis Set 在单样本上的两种 dichotomy”。
,任意一种输出就叫做一种 dichotomy,全称为 “PLA 的 Hypothesis Set 在单样本上的两种 dichotomy”。
dichotomy,中文译名“对分”,可能是这个译名实在有点拗口,日常交流时这个词大多就直接用英文,念作 [daɪ'kɑtəmi]。
图1:
<img src="https://pic1.zhimg.com/v2-7acdad704bed2169a94b91c17d7c6294_b.jpg" data-rawwidth="1024" data-rawheight="768" class="origin_image zh-lightbox-thumb" width="1024" data-original="https://pic1.zhimg.com/v2-7acdad704bed2169a94b91c17d7c6294_r.jpg">类似的,图2展示了当样本数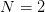 时,PLA 的 hypothesis 一共只有
时,PLA 的 hypothesis 一共只有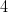 种。
种。
- 一种如图2左上:判定两个样本都是
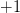 (红圈)。这个时候任意一个 hypothesis,只要它对样本的输出跟图2左上相同,我们就说这个 hypothesis 跟图2左上所示的 hypothesis 是“等效”的。
(红圈)。这个时候任意一个 hypothesis,只要它对样本的输出跟图2左上相同,我们就说这个 hypothesis 跟图2左上所示的 hypothesis 是“等效”的。 - 一种如图2右上:判定一个样本为
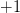 (红圈),另一个为
(红圈),另一个为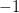 (蓝叉)。这个时候任意一个 hypothesis,只要它对样本的输出跟图2右上相同,我们就说这个 hypothesis 跟图2右上所示的 hypothesis 是“等效”的。
(蓝叉)。这个时候任意一个 hypothesis,只要它对样本的输出跟图2右上相同,我们就说这个 hypothesis 跟图2右上所示的 hypothesis 是“等效”的。 - 一种如图2左下:判定两个样本都是
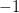 (蓝叉)。这个时候任意一个 hypothesis,只要它对样本的输出跟图2左下相同,我们就说这个 hypothesis 跟图2左下所示的 hypothesis 是“等效”的。
(蓝叉)。这个时候任意一个 hypothesis,只要它对样本的输出跟图2左下相同,我们就说这个 hypothesis 跟图2左下所示的 hypothesis 是“等效”的。 - 一种如图2右下:判定一个样本为
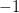 (蓝叉),另一个为
(蓝叉),另一个为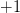 (红圈)。这个时候任意一个 hypothesis,只要它对样本的输出跟图2右下相同,我们就说这个 hypothesis 跟图2右下所示的 hypothesis 是“等效”的。
(红圈)。这个时候任意一个 hypothesis,只要它对样本的输出跟图2右下相同,我们就说这个 hypothesis 跟图2右下所示的 hypothesis 是“等效”的。
也就是说任意 PLA 的 hypothesis,它对样本的输出一定跟图2四种情况中的其中一种相同,于是我们在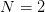 的情况下,也将无限多的 hypothesis 归结为“等效”的4种。用 dichotomy 来描述就是,PLA 的 Hypothesis
Set 在
的情况下,也将无限多的 hypothesis 归结为“等效”的4种。用 dichotomy 来描述就是,PLA 的 Hypothesis
Set 在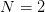 时一共有 4 种 dichotomy。
时一共有 4 种 dichotomy。
这把从“无限”通往“有限”的钥匙似乎更加可信了。
图2:
<img src="https://pic2.zhimg.com/v2-13bad35a824cade26c28ed266b3bf031_b.jpg" data-rawwidth="1024" data-rawheight="768" class="origin_image zh-lightbox-thumb" width="1024" data-original="https://pic2.zhimg.com/v2-13bad35a824cade26c28ed266b3bf031_r.jpg">更一般的,当训练数据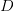 有
有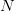 个样本时(
个样本时(
 ),对于任意两个 hypothesis
),对于任意两个 hypothesis 和
和 ,如果它们对这
,如果它们对这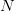 个样本的输出是相同的,即
个样本的输出是相同的,即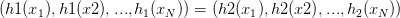 ,那么我们就说
,那么我们就说
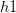 和
和 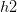 在这
在这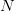 个样本上是“等效”的。它们对这
个样本上是“等效”的。它们对这
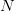 个样本的输出就称为
个样本的输出就称为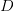 的其中一种 dichotomy。很显然,对于二分类问题(输出要么为
的其中一种 dichotomy。很显然,对于二分类问题(输出要么为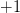 要么为
要么为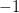 ),任意 Hypothesis Set 对
),任意 Hypothesis Set 对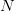 个样本最多有
个样本最多有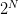 种 dichotomy 。
种 dichotomy 。
4. 寻找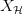 的路上遇到成长函数 (Growth Function)
的路上遇到成长函数 (Growth Function)
经过上面的讨论,我们已经了解到,尽管在无限假设空间的情况下 Hypothesis Set 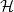 中可能有无限多个 hypothesis,但它们对训练集合
中可能有无限多个 hypothesis,但它们对训练集合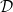 的可能的输出结果是有限的,每种可能的输出就是
的可能的输出结果是有限的,每种可能的输出就是 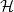 对
对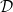 的一种 dichotomy。且当样本数是
的一种 dichotomy。且当样本数是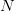 时,最多就只有
时,最多就只有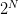 种 dichotomy。如果将训练数据
种 dichotomy。如果将训练数据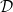 的
的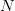 个样本记作
个样本记作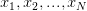 ,将 dichotomy 的数量用符号
,将 dichotomy 的数量用符号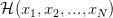 表示,就有:
表示,就有:
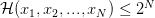
这个时候,就找到了这样的一个值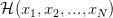 ,它虽然随着
,它虽然随着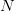 趋向无穷大而趋向无穷大,但是却有着一个确定的上界
趋向无穷大而趋向无穷大,但是却有着一个确定的上界 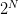 。于是很自然的我们要问,这个有着上界的值能帮助我们限制住“撞墙概率”吗?它是不是就是我们要找的
。于是很自然的我们要问,这个有着上界的值能帮助我们限制住“撞墙概率”吗?它是不是就是我们要找的
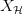 呢?
呢?
还不是!
继续分析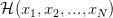 这个值就会发现,用它来表示 dichotomy 的数量有个小小的问题 —— 那就是对于确定的 Hypothesis Set,哪怕样本数
这个值就会发现,用它来表示 dichotomy 的数量有个小小的问题 —— 那就是对于确定的 Hypothesis Set,哪怕样本数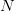 的值固定,
的值固定,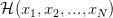 的值也可能随着样本的变化而发生变化。仍然以 PLA 举例:
的值也可能随着样本的变化而发生变化。仍然以 PLA 举例:
- 如图 3 所示,样本数
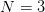 ,这种情况 PLA 的
,这种情况 PLA 的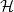 可以做出
可以做出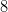 种 dichotomy 。(你能画出对应的 hypothesis 所代表的直线吗?)
种 dichotomy 。(你能画出对应的 hypothesis 所代表的直线吗?) - 如图 4 所示,同样是样本数
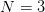 ,这种情况 PLA 的
,这种情况 PLA 的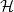 只能做出上半部分的
只能做出上半部分的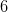 种 dichotomy 。(想一想为什么下半部分的另外
种 dichotomy 。(想一想为什么下半部分的另外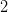 种做不出来?)
种做不出来?)
图3:
<img src="https://pic3.zhimg.com/v2-24018456bd6e31689db0ba13585b978e_b.jpg" data-rawwidth="1024" data-rawheight="768" class="origin_image zh-lightbox-thumb" width="1024" data-original="https://pic3.zhimg.com/v2-24018456bd6e31689db0ba13585b978e_r.jpg">图4:
<img src="https://pic3.zhimg.com/v2-bd6cf4cbfe4023e32e3895de3755d932_b.jpg" data-rawwidth="1024" data-rawheight="768" class="origin_image zh-lightbox-thumb" width="1024" data-original="https://pic3.zhimg.com/v2-bd6cf4cbfe4023e32e3895de3755d932_r.jpg">正因为这样,用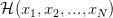 来表示 dichotomy 的数量就会引起一系列的不便。为了消除样本变化带来的影响,人们希望 dichotomy 的数量只与 Hypothesis Set 和 样本数量
来表示 dichotomy 的数量就会引起一系列的不便。为了消除样本变化带来的影响,人们希望 dichotomy 的数量只与 Hypothesis Set 和 样本数量
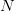 相关,于是创造了另一个专门的概念 —— 成长函数 (Growth Function),来表示 dichotomy 的数量。
相关,于是创造了另一个专门的概念 —— 成长函数 (Growth Function),来表示 dichotomy 的数量。
成长函数 (Growth Function) 的定义非常简单,对于具体的 Hypothesis Set 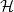 ,成长函数 (Growth Function) 就等于样本数等于
,成长函数 (Growth Function) 就等于样本数等于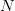 时
时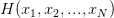 的最大值。将成长函数 (Growth Function) 记作
的最大值。将成长函数 (Growth Function) 记作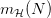 ,就可以写成:
,就可以写成:
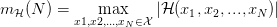
于是,用成长函数 (Growth Function) 来表示 dichotomy 的数量,就解决了之前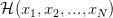 所存在的问题。对于确定的
所存在的问题。对于确定的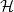 ,无论样本怎么变化,只要样本数
,无论样本怎么变化,只要样本数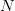 确定,最大的 dichotomy 数量(也就是成长函数的取值)就是确定的。比如对于PLA,
确定,最大的 dichotomy 数量(也就是成长函数的取值)就是确定的。比如对于PLA,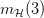 就等于 8 (6和8的最大值是8)。
就等于 8 (6和8的最大值是8)。
值得特别提出的是,成长函数 (Growth Function) 是 Hypothesis Set 本身的性质,它代表了 Hypothesis Set 最多能将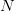 个样本分成多少种 dichotomy,也就是我们所说的
个样本分成多少种 dichotomy,也就是我们所说的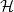 中最多有几种 hypothesis。显然的,成长函数跟
中最多有几种 hypothesis。显然的,成长函数跟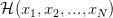 一样,也有着确定的上界
一样,也有着确定的上界
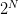 ,即
,即
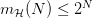
那么是不是说此时的成长函数就是我们要找的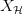 呢?
呢?
仍然不够理想!
我们不妨试着如下图第①步所示,将成长函数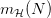 当做
当做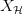 代入公式。然后,如下图第②步所示,将成长函数的上界
代入公式。然后,如下图第②步所示,将成长函数的上界 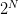 代入。最后,如下图第③步所示将公式的右边变换成分数表示。
代入。最后,如下图第③步所示将公式的右边变换成分数表示。
图5:
<img src="https://pic4.zhimg.com/v2-ade2a0775605d211c25d71095cad38fb_b.jpg" data-rawwidth="819" data-rawheight="554" class="origin_image zh-lightbox-thumb" width="819" data-original="https://pic4.zhimg.com/v2-ade2a0775605d211c25d71095cad38fb_r.jpg">这个时候公式右侧的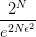 是不是一个理想的上界,可以将“撞墙概率”限制住呢?要回答这个问题,需要大家稍稍的回忆微积分课程中关于“极限和无穷”的知识:
是不是一个理想的上界,可以将“撞墙概率”限制住呢?要回答这个问题,需要大家稍稍的回忆微积分课程中关于“极限和无穷”的知识:
- 首先看分子部分,当样本数
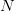 趋向正无穷时,很显然
趋向正无穷时,很显然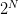 是趋向正无穷的,即
是趋向正无穷的,即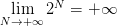 。
。 - 再看分母部分,当样本数
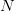 趋向正无穷时,
趋向正无穷时,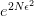 也同样趋向正无穷,即
也同样趋向正无穷,即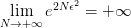 。
。
那么两个正无穷是否可以“比大小”呢?当然可以,“函数极限及无穷”部分的知识(参考资料1 参考资料2 参考资料3)告诉我们:两个函数
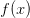 和
和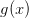 ,
,
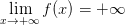 ,
,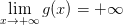 :
:
如果,则称
是
的低阶无穷大。也就是我们一般所理解的
比
“小”。
如果
,则称
是
的高阶无穷大。也就是我们一般所理解的
比
“大”。
在图5最后一个公式所示的情况下,我们当然希望分子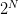 是分母
是分母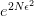 的低阶无穷大(也就是希望分子比分母“小”),因为只有这样才会有
的低阶无穷大(也就是希望分子比分母“小”),因为只有这样才会有 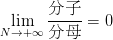 ,才意味着我们可以通过增大样本数
,才意味着我们可以通过增大样本数
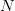 控制住“撞墙概率”,使得预测准确率和训练准确率的差值超出误差的概率尽可能的小。不过很遗憾,此时成长函数的上界
控制住“撞墙概率”,使得预测准确率和训练准确率的差值超出误差的概率尽可能的小。不过很遗憾,此时成长函数的上界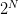 并不是
并不是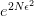 的低阶无穷大,要想达到我们的希望,成长函数应该有一个比
的低阶无穷大,要想达到我们的希望,成长函数应该有一个比 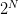 还要“小”的上界函数。它需要是
还要“小”的上界函数。它需要是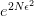 的低阶无穷大。只有这样,才能最终将“撞墙概率”限制住,才能重新将预测准确率和训练准确率牢牢地拴在一起。
的低阶无穷大。只有这样,才能最终将“撞墙概率”限制住,才能重新将预测准确率和训练准确率牢牢地拴在一起。
5. 寻找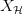 的路上遇到 Break Point
的路上遇到 Break Point
那么成长函数有没有可能找到一个更“小”的上界,使得它是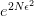 的低阶无穷大呢?我们仍然需要在 PLA 中寻找蛛丝马迹。
的低阶无穷大呢?我们仍然需要在 PLA 中寻找蛛丝马迹。
在前面的例子中,讨论过了 PLA 的 Hypothesis Set 的 3 种情况:
- 当样本数
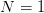 时,最多有
时,最多有 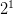 种 dichotomy,即成长函数
种 dichotomy,即成长函数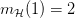 。
。 - 当样本数
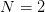 时,最多有
时,最多有 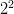 种 dichotomy,即成长函数
种 dichotomy,即成长函数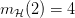 。
。 - 当样本数
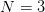 时,最多有
时,最多有 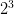 种 dichotomy,即成长函数
种 dichotomy,即成长函数 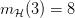 。
。
可是如果继续看样本数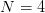 的情况,就会发现此时最多只能做出 14 种 dichotomy,达不到
的情况,就会发现此时最多只能做出 14 种 dichotomy,达不到 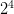 种。如图6所示的这两种 dichotomy,PLA 的 Hypothesis Set 做不出来。
种。如图6所示的这两种 dichotomy,PLA 的 Hypothesis Set 做不出来。
不仅如此,一旦从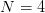 开始 PLA 的 Hypothesis Set 做不出
开始 PLA 的 Hypothesis Set 做不出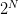 种 dichotomy,可以证明对于任意样本数
种 dichotomy,可以证明对于任意样本数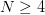 ,它都再做不出
,它都再做不出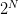 dichotomy。这个对我们意义重大的点
dichotomy。这个对我们意义重大的点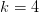 就称为 PLA Hypothesis Set 的 Break Point 。
就称为 PLA Hypothesis Set 的 Break Point 。
图6:
<img src="https://pic3.zhimg.com/v2-6632478eeef3f13bbff1bc1f114f33fa_b.jpg" data-rawwidth="1024" data-rawheight="768" class="origin_image zh-lightbox-thumb" width="1024" data-original="https://pic3.zhimg.com/v2-6632478eeef3f13bbff1bc1f114f33fa_r.jpg">更一般的,任意 Hypothesis Set,如果存在某个值
,使得
对所有可能的
个样本都无法做出
种 dichotomy (即
),那么最小的那个
就称为这个 Hypothesis Set 的 Break Point。
Break Point 对我们的意义是重大的,它意味着只要某个 Hypothesis Set 存在 Break Point 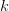 ,那么从
,那么从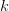 开始成长函数的值就会比
开始成长函数的值就会比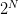 小。小到什么程度呢?
小。小到什么程度呢?
小到美梦成真!!!
事实上,只要 Hypothesis Set 存在 Break Point 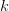 ,成长函数就满足一个“更小”的上界
,成长函数就满足一个“更小”的上界
1:
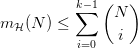
这个上界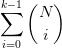 是一个多项式函数,满足我们寻找的理想上界的条件:是
是一个多项式函数,满足我们寻找的理想上界的条件:是
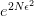 的低阶无穷大。于是再次参照图10将成长函数和它的上界代入,所得如图7所示:
的低阶无穷大。于是再次参照图10将成长函数和它的上界代入,所得如图7所示:
图7:
<img src="https://pic3.zhimg.com/v2-1dfbad70a1c51cbc83f443c1a37c3876_b.jpg" data-rawwidth="759" data-rawheight="366" class="origin_image zh-lightbox-thumb" width="759" data-original="https://pic3.zhimg.com/v2-1dfbad70a1c51cbc83f443c1a37c3876_r.jpg">第二个公式的右侧满足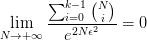 ,也就是说当
,也就是说当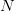 趋向正无穷时,
趋向正无穷时,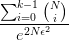 趋向于
趋向于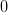 。所以就可以通过增大样本数
。所以就可以通过增大样本数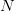 限制住“撞墙概率”,使得预测准确率和训练准确率的差值超出误差的概率尽可能的小。
限制住“撞墙概率”,使得预测准确率和训练准确率的差值超出误差的概率尽可能的小。
不过这里还有一个小小的伏笔,细心的同学可能有注意到在图5的第①步和图7中,都用了一个虚线的箭头。因为事实上并不能简单用成长函数去替换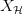 ,在无限假设空间下训练准确率和预测准确率真正满足的公式长这样:
,在无限假设空间下训练准确率和预测准确率真正满足的公式长这样:
图8:
<img src="https://pic4.zhimg.com/v2-1151ebfd5ea79bfc3a6a2e5478eaf90b_b.jpg" data-rawwidth="801" data-rawheight="104" class="origin_image zh-lightbox-thumb" width="801" data-original="https://pic4.zhimg.com/v2-1151ebfd5ea79bfc3a6a2e5478eaf90b_r.jpg">我们发现这个公式除了代入了成长函数,还多出了几个蓝色的常数。
这就是大名鼎鼎的 Vapnik-Chervonenkis Bound, 简称 VC Bound 。Vapnik 和 Chervonenkis 在1971年提出并完整地证明了它。如果对这个公式的数学证明和证明技巧感兴趣,或者希望了解那几个多出来的蓝色常数是怎么来的,可以参见 Bapnik and Chervonenkis 1971 。不过在这里,更重要的是理解 VC Bound 对于我们的非凡意义:
VC bound 保证了“撞墙概率”的上界与成长函数之间的关系!有了 VC bound 的庇佑,从此只要学习算法的 Hypothesis Set 存在 Break Point,就可以将成长函数的理想上界代入其中(如下图所示)。
于是在无限假设空间的情况下,只要样本数足够大,预测准确率偏离训练准确率的概率也可以变得足够小。
图9:
<img src="https://pic3.zhimg.com/v2-e3a5e18ab3fb59a9a59f385afbbd8e52_b.jpg" data-rawwidth="783" data-rawheight="198" class="origin_image zh-lightbox-thumb" width="783" data-original="https://pic3.zhimg.com/v2-e3a5e18ab3fb59a9a59f385afbbd8e52_r.jpg">就这样,在无限假设空间中,我们一路走来,遇到了dichotomy,遇到了Growth Functioin,遇到了Break Point,最后终于在 VC Bound 的帮助下找到了梦寐以求的天花板,现在我们真的可以说:
由训练数据学得的模型,真的 (PAC) 能在未来的预测中表现的一样好!
现在的你,敢跟着机器学习投资了吗?:)
6. 对机器学习模型有一个更高层次的理解 —— VC Dimension
关于计算学习理论的讨论进行到这里,似乎已经可以告一段落,毕竟我们已经回答了机器学习“为什么可以学习”这个终极的疑问。不过如果你仍然对机器学习模型的理解有着更高的期待,不妨再与我前行一段。Vapnik 和 Chervonenkis 两位科学家除了 VC bound 之外,还有一份宝贵的财富,要送给每一个机器学习道路上的门徒。
那就是 VC Dimension
6.1 什么是 VC Dimension
要说清楚 VC Dimension 是什么,还得从前面讲过的 Break Point 说起。
我们首先引入一个新词儿——shatter(中文译作”打散“):
对于大小为的样本集合
,如果 Hypothesis Set
可以做出所有可能的
种 dichotomy,则称这
个样本能被 Hypothesis Set
shatter,或者
shatter 了这
个样本。
现在我们用 shatter 来重新描述 Break Point,Break Point 指的就是这样一个”点“:从样本数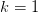 开始数数,
开始数数,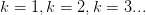 ,数到的的第一个无法被 Hypothesis Set shatter 的"点"就是 Hypothesis Set 的 break point。当然需要强调的是,这里我们说第一个无法被 shatter 的”点“,指的是任意
,数到的的第一个无法被 Hypothesis Set shatter 的"点"就是 Hypothesis Set 的 break point。当然需要强调的是,这里我们说第一个无法被 shatter 的”点“,指的是任意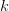 个样本都无法被 shatter。比如像 PLA 那样,在
个样本都无法被 shatter。比如像 PLA 那样,在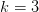 时,图3所示的3个样本可以被shatter,图4所示的3个样本不能被shatter,那就不认为这个“点”不能被
shatter。直到数到
时,图3所示的3个样本可以被shatter,图4所示的3个样本不能被shatter,那就不认为这个“点”不能被
shatter。直到数到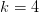 时,任意4个样本都不能被shatter,所以我们说
时,任意4个样本都不能被shatter,所以我们说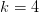 才是第一个不能被shatter的“点”,PLA 的 Break Point 等于4。
才是第一个不能被shatter的“点”,PLA 的 Break Point 等于4。
好,现在我们要换个角度来看,如果说 Break Point 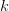 是第一个无法被 Hypothesis Set
是第一个无法被 Hypothesis Set 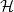 所 shatter 的“点”,那么
所 shatter 的“点”,那么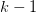 就是最后一个可以被
就是最后一个可以被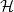 所 shatter 的"点",而
所 shatter 的"点",而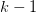 这个"点"就是我们所说的 VC Dimension,中文译作 VC维。(同样值得强调的,这里说
这个"点"就是我们所说的 VC Dimension,中文译作 VC维。(同样值得强调的,这里说
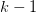 这个“点”可以被 shatter,不需要做到任意
这个“点”可以被 shatter,不需要做到任意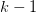 样本都可以被 shatter。只需某
样本都可以被 shatter。只需某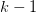 个样本可以被 shatter,我们就说
个样本可以被 shatter,我们就说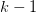 这个“点”可以被 shatter)以 PLA 为例,
这个“点”可以被 shatter)以 PLA 为例,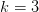 是最后一个可以被其 Hypothesis Set 所 shatter 的“点",所以
PLA Hypothesis Set 的 VC Dimension 就等于 3。
是最后一个可以被其 Hypothesis Set 所 shatter 的“点",所以
PLA Hypothesis Set 的 VC Dimension 就等于 3。
综上,
Break Point 是第一个无法被 Hypothesis Set 所 shatter 的“点” 。
VC Dimension 是最后一个可以被 Hypothesis Set 所 shatter 的“点”。
当然,跟成长函数一样,Break Point 和 VC Dimension 也都属于 Hypothesis Set 本身的性质。不同的 Hypothesis Set 有其各自的 Break Point 和 VC Dimension 。
6.2 VC Dimension 的 4 点馈赠
有的同学可能感到疑惑,这个 VC Dimension 不就是 Break Point 减去 1 吗?那跟 Break Point 有什么区别呢?不要急,有的时候看待事物的角度发生一点点变化,所能看到的东西就会有质的飞跃。VC Dimension 给以我们的就是这样一个全新的理解机器学习模型及其性质的的视角。
VC Dimension 至少在以下4点给以了我们更高的视角,让我们能够对机器学习模型有个更高层次的理解:
第 1 点馈赠:
毫无疑问的,只要某个 Hypothesis Set 存在 VC Dimension,就一定有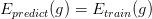 is Probably Approximately Corrent (PAC) 。也就是说由训练数据学得的模型,真的 (PAC) 能在未来的预测中表现的一样好。这是之前 VC Bound 就已经告诉我们了的。
is Probably Approximately Corrent (PAC) 。也就是说由训练数据学得的模型,真的 (PAC) 能在未来的预测中表现的一样好。这是之前 VC Bound 就已经告诉我们了的。
第 2 点馈赠:
VC Dimension 越大,样本复杂度 (sample complexity) 就越高!
你是否注意到图9中的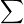 符号上的
符号上的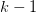 ,它不就是 VC Dimension吗?我们将
,它不就是 VC Dimension吗?我们将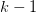 标出如下图图10所示,可以发现 VC Dimension 越大,“
标出如下图图10所示,可以发现 VC Dimension 越大,“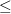 ”号右侧的值就越大,此时如果还希望维持“撞墙概率”不变,就需要更大的样本数
”号右侧的值就越大,此时如果还希望维持“撞墙概率”不变,就需要更大的样本数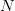 。我们称这种情况为:
。我们称这种情况为:
VC Dimension 越大,样本复杂度 (sample complexity) 就越高。
图10:
<img src="https://pic1.zhimg.com/v2-5c3156aeba605acc51c60bdf57955754_b.jpg" data-rawwidth="902" data-rawheight="264" class="origin_image zh-lightbox-thumb" width="902" data-original="https://pic1.zhimg.com/v2-5c3156aeba605acc51c60bdf57955754_r.jpg">第 3 点馈赠:
VC Dimension 越大,模型的”表达“能力就越强:
VC Dimension 的定义告诉我们,它是最后一个可以被 shatter 的“点”,换句话也可以说,在样本数小于等于 VC Dimension 时, Hypothesis Set 可以“表达”所有可能的样本输出情况。这就是说 VC Dimension 越大,就意味着 Hypothesis Set 的”表达“能力就越强。
又因为最终学得的模型是从 Hypothesis Set 中挑选的最优的那个 hypothesis,不妨认为学得的模型体现的就是 Hypothesis Set 的特点和性质,所以在日常交流中常常就说:
VC Dimension 越大,模型的”表达“能力就越强。
- 第4点馈赠: VC Dimension 是预测准确率优化中的矛盾点
如果把第3点馈赠和第2点馈赠结合起来一起看,似乎 VC Dimension 代表了某种矛盾:
第3点告诉我们 VC Dimension 越大,模型的”表达“能力就越强,但同时第2点又说这会造成“撞墙概率”变大。如果要想维持一定的”撞墙概率“,就需要付出更多的训练样本的代价。
然而在实际工作中,训练样本的获取和数量往往受限于现实的情况,这时 VC Dimension 所代表的矛盾会转移到另一个我们更关心的问题上——预测准确率。VC Dimension 会在预测准确率上表现出怎样的矛盾呢?这需要基于图10所示公式,对训练准确率和预测准确率的接近程度做进一步的推导。这里暂且让我们忽略具体的推导过程,直接给出推导的结果如下图图11所示:
图11
<img src="https://pic1.zhimg.com/v2-0fd30f6b5e683ffe37693613e5f21978_b.jpg" data-rawwidth="1021" data-rawheight="340" class="origin_image zh-lightbox-thumb" width="1021" data-original="https://pic1.zhimg.com/v2-0fd30f6b5e683ffe37693613e5f21978_r.jpg">从图11中可以看到,预测准确率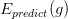 主要受到两个因素的影响:训练准确率
主要受到两个因素的影响:训练准确率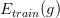 ,还有
,还有 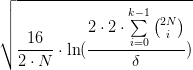 这个值:
这个值:
- 首先,预测准确率
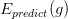 一定大于等于训练准确率
一定大于等于训练准确率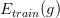 减去
减去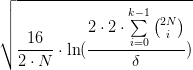 这个值。
这个值。 - 同时,预测准确率
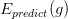 一定小于等于训练准确率
一定小于等于训练准确率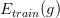 加上
加上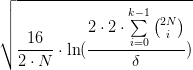 这个值。
这个值。
当然,图11所示公式有个前提条件:只有当训练样本数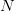 足够大时,才能以足够大的概率
足够大时,才能以足够大的概率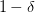 保证图11中的这个值
保证图11中的这个值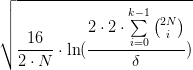 足够小,进而保证预测准确率
足够小,进而保证预测准确率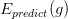 和训练准确率
和训练准确率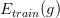 很接近。
很接近。
详细的推导证明我写在附录1供感兴趣的同学参考,这里更重要的是理解 VC Dimension 在预测准确率上表现出的矛盾:
- 从图11公式中可以看到,VC Dimension 越大,
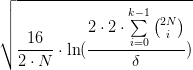 就越大。预测准确率
就越大。预测准确率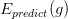 就会越偏离训练准确率
就会越偏离训练准确率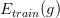 。从这个角度来说,我们希望获得表现更好的预测准确率,应该让 VC Dimension 越小越好。
。从这个角度来说,我们希望获得表现更好的预测准确率,应该让 VC Dimension 越小越好。 - 但另一方面从“第3点馈赠”我们知道了,VC Dimension 越大就说明模型的“表达”能力越强,对训练数据的拟合就越好,学到的
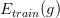 就越大。从这个角度上来说,我们希望获得更优的预测准确率,应该让 VC Dimension 越大越好。
就越大。从这个角度上来说,我们希望获得更优的预测准确率,应该让 VC Dimension 越大越好。
这就是 VC Dimension 在预测准确率上所表现出的矛盾,我们最终希望获得的是更好的预测表现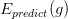 ,然而一味的选择 VC Dimension 更大即更复杂的模型虽然可以让训练准确率
,然而一味的选择 VC Dimension 更大即更复杂的模型虽然可以让训练准确率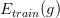 更好,却同时会导致
更好,却同时会导致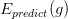 偏离
偏离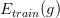 的程度变大。也就是说,如果我们希望获得更好的预测表现,并不能一味地追求更大的 VC Dimension,模型复杂度也并非越高越好,控制和选择合适的 VC Dimension 是机器学习算法设计非常重要的技巧。
的程度变大。也就是说,如果我们希望获得更好的预测表现,并不能一味地追求更大的 VC Dimension,模型复杂度也并非越高越好,控制和选择合适的 VC Dimension 是机器学习算法设计非常重要的技巧。
(如果你对 VC Dimension 所引出的矛盾的理解仍然有所迷惑,或许可以参考附录2中 单 hypothesis 和有限假设空间两种情况的对比)。
7. 课后习题和一则招聘
7.1. 课后习题
站在巨人的肩膀上,我努力让这个主题的写作冲击史上最好的计算学习理论的讲解。是的,我把“之一”都去掉了。
这并不是我企图狂妄的自夸,而是曾经当我自己希望了解“机器为什么可以学习”的时候,在我还不懂什么是成长函数、VC Dimension的时候,当我希望学习计算学习理论的时候,并没有在互联网上找到能够帮助人们“从不知到懂得”的文字资料。
在我看来,计算学习理论的定义是不重要的,重要的告诉人们它试图回答的是个什么样的疑问。成长函数和Break Point的定义是不重要的,重要的是它们为何引出。甚至什么是 VC Dimension 也不重要,重要的是理解它所打开的新视野。
如果一个事情的讲解只能让本来就懂的人频频点头,是讲解者的失败。如果一篇文章的脉络让好奇者越发迷惑,是写作者的无能。
最后,不如就把我很早之前就看到过的一个知乎问题作为计算学习理论的课后习题。问题是:
如何通俗的理解机器学习中的VC维、shatter和break point?——点这里做作业:)
我第一次看到这个问题的时候还不知道什么是VC维度,不理解它为何诞生,有什么用。今天我终于用三篇文章解答了当时的我的所有疑惑,不如,你也试试。
此外,如果你不介意让我知道你的回答是《写给大家看的机器学习书》的习题解答,可以在答案里加上标签 —— #写给大家看的机器学习书的课后习题——某某某的回答#。我会看到并附到文章的后面。
7.2 一则招聘
最后,我所在的阿里巴巴个性化推荐算法团队正在一年一度的招人中。如果您在个性化推荐、计算广告、机器学习方面有过扎实的经历,或者具有非凡的才华、激情和学习力,非常期待与您成为伙伴,可将您的简历发至我的邮箱:hancyxhx@gmail.com。目前社招及2018年应届生的实习岗位招聘均在进行中。
我们团队是阿里巴巴最优秀的算法团队之一,曾拿下2015双十一CEO大奖,手机淘宝用户广泛的产品——有好货、每日好店、猜你喜欢均是出自我们团队之手的用户端产品的作品,淘宝各大大促节日、购物链路的算法产品都有我们的参与、驱动和影响。这个组全是A Players,如果你也是A Player却不知道与一群有才华的伙伴一同做事是种怎样的体验,我觉得你最好不要错过它。
再次感谢您的阅读,这里是《写给大家看的机器学习书》,我是八汰。如果您希望收到后续文章的更新,可以考虑关注我。或者关注这个同名专栏,文章将会在您的通知中心推送更新。
祝开心 :)
8. 附录
8.1 附录1
图10公式到图11公式的推导如下:
图10:
<img src="https://pic1.zhimg.com/v2-5c3156aeba605acc51c60bdf57955754_b.jpg" data-rawwidth="902" data-rawheight="264" class="origin_image zh-lightbox-thumb" width="902" data-original="https://pic1.zhimg.com/v2-5c3156aeba605acc51c60bdf57955754_r.jpg">
图11
<img src="https://pic1.zhimg.com/v2-0fd30f6b5e683ffe37693613e5f21978_b.jpg" data-rawwidth="1021" data-rawheight="340" class="origin_image zh-lightbox-thumb" width="1021" data-original="https://pic1.zhimg.com/v2-0fd30f6b5e683ffe37693613e5f21978_r.jpg">首先,图10说的是
- 当训练样本足够大时(
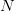 足够大),预测准确率偏离训练准确率大于等于误差
足够大),预测准确率偏离训练准确率大于等于误差 的概率(公式左侧的概率),可以是一个足够小的值 (即
的概率(公式左侧的概率),可以是一个足够小的值 (即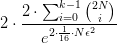 )。
)。
我们只需稍稍换个角度来理解这个公式,完全可以说
- 当训练样本足够大时(
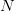 足够大),预测准确率偏离训练准确率小于等于误差
足够大),预测准确率偏离训练准确率小于等于误差 的概率,可以是一个足够大的值(即
的概率,可以是一个足够大的值(即 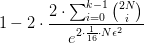 )。这个变换只对图10的公式作一点点改变,写出如图12所示:
)。这个变换只对图10的公式作一点点改变,写出如图12所示:
图12
<img src="https://pic4.zhimg.com/v2-c2c24940d2bd048563514a0ca75ff31f_b.jpg" data-rawwidth="955" data-rawheight="270" class="origin_image zh-lightbox-thumb" width="955" data-original="https://pic4.zhimg.com/v2-c2c24940d2bd048563514a0ca75ff31f_r.jpg">紧接着,因为我们希望分析的是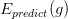 跟
跟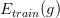 还有 VC Dimension的关系,于是简单的做个变化如下图13所示:
还有 VC Dimension的关系,于是简单的做个变化如下图13所示:
图13:
<img src="https://pic3.zhimg.com/v2-7a48b8080d26a3916c5762c435313baa_b.jpg" data-rawwidth="975" data-rawheight="177" class="origin_image zh-lightbox-thumb" width="975" data-original="https://pic3.zhimg.com/v2-7a48b8080d26a3916c5762c435313baa_r.jpg">最后,将变换得到的 代入图12公式,就得到了下面这个公式(图14),进而推得图11所示结论!
代入图12公式,就得到了下面这个公式(图14),进而推得图11所示结论!
图14:
<img src="https://pic2.zhimg.com/v2-9b4ef3243a0413d4aee924c0fec00c4d_b.jpg" data-rawwidth="854" data-rawheight="229" class="origin_image zh-lightbox-thumb" width="854" data-original="https://pic2.zhimg.com/v2-9b4ef3243a0413d4aee924c0fec00c4d_r.jpg">8.2 附录2
VC Dimension 是预测准确率优化中的矛盾点,其实非常类似 “单hypothesis” 和 “有限假设空间” 两种情况的对比。画图如图15所示,帮助更好的理解:
图15的左侧列出了Hypothesis Set 中只有一个 hypothesis 的情况,这种情况下“撞墙概率”较小(好处),预测准确率可以表现的跟训练准确率“一样好”。但是正如第五篇第3节开头所说,这个时候,因为 Hypothesis Set 中只有一个 hypothesis 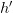 ,所以学习算法并没什么好选的,学到的模型一定就是
,所以学习算法并没什么好选的,学到的模型一定就是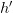 。当学习算法没有选择的空间时,得到一个训练准确率很高的模型几乎是不可能的。就像 PLA 算法如果只有一条线可选,这条线多半在训练数据上的表现是很差的。这时预测能做到跟训练差不多的水准,多半也不是表现的“一样好”,而是表现的”一样差“了(坏处)。
。当学习算法没有选择的空间时,得到一个训练准确率很高的模型几乎是不可能的。就像 PLA 算法如果只有一条线可选,这条线多半在训练数据上的表现是很差的。这时预测能做到跟训练差不多的水准,多半也不是表现的“一样好”,而是表现的”一样差“了(坏处)。
所以,让 Hypothesis Set 中有许多的 hypothesis,学习算法才有选择的空间挑选到一个准确率较高的 hypothesis 。此时预测表现接近训练表现才是有意义的。所以在图15的右侧我们可以看到,Hypothesis Set 有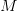 个
hypothesis 让学习算法有了选择的空间,就更可能选到一个在训练数据上表现得更好的 hypothesis(好处)。但是撞墙概率却增大了
个
hypothesis 让学习算法有了选择的空间,就更可能选到一个在训练数据上表现得更好的 hypothesis(好处)。但是撞墙概率却增大了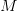 倍(坏处)。
倍(坏处)。
图15
<img src="https://pic1.zhimg.com/v2-ffb8926ca5aaeb47ea7eadfc2a79b650_b.jpg" data-rawwidth="862" data-rawheight="473" class="origin_image zh-lightbox-thumb" width="862" data-original="https://pic1.zhimg.com/v2-ffb8926ca5aaeb47ea7eadfc2a79b650_r.jpg">类似15展示的“单hypothesis” 和 “有限假设空间” 两种情况的对比,现在你能自己说出并理解图16所展示的“VC Dimension较小”和“VC Dimension较大”的对比了吗?
图16:
<img src="https://pic3.zhimg.com/v2-73821368301ace239ca41df034e7d5aa_b.jpg" data-rawwidth="860" data-rawheight="429" class="origin_image zh-lightbox-thumb" width="860" data-original="https://pic3.zhimg.com/v2-73821368301ace239ca41df034e7d5aa_r.jpg">- www.cs.rpi.edu/~magdon/cou… ↩
[^refmaterial]: www.cs.rpi.edu/~magdon/cou…