大家好,我是宅男潇涧,目前是一名鹅厂移动客户端开发工程师。特别感谢小桦哥邀请我为《Android面试指南》小专栏写一篇面试心得,原本的要求是写一篇“对自己部门的面试题深度剖析”,但我本人刚毕业一年多一点(中间还跳槽过一次),虽然也做过面试官,但是更多时候是“面试者”。思来想去,我觉得我还是写一篇侧重算法面试相关的总结会比较好,这样既不太容易和小专栏中其他作者的内容相冲突,也非常适合Android开发求职者的面试需要,小桦哥也欣然同意了。我既不是ACMer,也不是算法牛人,所以本文并不是要说什么高深的算法,而只是从算法面试的角度,侧重分享算法基础知识和算法面试的总结,如果把这些基础打扎实了,应付一般的Android开发岗位的算法面试应该是绰绰有余的 😜
这里简单说下我的面试经历吧。我是在2015年参与到激烈的互联网秋招中的,当年校招头等大事就是“阿里缩招”事件,在西溪园区实习了两个月之后我很不幸地拥抱了变化。9月份回到学校之后我就开始投递简历,后来陆续拿到了腾讯、华为、美团、魅族、360、京东、爱奇艺、完美、猿题库等公司的offer。最后我选择了魅族的offer,在魅族的Flyme核心系统组工作了约半年后,我换了份工作,来到了深圳鹅厂,现在差不多快有一年鹅龄了。那年我写了篇稿子“阿里宝宝漫漫求职路”,意外火了,后来在朋友的建议下,我删了那篇稿子中的面试内容,只留下自己当年准备面试时写下的知识总结,感兴趣可以去看下AndroidInterviews,里面的总结加上我自己博客中的一些读书笔记基本上涵盖了大部分Android基础知识和常见面试题。灰常建议你看下,也许看完了你就是“offer收割机”咯 😉
好了,言归正传吧,下面的内容我主要分为三部分,第一部分是算法基础知识总结,这部分的内容相对多些;第二部分是算法面试经验分享,这部分的内容是和实际算法面试有关的经验;最后一部分是附加的一些面试经验分享,希望对大家求职之路能有所帮助。
1. 算法基础知识总结
俗话说,“不积跬步,无以至千里”,要想搞定算法面试,首先要扎实算法基础。
算法基础知识总结这部分主要有以下几个内容:常见的数据结构及其实现、算法时间复杂度的计算以及常见的算法思想,其中常见的算法思想中有递归、分治、贪心、动规等等。
很显然,一篇文章是不可能将所有算法基础知识都整理出来的,下面我们主要从算法面试的角度依次谈谈这些算法基础知识,很多其他的算法例如图中的算法或者算法思想例如回溯、分支限界等都不在本文中介绍,这部分细节可以参考阅读数据结构与算法设计专栏。
2014年春,我在学校里修了算法分析这门课,断断续续看了大半本《算法导论》。2014年夏,我坐在寝室里读完了《Python Algorithms》这本书。后来,我在自己的博客中写了《Python数据结构与算法设计》系列的文章,总共约十几篇,当时被微博大V Google谷歌爱好者 转发并赐新名,“码农与蛇的故事”,我挺喜欢这个名字,当然,更值得欢喜的是当时个人博客也首次迎来了那么大的访问量 😝
为了写作本文,我把自己的那个系列文章大致读了一遍(好多知识连我寄己都忘了😂),从算法基础知识的角度来看,内容还是比较完备的,只是这个系列在当时写作的时候并没有把握好算法基础知识体系的结构和文章之间的衔接,所以我最近重新整理了一遍,并特意为此创建了一个小专栏《数据结构与算法设计专栏》。如果你看完本文之后对这个系列特别感兴趣的话可以考虑订阅这个小专栏,如果只是一般感兴趣的话可以直接阅读个人博客中原来的那个 系列,内容大致相同,欢迎订阅小专栏以表赞助 😋
1.1 常见的数据结构及其实现
众所周知,数据结构是算法的基石,如果不懂二叉堆这个数据结构怎么写得出堆排序算法呢?
常见的数据结构主要有数组、链表、栈、队列、二叉堆、树、图等,其中栈和队列的题目经常出现在笔试试卷中,而且实际算法面试中二叉堆和图考得很少,经常出现的是数组、链表和二叉树这几种数据结构类型的题目。
(1) 数组虽然是最基础的数据结构,但是能考的东西却非常多,例如最常见的排序算法、找数组中第k大的数字、找两个有序数组的中位数等
[我的面试经历:美团二面遇到合并排序,友盟实习生面试二面遇到找两个有序数组的中位数]
(2) 链表因其特殊的结构也是常考点,例如反转链表、链表元素排序、合并两个有序链表、判断链表是否有环、有环的话环的起点在哪里等
[我的面试经历:腾讯实习生笔试题遇到判断链表是否有环]
(3) 二叉树由于其天然的递归结构,是最适合考查递归思想的数据结构,例如判断二叉树是否平衡、判断二叉树是否相同、判断二叉树是否对称等
[我的面试经历:神马实习生一面遇到判断二叉树是否是平衡二叉树]
(4) 栈和队列也是很重要的数据结构,但是它们往往只是作为前期的笔试题,栈经常出的题目就是给出一个栈的入栈序列,问下面哪个不可能是这个栈的出栈序列。栈和队列作为算法题并不多,常见的就是如何用两个栈来实现一个队列或者利用一个辅助栈来将一个栈中的元素排序
[我的面试经历:有道一面遇到利用一个辅助栈来将一个栈中的元素排序]
一般来说,Android开发岗位的算法面试是不会出题要求面试者临时设计一个数据结构来解决某个问题,大多数时候只是要求面试者能够熟练掌握常见的数据结构及其实现、能够说出这种数据结构的优缺点即可。2015年校招时我遇到的最常问到的题是实现LRU缓存,这算是一道经典的数据结构设计题,此后的面试中再也没怎么见到过其他的数据结构设计题。更多数据结构相关的实现细节请参考阅读数据结构与算法设计专栏
1.2 算法时间复杂度的计算
一般算法面试的时候,面试官在你给出了解法之后都会问下你这个解法的时间复杂度是多少,如果时间复杂度较高他就会要求你想出一个更优的解法,所以平时有必要练习下算法时间复杂度的计算。算法的运行时间主要有三种表示符号,但是最常见的就是大O表示法。此外,算法导论中介绍了三种时间复杂度的计算方法,分别是代换法、递归树法和主定理法。
下表是常见的算法时间复杂度值及其相应的算法问题举例,例如平方阶时间复杂度是一些基于比较的排序算法的时间复杂度,例如选择排序、冒泡排序等。nlgn阶时间复杂度是随机数字序列的最优排序算法的时间复杂度,例如快速排序等。

下表是常见的递推公式对应的算法时间复杂度和算法问题举例,例如合并排序是nlgn阶,握手问题是平方阶,汉诺塔问题是指数阶等。这个建议结合具体的例子记忆一下,以便快速反应。

下表是主定理法在三种情况下的求值公式。主定理通常可以解决类似
T(n) = a T(n/b) + f(n) 这种递归形式的问题,即将规模为n的问题划分为a个子问题,每个子问题的规模是n/b,这里a和b是正常数,划分原问题和合并结果的代价用函数f(n)描述。

1.3 常见的算法思想
(1)Induction(推导)、Recursion(递归)、Reduction(规约)和Divide and Conquer(分治)
这四个思想比较接近,在《Python Algorithms》这本书中都有提到,我放在一起介绍:
-
Induction(推导)是指数学意义上的推导,类似数学归纳法,主要是用来证明某个命题是正确的。首先我们证明对于基础情况(例如在k=1时)是正确的,然后证明该命题递推下去都是正确的(一般假设当k=n-1时是正确的,然后证明当k=n时也是正确的即可)
-
Recursion(递归)经常发生于一个函数调用自身的情况。递归函数说起来简单,但是实现不太容易,我们要确保对于基础情况(不递归的情况)能够正常工作,此外,对于递归情况能够将递归调用的结果组合起来得到一个有效的结果。
=> 不难发现,Induction(推导)和Recursion(递归)其实彼此相互对应,Induction是自下而上的推导(例如从n-1到n),而Recursion是自上而下的递归(例如从n到n-1)。
-
Reduction(规约)是指问题转换,将一个未知的问题转换成我们能够解决的问题。
-
Divide and Conquer(分治)指将原问题划分成几个小问题,然后递归地解决这些小问题,最后综合它们的解得到问题的解。
=> 仔细分析可知,Induction(推导)、Recursion(递归)和Divide and Conquer(分治)其实都是某种形式上的Reduction(规约),也就是说它们的本质都是对问题进行规约!
这四个概念有一个共同特点:它们都专注于求出目标解的某一步,我们只需要仔细思考这一步,剩下的就能够自动完成了。有点晕?_? 好吧,其实你可能已经对上面几个概念很熟悉了,只是平时没有这么去想过,下面我们举最常见的排序问题为例来阐述下其中的算法思想。
我们如何对排序问题进行Reduction呢?很显然,有很多种方式:
-
假如我们将原问题reduce成两个规模为原来一半的子问题,然后合并子问题的解,这是我们最为常见的二分分治策略,这样我们就得到了合并排序;
-
假如我们每次只是reduce一个元素,并假设前n-1个元素都排好序了,那么我们只需要将第n个元素插入到前面的序列即可,这样我们就得到了插入排序;
-
假如我们每次还是reduce一个元素,这次我们找到其中最大的元素然后将它让在最后一个还没有放置元素的位置上,一直这么下去我们就得到了选择排序;
-
假如我们每次还是reduce一个元素,这次我们找到第k大的元素,然后将它放在位置k上,一直这么下去我们就得到了快速排序。
怎么样?我们学过的排序算法经过这么reduce基本上都很清晰了,不是吗?
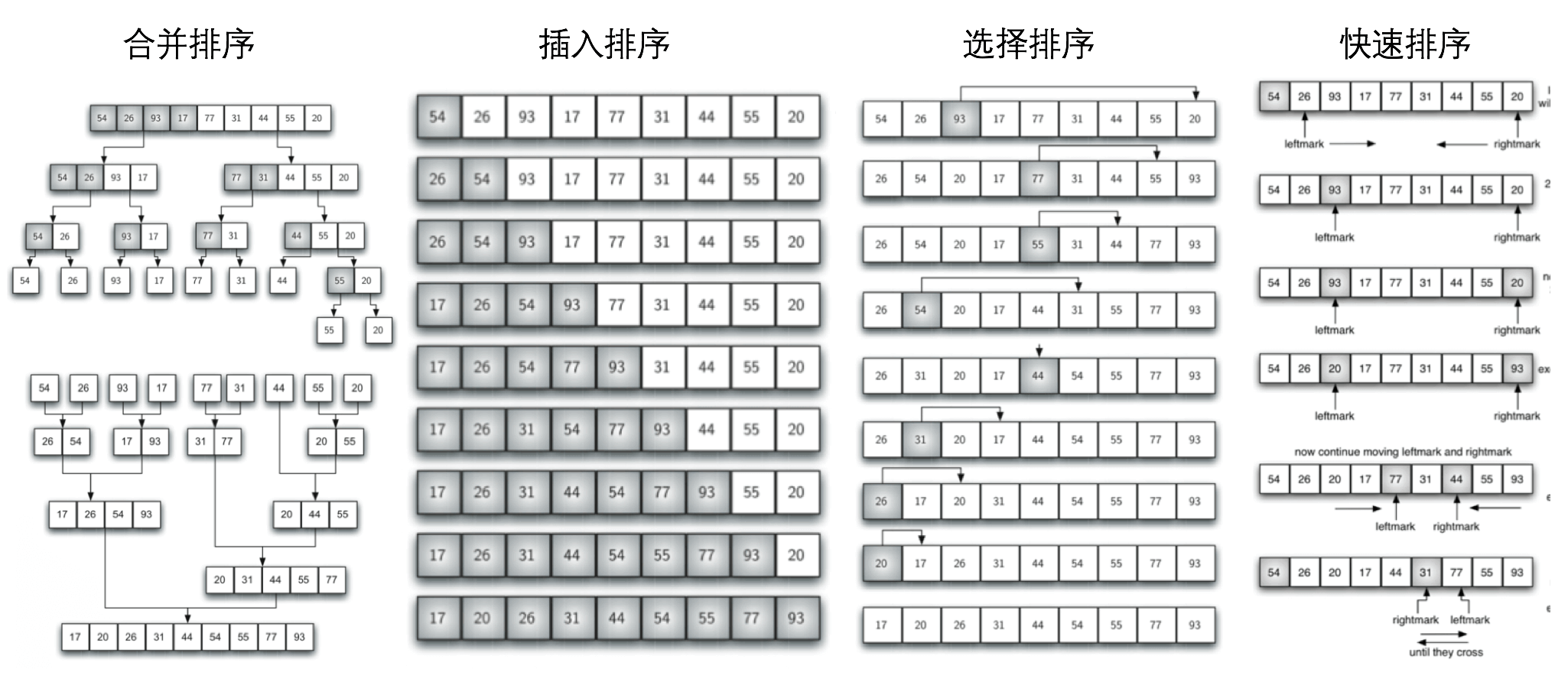
为了能够对问题使用Induction或者说Recursion,Reduction一般是将一个问题变成另一个或者几个只是规模减小了的相同问题。那么,这样做就万事大吉了吗?
其实并不是的,有些时候我们可能还需要考虑Reduction或者说分治策略的子问题平衡性。对于同一个问题,分治时采用 T(n)=T(n-1)+T(1)+n 和 T(n)=2T(n/2)+n 两种解决方案的时间复杂度是不同的,这里就不展开说了,这四个算法核心思想的更多细节请参考阅读数据结构与算法设计专栏