title: "二叉树"
date: 2015-06-25 08:59:24
categories: 数据结构
tags: 数据结构
概念
- 树的最大度为2;
-
分左右子树;
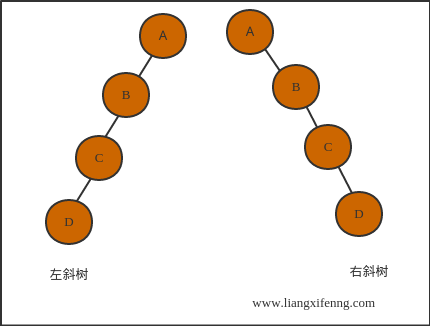
斜树
- 左斜树:所有结点都只有左子树的二叉树;
- 右斜树:所有结点都只有右子树的二叉树;
- 其实在业务罗辑中如果真有这样的需求,那直接使用
线性表就可以了;
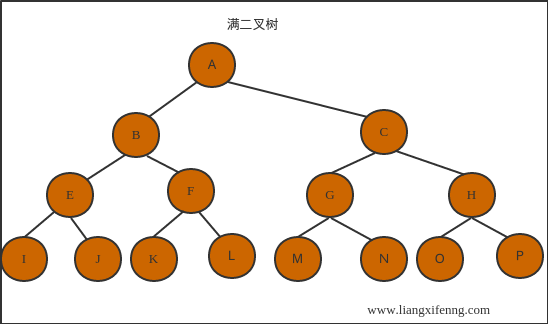
满二叉树
- 所有分支结点的度为2;
- 所有叶子结点只能分布在最下层上;
-
同样深度的二叉树中,满二叉树的结点数最多,叶子结点数最多;
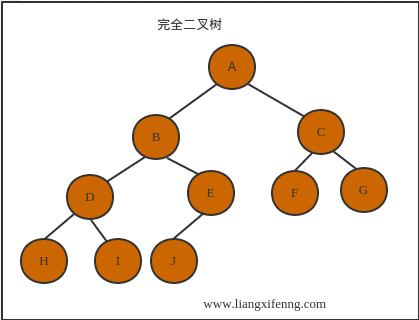
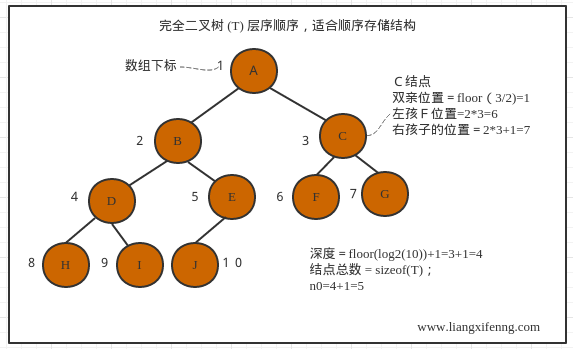
完全二叉树
- 二叉树从根结点出发,按着层次从左到右遍历,第i个结点的位置与满二叉树中对应结点位置完全相同;
- 所有叶子结点只能出现在最下两层;
- 若结点度为1,则该结点只有左子树,不存在只有右子树的情况;
- 结点分配
先左后右;
规则(特性)
- 每层结点数:二叉树的第i层上最多有 (n=2^
i-1)个结点,(i>=1);
- 所有结点数:深度为K的二叉树最多有(n=2^
K-1)个结点,(K>=1) ; - 对于任意一棵二叉树,n0 =叶子结点总数、n1=度为1的结点总数、n2=度为2的结点总数、n=总结点数:n0=n2+1
- 分支线总数=n-1=n1+2n2;
- n=n0+n1+n2;
- n0+n1+n2-1 = n1+2n2 =>
n0=n2+1;
- 满二叉树的深度:log2(n+1);
- 完全二叉树的深度:向下取整数(log2n)+1;
- 因为完全二叉树的所有叶子结点只能出现在最下两层,并且倒数第二层是满的情况,所以倒数第二层所在深度+1也是完全二叉树的深度;
- 层序遍历二叉树的顺序,对于任意一个结点编号 i(1<=i<=n),i可以理解为数组下标+1,因为数组下标是从0开始的:
- 双亲结点编号:向下取整(i/2);
- 如果2i>n,则该结点无左孩子,否则左孩子结点是 2i;
-
如果2i+1>n,则该结点无右孩子,否则右孩子结点是2i+1;
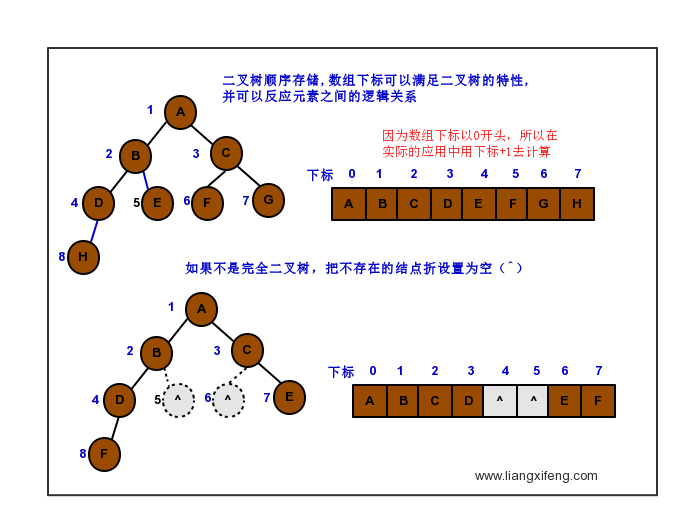
存储方式
-
顺序存储,方便查询操作,并且可以根据层序遍历,合理的利用以上特性;
binary-tree-arr - 链式存储,方便新增,删除操作;结构为数据域+左孩子指针+右孩子指针 (二叉链表),如果有必要的情况下可以添加双亲指针,指向结点的双亲(三叉链表),这都是根据业务需求
灵活控制的;
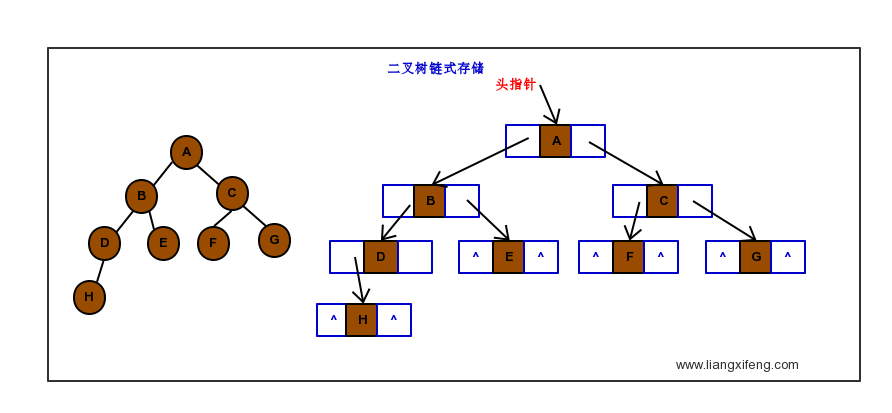
binary-tree-arr
总结:正是因为完全二叉树有以上这些规则和特点,所以我们在日常使用中尽量使用完全二叉树,存储方式最好选择顺序存储;
二叉树的遍历
- 主要针对链式存储,按着一定顺序访问各个结点,保证每个结点仅被访问
一次,以下是根据结点访问顺序定义的;- 前序:先
访问根结点 -> 遍历左子树 -> 遍历右子树;先访问根结点
- 中序:遍历左子树 ->
访问根结点 -> 遍历右子树;中间访问根结点 - 后序:遍历左子树 -> 遍历右子树 -> 后访问根结点;
后访问根结点 -
层序:自上而下,从左到右逐层访问结点;
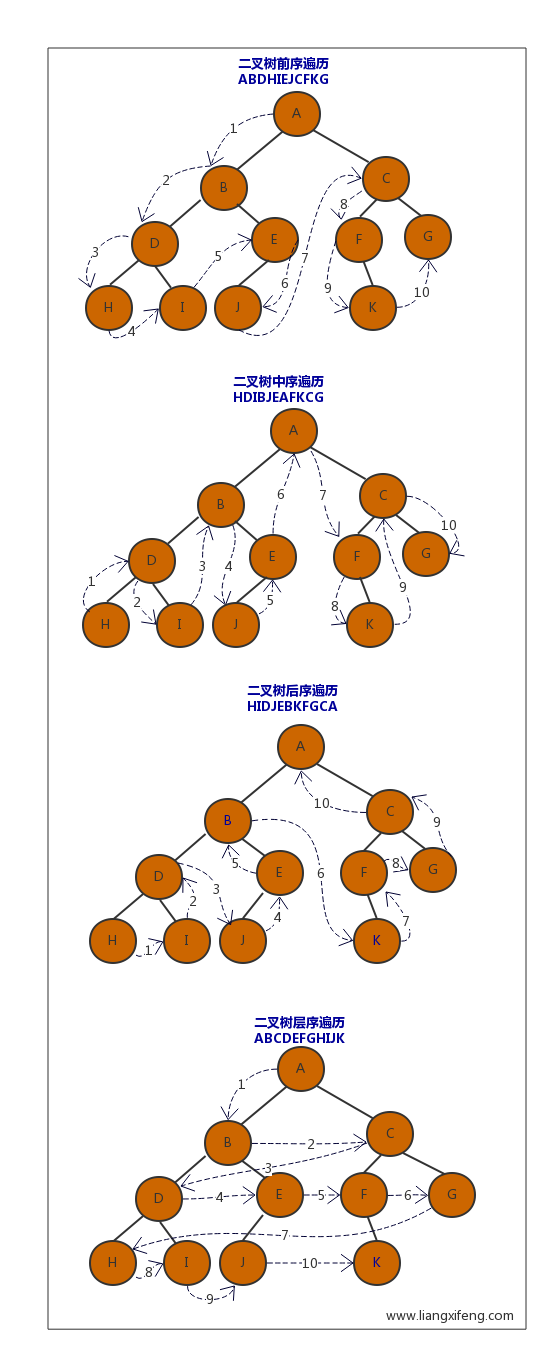
- 前序:先
推导
- 已知前序、中序,可以唯一确定一个二叉树;
- 已知后序、中序,可以唯一确定一个二叉树;
- 但是已知前序、后序却不能确定一棵二叉树;
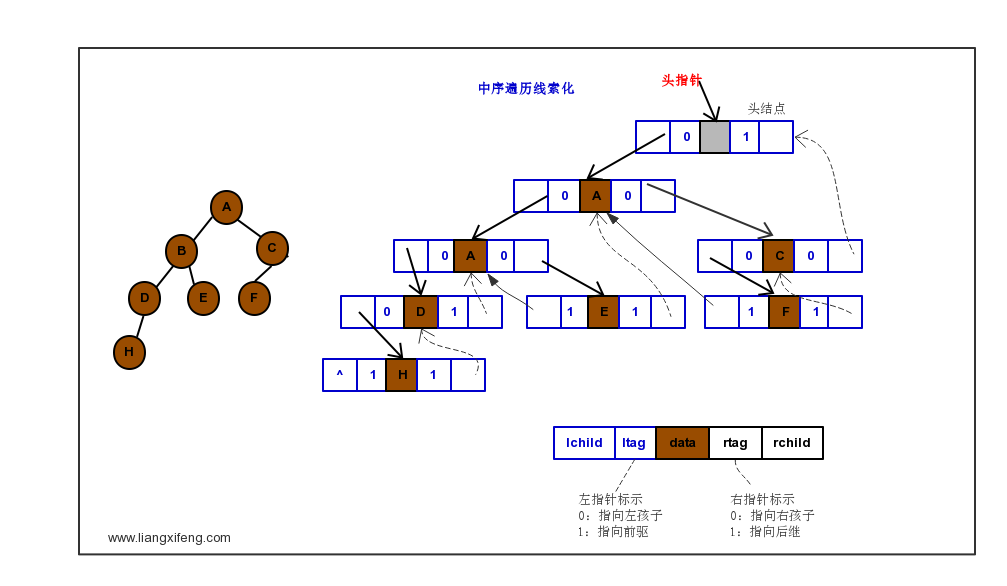
线索二叉树
- 结点度<1的情况,相应的空指针域遍历时候指向它的前驱或后继;
- 一次遍历可以多次使用,在以后的应用中减少遍历算法,可以直接使用第一次遍历的结果;
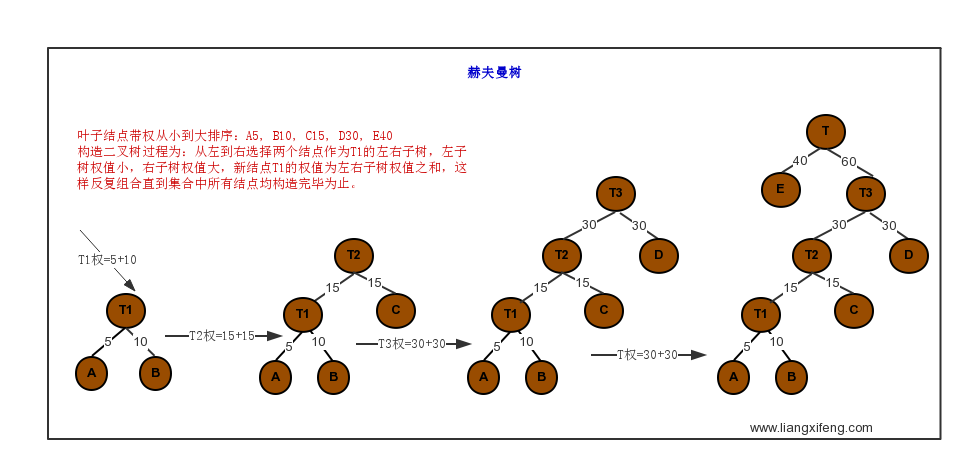
赫夫曼树
- 路径:结点之间的分支构成两个结点之间的路径;
- 路径长度:两个结点之间的分支数量;
- 树的路径长度:从树根到每一结点的路径长度之和;
- 叶子结点带权路径长度:叶子结点到根结点的路径长度*叶子结点权值;
- 树的带权路径长度 WPL: 所有叶子结点带权路径长度之和;
-
赫夫曼树: WPL 最小的二叉树。也称最优二叉树;
WPL
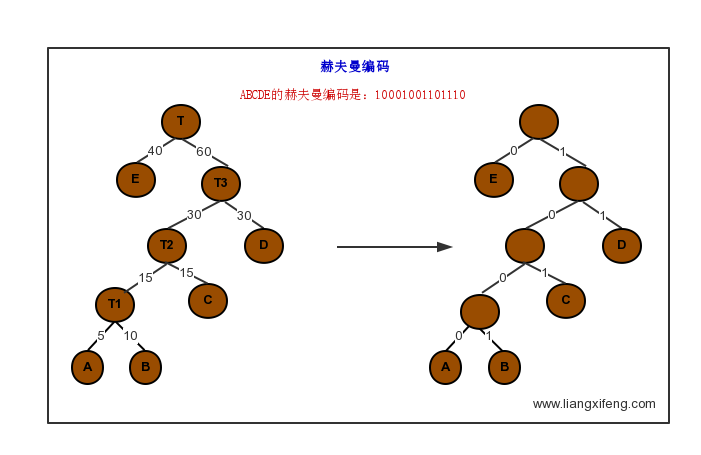
赫夫曼编码
- 赫夫曼树左分支代表0,右分支代表1
- 从根结点到叶子结点经过的分支组成0和1的序列称为叶子结点对应的字符编码,即
赫夫曼编码。
WPL-code