Cardano（ADA）的共识算法Ouroboros

一、前言

2018年的公链将会毫不意外的统一转向pos共识方向，pow将会被扫入历史中。

在我认为，pos代表的就是不再需要从现实中将价值输入至区块链体系(pow消耗现实中的算力达成区块链的价值体系)，而是根据已有的“历史”来不断衍生出新的价值来维护区块链的价值体系。也就是说，所谓权益证明(pos)就是能根据历史所产生的“权益”，使用一套算法能利用好历史中的“权益”来达成共识从而不断衍生出的新的价值，使得区块链本身就能成为一个闭环(而不像pow一样从外界，也就是算力来输入)，不断运行下去。

在区块链算法原理之：Casper 和Tendermint共识算法的比较这篇文章中提到：

有很多不同的方式来实现权益证明的算法，但是权益证明设计的两个主要原理是基于链的PoS和基于拜占庭容错(BFT)的PoS。

Ada的共识算法 Ouroboros（乌洛波洛斯，也就是衔尾蛇）由于其严谨的学术性和在顶级密码学刊物上发表的论文而闻名，并且是 “Ouroboros是第一个被工业界采用的学术界提出来的可证明是安全和健壮的POS算法。(引用自maxdeath菊苣的回答)” (虽然我不确定和dfinity的那边相比谁才是第一)

本文即将根据 Ouroboros 的论文 “Ouroboros: A Provably Secure Proof-of-Stake Blockchain Protocol”及IOHK在youtube上的视频解说：Bernardo David, IOHK Research, Proof-of-Stake Protocol 对Ouroboros的运作流程进行自己浅薄的解释。

若有错误，欢迎大家指出。

本文首发于我自己的知乎专栏金狗喵喵喵的区块链研习

如需转载，需取得同意并标明出处！

毫无疑问，Ouroboros是 “基于链的PoS”。

首先先要声明：论文中的Ouroboros是一个理论，说的是按照什么样的一个流程可以设计出一个健壮的pos算法并给出充分的证明，而Cardano中的Ouroboros是对论文的实现，在实现上和论文中的描述有所不同。

我并没有看过 Cardano 的实现，所以主要是根据论文并结合Cardano来讲Ouroboros是怎么设计的

maxdeath菊苣在很多回答中都指出了：下文引用

本质上，POW和POS都是一种随机选择下一个区块上传者的方式。

所以Ouroboros的根本目的就是为了根据权益多少，随机的选出一个记账者，并且随机选择的这个过程是不可预知的。

二、Ouroboros 总体运行流程

开头先简单描述一下Ouroboros运行的流程：

首先是一些术语及作用的解释：

在Cardano的运行中，时间被分为 slot
每个slot只能产生一个块，若这个块有问题，或者应该产出这个块的“矿工”(也就是stakeholder的候选人)不在线，或者产出的块没有广播给大多数人，那么这个slot是当作废弃的，也就是会跳过这个slot的块。
多个slot为一个 epoch，权益的计算是以每个epoch开始前的历史来计算，也就是说在这个epoch中所产生的权益变化不影响当前的这个epoch中的slot的出块者的选择和其他和历史相关的东西。当前epoch中所产生的这些历史只能在以后的epoch中生效。
每个epoch的开头有个 genesis block(注意是每一个epoch，不是整个链)，这个genesis block 不会上链(整个链初始的那个genesis会，当然这一点可以根据实现自己决定)，而是当前这个节点(矿工)自己在内存中生成，这个genesis block会记录好当前这个epoch中的可能参与出块的 stakeholder的候选人，及一个随机种子ρ。
stakeholder是权益持有者，也就是潜在矿工，在Cardano的实现中权益stake并不是直接指代有多少Ada，而是和有多少Ada相关联(更详细的我不是很清楚)，同时要成为一个stakeholder需要有2%的Ada才行。当然论文中不关注这些，直接定义了stakeholder。而stakeholder并不一定要参与出块，只有记录在每个epoch的genesis block中的stakeholder才能参与当前epoch中slot的出块，所以记录在每个epoch中的genesis block中的stakeholder叫做 “stakeholder候选人”
由这些epoch衔接而成的链就是由Ouroboros共识产生的链，这个链的基本属性和Bitcoin相同(如每个块包含上一个块的hash等等)。
Slot Leader Selection 是指根据权益占比选择按概率选择出当前slot的出块者。指代的是在当前的epoch中，按genesis block 中记录的stakeholder候选人的权益分别占用的比例为这个epoch中的每一个slot选择出块者的概率(注意这个概率是独立事件，也就是有可能在同一个epoch中重复选出相同的人)。在论文中用函数
$\mathbf{F}(\mathbb{S},ρ,sl_{j}) \; \; outputs \; \; U_{i}\in {U_{1},...,U_{n}}\\ 其中\mathbb{S}表示stakeholder候选人集合,ρ表示随机种子,sl_{j}表示第j个slot,U表示出块者(slotleader)$
来表示按照权益占比为概率从stakeholder候选人选出该slot的出块者U。注意在论文中只是定义了这个函数具有这样的作用，在Cardano中使用了 “follow-the-satoshi(fts)” 算法(fts具有论文中定义的这个函数的性质)来选出这个slot leader也就是出块者。
secure multiparty computation (MPC) MPC协议，参与者使用一种能达成MPC的密码学协议来参与生成下一轮epoch的随机种子ρ，这个MPC协议必须是保证guarantee output delivery(G.O.D，下文会解释)。这个随机种子ρ是用于Slot Leader Selection中的。

在已有这些基础术语及作用的基础上，现在来简单介绍一下的工作流程:

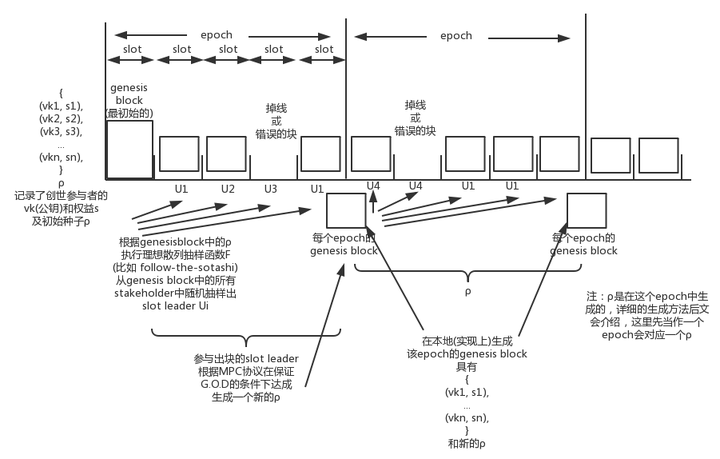
如图所示，执行流程如下：(注：我并不保证这个流程是完全符合Cardano源码的实现(毕竟我没看过)，但是是符合论文的描述的)

从链的真正创世块开始，硬编码进入了一些公钥和这些公钥vk对应的权益s及初始的种子ρ，之后，这个epoch会采用这些基础信息继续运行。
每个节点自己独立运行代码，根据当前epoch的种子ρ，执行F(比如 follow-the-satoshi)，把genesisblock中的权益，ρ和slot的index作为输入，根据概率获得当前这个slot应该由谁出块。

若发现是自己出块，则执行打包交易等等操作，和bitcoin没有太大区别，但是除了基础工作之外，还会生成一个随机数，但是这个随机数不放到链(块)中，而是放一个承诺(后文解释)。
若不是自己出块，则等待出块者出块并广播。收到这个块的时候就进行和bitcoin类似的检查，要是长时间未收到(超出这个slot的时间)则会认为这个slot的块废弃。

在当前epoch中不断重复2的流程直到这个epoch中的所有slot结束。
在整个epoch的过程中会产出一个在这个epoch参与出块者们(slot leaders)都共同认同的随机种子ρ。
在自己的内存里记录好这个ρ及下一个epoch参与的stakeholders，开启下一个epoch周期，进入2的流程。

以上就是 Ouroboros 大致执行的流程。

三、详细解析

根据上一章所描述的Ouroboros的模型及结合目的“产生一个不可预测的随机数”，我们来探讨一下其中的关键问题：如何随机的选出记账者

我们可以发现，在Ouroboros中，由于epoch的模型，这个问题被拆分成两个部分：

产生一个随机种子ρ
根据随机种子ρ在当前epoch中以权益的比例为概率，随机选出slotleader

以每一个epoch为分析单位，那么只要每一个epoch的执行流程是成立的，那么不断重复epoch生成的链就是成立的。(就像该算法的命名Ouroboros，衔尾蛇一样)

那么我们就来分别解释着两个问题

1. 产生一个随机种子ρ

产生这个随机种子的方法在密码学中应该属于交互式协议

首先需要介绍一些东西：

coin tossing (投硬币)

coin tossing 是为了在多方通信中，通过伪随机数和互相交互，最终得到一个统一的，被所有人认可的真随机数的交互式协议。如下图的左边所示：

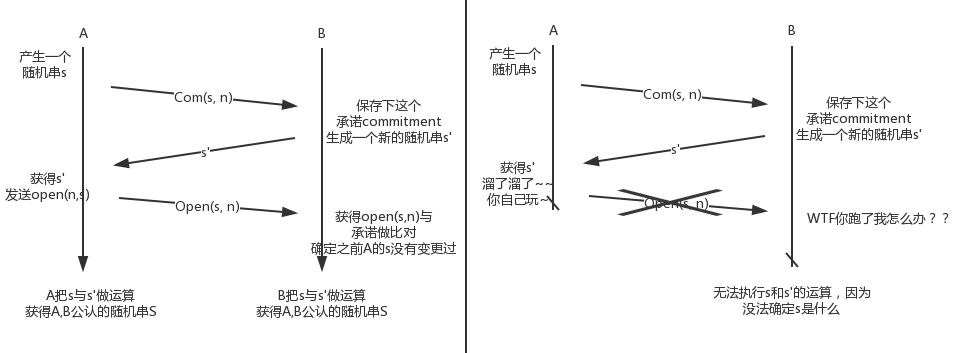
左图是一个2方进行coin tossing 的过程：

A首先产生一个随机串s和一个nonce，然后用A和B都认可的加密方式进行加密
此时加密的结果称为一个承诺(Commitments)，A把这个承诺发送给B，此时相当于B知道A已经产生了一个东西，虽然不知那是什么，但是它已经存在了
B保存这个承诺，然后自己生成一个自己的随机字串s'，并发送给A
此时A同时具有了A自己的字串s和B的随机字串s'，那么A就发送一个揭露(或者打开Open)给B，包含自己一开始的s和nonce
B收到open后使用open的数据加密，把结果和之前的承诺做对比，发现一致，那么B就可以肯定A发送的open就是在发送B自己的随机串之前就确实生成好并存在的。
此时A和B都分别拿到了对方的随机串，并能肯定对方生成自己的串的时候是不知道自己的随机串的信息的，所以即便两方都是使用伪随机生成的字符串，那么对这两个字符串做一些统一的操作(比如异或xor)之后的结果一定是一个真随机字串S，并且被双方所认可。

当把这个两方的coin tossing 扩展为多方的时候，就是一个多方coin tossing的交互式随机数生成协议了。

但是呢，我们可以看到，这种交互至少需要3步(左图描述的过程)，我们可以发现，要达成这样的交互式协议是不能比3步更少的(可以更多，比如一般google到的coin tossing会是4步，例如B并没有直接给s'，而是给了一个Com(s',n')，然后需要第4步B发送给A一个Open)。如果少于了3步，就会出现右图的情况，协议出现了Abort!

在右图的执行流程中：

A首先产生一个随机串s和一个nonce，然后用A和B都认可的加密方式进行加密
B给了A自己的s'，此时A和B完成基本的信息交互
但是此时A自己跑了(不管是作恶还是自己挂了，还是网络断开没法发送了)，那么此时A没有把自己的Open发送给了B，此时会导致整个协议无法执行下去，因为现在A具有了所有的信息，但是B没法具有所有的信息，所以没法达成被双方都认可的随机字串

虽然最终这样并不是作恶成为A可以控制最终字符串的产生，但是A这样的行为却可能导致最终的协议无法执行下去，进而被中断(Abort)。而且即便是多步也会有Abort的行为发生使得协议无法执行下去，而太多的通信则会造成整个网络的拥堵(特别是多方的情况下，有k次通信就是O(n^k)的通信复杂度)。

所以如果能在尽可能少的通信下(如三步)又希望保证整个协议不会因为Abort而无法运作下去，这样的目的就被称为guarantee output delivery(G.O.D)

那么为了保证G.O.D这个目标成立，就需要引入一些新的机制，如下文所述。

verifiable secret sharing (VSS)

verifiable secret sharing (VSS) ：可验证的密钥分享。在Cardano中使用的是PVSS，见链接乌洛波罗斯协议论文与实现的区别。

这里先介绍VSS:

把一个秘密S 通过 share(s) 可以拆分成 m 份，分发给m个人，每个人拿到其中的一片并不知道整个S 是什么但是只要收集到另外t(t<m)个人的秘密(总共具有 t+1 份) ，就可以重新恢复reconstract(si,...,st+1) = S 出这个秘密

因为我并不是学密码学的，所以就不班门弄斧了，下文只能简单介绍一下VSS能起到的作用。

在视频里面举的例子如下：

S               share(S) -> S1, S2, ...  // 比如我原本有一个秘密S，通过 share(S) 把密码拆成了4份
share(S) = Sa, Sb, Sc, Sd
Sa  Sb  Sc  Sd   // 把这4份秘密分别给4个人
A   B   C   D
// 比如按照如下的方式赋值分解出的各个秘密，xor是异或，
// 可以看出A,B,C,D分别拿到的秘密 Sa, Sb, Sc, Sd 都是不可能知道原来的S是什么的
Sa = S xor Ra    R is random str
Sb = S xor Rb
Sc = S xor Rc
Sd = Ra xor Rb xor Rc
// 但是只要其中有人能收集到别人的秘密，比如A自己向B,C,D收集到了另外3个秘密
// 那么 A 就可以把这些秘密全部执行 xor, 由于xor 的性质，就能恢复出原本的 S
reconstract(Sa, Sb, Sc, Sd) = Sa xor Sb xor Sc xor Sd=S

以上只是从原理上简单描述VSS能够做到的事情。我们可以发现，VSS的特点就在于，每个人拿到的那个秘密是不能可能知道原来的秘密是什么的，必须得到他人的“帮助”才能恢复出原来的秘密是什么。

而VSS得特点在于，每个人并不是要拿到所有的密码，而是拿到一定多的秘密(剩余的秘密可以为空，可以为假等等)就可以重新恢复出原来的那个秘密S。

这个特性可以达成一个功能：例如A向大家宣告我有一个东西，然后A就可以用VSS把这个东西分发给所有人，但是所有人又不知道这个东西是什么。此时，即使A挂了或者跑路了，大家也可以互相通信恢复出A一开始的东西。

那这个VSS有什么用途呢？先回到coin tossing 的最后一个问题，协议要是中断了怎么办？

显然，VSS就是用来解决coin tossing 协议中断执行的问题

G.O.D coin tossing

coin tossing 的问题在于要是 A 没有发送open给B，那么协议就无法执行下去。那么联系起VSS的性质，我们就可以很自然的得出：要是open会因为意外原因导致协议中断，那么我们把open分发给所有人不久可以了么？因为即使A跑路了，大家也可以互相通信恢复出A一开始给出的承诺是什么东西，使得coin tossing的协议能够正常执行下去，得到大家都认可的真随机字串。

所以把 VSS 和 coin tossing 结合起来的时候，就可以达成 G.O.D 的目标，称为 “G.O.D coin tossing”

所以在论文中提出的方案如下：

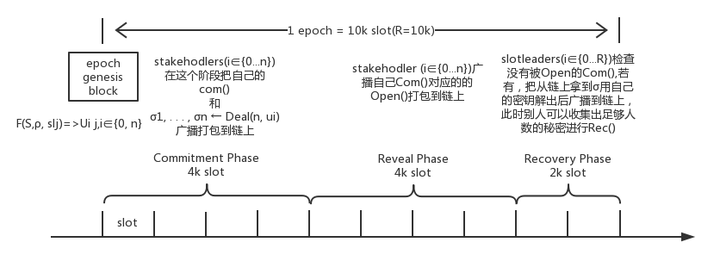
如图所示：

注：这里的Deal()对应上一章节中的Share() 并对share的结果使用对应接受者的公钥进行加密

Ouroboros采用的方法如下：

把每个epoch的slot分成10等份，这里的k是倍数，在Cardano中可以通过配置文件指定
整个epoch被分为了三个阶段：Commitment Phase, Revel Phase, Recovery Phase，分别占比4:4:2

(注：我之前的文章有点错误，现在重新更正如下：)

那么G.O.D coin tossing 的执行流程如下：

首先先注意，在epoch genesis block生成的时候(也就是ρ产生的时候)，实际上每一个slot的slotleader已经被选出来了(划重点)，也就是说在epoch开始的时候就已经知道整个epoch中分别是谁出块了，只是选出的方式是按权益概率决定的(下一章节会详细解释)。另一方面genesisblock中包含的是S=>{(vk1,s1),(vk2,s2),...,(vkn,sn)}也就是不止权益，还有stakeholder候选人的公钥

在Commitment阶段的时候，也就是在整个epoch的前4/10的时间内，所有的stakeholders(i∈{0...n})必须把自己的随机字串生成做处理后并把这个内容广播出去被前4k的leader打包进入区块。(当然如果这个时间内没有把自己的随机字串广播出去的话就相当于放弃了参与下一个epoch随机的权力了)而这个处理的内容是2部分：

这个随机字符串的承诺Commitment
把Open的内容做VSS后对应所有的leader，使用这些leader的公钥(在genesisblock中有)进行加密，也就是Deal的过程，生成σ1, . . . , σn 被加密过的shared secret

在Reveal阶段中，是epoch的中间4/10时间内，这些stakeholders(i∈{0...n})把自己的Open广播出去。此时就会出现有人跑路了，有人掉线，网络不好等等情况这个人的Open没有被打包到链中，此时若没有下一个阶段救场的话就相当于cointossing协议被Abort了。若所有的Open都在的话，那当然就已经可以得出下一个epoch的ρ是什么了
在Recovery阶段的时候，也就是epoch最后2/10的时间内，这些诚实的slotleaders (i∈{0...R})就会检查出有哪些Open没有成功，那么他们就会把没有成功Open对应的秘密自己解密后(前面被公钥加密过)，广播出去上链条，那么这样每个人都可以收集到足够数量的共享秘密而恢复出没有被Open的随机字符串，G.O.D满足。此时所有人都获得了所有人的随机字符串，那么就可以得出一个统一的随机数ρ了。

至此，如何在一个epoch中生成一个不可控制的随机数ρ就解释完成了。我们可以看出通过G.O.D coin tossing 是可以做到一个不会被Abort的交互式随机数生成过程。

下面是论文原文中的算法，注意用红框框出来的地方：

请注意在前两个阶段指的是所有的 stakeholders(i∈{0...n})，是所有的stakeholder都参与，然后Recovery阶段只有被选中的stakeholders才参与。这块地方我之前的理解有误，认为是所有阶段都是只有被选中的stakeholders才参与(slotleaders)。这里特地更正。

(但是还是有点奇怪，更细节的部分我之后会看了源码后再更正的。。。)

根据Cardano结算层的文档来看，在实现上是和论文有区别的。

Slot leaders are elected from the group of all stakeholders. Please note that not all stakeholders participate in this election, but only ones who have enough stake (for example, 2% of the total stake). This group of stakeholders are known as “electors”.

具有权益的确是就是stakeholders，但是注意参与过程的人并不是所有的stakeholders，而是只有2%以上的人才能参与，而这些2%以上的人就叫做“electors”。

而后续的那些操作都是基于electors的。(并不是所有的stakeHolders了)

2. 根据随机种子ρ在当前epoch中以权益的比例为概率，随机选出slotleader

在论文中这部分没有详细描述，只是直接定义出了这样一个函数。那么在Cardano中的实现使用的是“follow-the-satoshi”算法，见链接：术语表

follow-the-satoshi算法最原始是来自于论文：Proof of Activity: Extending Bitcoin’s Proof of Work via Proof of Stake

论文大致是说，使用pow产生一堆stakeholders，然后在这堆stakeholders中使用follow-the-satoshi找出出块者，当然Ouroboros对其的改进就是把pow做成了G.O.D coin tossing

follow-the-satoshi的算法其实很简单，在github上有人对其作了一个模拟实现：Realiserad/fts-tree

这里引用README.md中的话：

The idea is simple: The edges the Merkle tree are labelled with the amount of coins in the left and right subtree respectively. Given a psuedo-random number generator, one can randomly select a stakeholder from the tree, weighted by the amount of coins they own, by traversing the tree down to a leaf node, containing one of the stakeholders. Each stakeholder controls a number of coins and a private key used to sign blocks.

并且引用之中的图做个简单的解释：

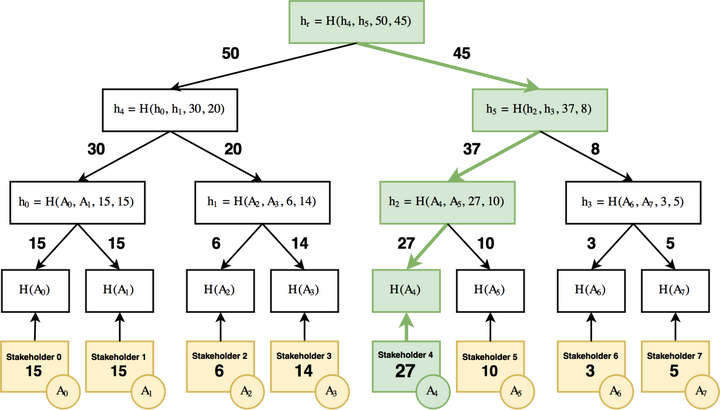
大意就是说，把所有的stakeholder组成一个merkletree的形式，然后根据一个随机种子开始，通过伪随机数做出选择，最终会按照大家权益的比例选出对应的stakeholder。

注意这里强调的是伪随机数，是为了当有一个相同的种子后，每个不同的个体分别执行这个伪随机后都能得到相同的序列。

比如图中的例子，假设我已使用一个种子，每次执行伪随机后可以获得序列{65, 20,15}

这颗树的组成是把stakeholders排列好，按merkletree组织好，附加上每一条边代表两个叶子权益之和。那么我们根据序列从树根开始查找开始：

随机数是65，左边权益是50，那么65>50所以选择右边
执行伪随机得到20，左边权益37，20<37，选择左边
执行伪随机得到15，左边权益27，15<27，选择左边，所以最终选择出A4作为这一轮的stakeholder。

因为比如参与的所有的stakeholder是 A0,A1,...,An，分别对应的权益是s1,s2,...,sn，那么其中Ai, i∈{0,n}的权益比例为：
$\frac{s_{1}}{s_{1}+s_{2}+...+s_{n}}$
那么我是根据随机数进行随机漫步，那么显然最后选中某个stakeholder的概率就是其权益占总体的比例。

又因为是使用一个真随机数作为种子，执行伪随机进行漫步，那么只要所有人拿到的真随机数的种子是一致的时候，那么所有人得到的随机出的stakeholder的结果就是一致的

所以就是可以解释G.O.D coin tossing 中的问题，只要但genesis block 能够生成后得到ρ和权益集合S，那么就相当于直接可以计算出当前这个epoch中所有的slotleaders们都是谁了。

四、总结

本文根据论文和视频描述了Ouroboros整体的执行流程和中间的一些细节。首先先对想出这种思路并给出证明的科学家们致意崇高的敬意，Ouroboros将会开启pos的新篇章。Ouroboros论文最重要的不只是给出这样一种pos的思路，更多的是提出对这个思路的一个论证证明的方式。这种论证的方式可以延续到其他共识算法的证明中。

事实上诚实的说，我并不保证我完全看懂了论文，因为论文中写的实际上很复杂···另一方面，本文也没有解释论文中后半段关于“权益委托”的方式，之后有空慢慢补。

下一篇和pos相关的文章将会描述Dfinity的实现，Dfinity是“基于拜占庭容错(BFT)的PoS”，并在更后面的文章中对这两者做比较。

之后我也会尝试使用c++去针对我司区块链系统实现Ouroboros的共识算法。

本文首发于我自己的知乎专栏金狗喵喵喵的区块链研习

如需转载，需取得同意并标明出处！

eth赞赏地址：0x97d13030451305eFaeC3BD8c8DA963ac032D0750

ada赞赏地址：DdzFFzCqrht7UMeVYfVc4fEGi4ewuwwzkaCHMDTT924UiQCtHidstPU8LVm3sU9giARDKhZqiH2x78LgCs93brYBgvduvWn5zAUDbCmB