二叉树是非常基础又非常重要的数据结构,在一些场合有着非常重要的作用。掌握二叉树对编写高质量代码、减少代码量有很大的帮助!
二叉树是一种特殊的树, 非常适合计算机处理数据, 所以对于程序员来说掌握二叉树是非常有必要的。
二叉树是什么
二叉树是一种特殊的树,有以下两个特征:
- 二叉树的每个结点的度都不大于2;
- 二叉树每个结点的孩子结点次序不能任意颠倒。
为什么使用二叉树
二叉树的前序遍历可以用来显示目录结构等;中序遍历可以实现表达式树,在编译器底层很有用;后序遍历可以用来实现计算目录内的文件及其信息等。二叉树是非常重要的数据结构, 其中二叉树的遍历要使用到栈和队列还有递归等,很多其它数据结构也都是基于二叉树的基础演变而来的。熟练使用二叉树在很多时候可以提升程序的运行效率,减少代码量,使程序更易读。
二叉树不仅是一种数据结构,也是一种编程思想。学好二叉树是程序员进阶的一个必然进程。
二叉树的遍历
二叉树有深度遍历和广度遍历, 深度遍历有前序、 中序和后序三种遍历方法。 广度遍历就是层次遍历。 因为树的定义本身就是递归定义, 因此采用递归的方法实现树的三种遍历容易理解而且代码比较简洁。
有时对一段代码来说, 可读性有时比代码本身的效率要重要的多。
四种遍历的主要思想:
- 前序遍历:访问根–>遍历左子树–>遍历右子树;
- 中序遍历:遍历左子树–>访问根–>遍历右子树;
- 后序遍历:遍历左子树–>遍历右子树–>访问根;
- 广度遍历:按照层次一层层遍历;
例如(a+b*c)-d/e,该表达式用二叉树表示如图:
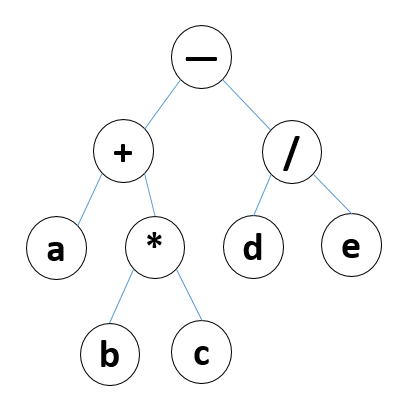
对该二叉树进行深度和广度遍历为:
前序遍历:- + a b c / d e
中序遍历:a + b c - d / e
后序遍历:a b c + d e / -
广度遍历:- + / a d e b c
js中的二叉树
上述二叉树(a+b*c)-d/e在js中可以用对象的形式表示出来:
var tree = {
value: "-",
left: {
value: '+',
left: {
value: 'a',
},
right: {
value: '*',
left: {
value: 'b',
},
right: {
value: 'c',
}
}
},
right: {
value: '/',
left: {
value: 'd',
},
right: {
value: 'e',
}
}
}js中二叉树的深度遍历
先序遍历
递归遍历
var preListRec = []; //定义保存先序遍历结果的数组
var preOrderRec = function(node) {
if (node) { //判断二叉树是否为空
preListRec.push(node.value); //将结点的值存入数组中
preOrderRec(node.left); //递归遍历左子树
preOrderRec(node.right); //递归遍历右子树
}
}
preOrderRec(tree);
console.log(preListRec);
//[ '-', '+', 'a', '*', 'b', 'c', '/', 'd', 'e' ]
先序递归遍历的思路是先遍历根结点,将值存入数组,然后递归遍历:先左结点,将值存入数组,继续向下遍历,然后再回溯遍历右结点,将值存入数组,这样递归循环。
非递归遍历
var preListUnRec = []; //定义保存先序遍历结果的数组
var preOrderUnRecursion = function(node) {
if (node) { //判断二叉树是否为空
var stack = [node]; //将二叉树压入栈
while (stack.length !== 0) { //如果栈不为空,则循环遍历
node = stack.pop(); //从栈中取出一个结点
preListUnRec.push(node.value); //将取出结点的值存入数组中
if (node.right) stack.push(node.right); //如果存在右子树,将右子树压入栈
if (node.left) stack.push(node.left); //如果存在左子树,将左子树压入栈
}
}
}
preOrderUnRecursion(tree);
console.log(preListUnRec);
先序非递归遍历是利用了栈,将根结点放入栈中,然后再取出来,将值放入结果数组,然后如果存在右子树,将右子树压入栈,如果存在左子树,将左子树压入栈,然后循环判断栈是否为空,重复上述步骤。
中序遍历
递归遍历
var inListRec = []; //定义保存中序遍历结果的数组
var inOrderRec = function(node) {
if (node) { //判断二叉树是否为空
inOrderRec(node.left); //递归遍历左子树
inListRec.push(node.value); //将结点的值存入数组中
inOrderRec(node.right); //递归遍历右子树
}
}
inOrderRec(tree);
console.log(inListRec);
//[ 'a', '+', 'b', '*', 'c', '-', 'd', '/', 'e' ]
中序递归遍历的思路是先递归遍历左子树,从最后一个左子树开始存入数组,然后回溯遍历双亲结点,再是右子树,这样递归循环。
非递归遍历
var inListUnRec = []; //定义保存中序遍历结果的数组
var inOrderUnRec = function(node) {
if (node) { //判断二叉树是否为空
var stack = []; //建立一个栈
while (stack.length !== 0 || node) { //如果栈不为空或结点不为空,则循环遍历
if (node) { //如果结点不为空
stack.push(node); //将结点压入栈
node = node.left; //将左子树作为当前结点
} else { //左子树为空,即没有左子树的情况
node = stack.pop(); //将结点取出来
inListUnRec.push(node.value); //将取出结点的值存入数组中
node = node.right; //将右结点作为当前结点
}
}
}
}
inOrderUnRec(tree);
console.log(inListUnRec);
//[ 'a', '+', 'b', '*', 'c', '-', 'd', '/', 'e' ]非递归遍历的思路是将当前结点压入栈,然后将左子树当做当前结点,如果当前结点为空,将双亲结点取出来,将值保存进数组,然后将右子树当做当前结点,进行循环。
后续遍历
递归遍历
var postListRec = []; //定义保存后序遍历结果的数组
var postOrderRec = function(node) {
if (node) { //判断二叉树是否为空
postOrderRec(node.left); //递归遍历左子树
postOrderRec(node.right); //递归遍历右子树
postListRec.push(node.value); //将结点的值存入数组中
}
}
postOrderRec(tree);
console.log(postListRec);
//[ 'a', 'b', 'c', '*', '+', 'd', 'e', '/', '-' ]递归遍历也是和上面的差不多,先走左子树,当左子树没有孩子结点时,将此结点的值放入数组中,然后回溯遍历双亲结点的右结点,递归遍历。
非递归遍历
var postListUnRec = []; //定义保存后序遍历结果的数组
var postOrderUnRec = function(node) {
if (node) { //判断二叉树是否为空
var stack = [node]; //将二叉树压入栈
var tmp = null; //定义缓存变量
while (stack.length !== 0) { //如果栈不为空,则循环遍历
tmp = stack[stack.length - 1]; //将栈顶的值保存在tmp中
if (tmp.left && node !== tmp.left && node !== tmp.right) { //如果存在左子树
stack.push(tmp.left); //将左子树结点压入栈
} else if (tmp.right && node !== tmp.right) { //如果结点存在右子树
stack.push(tmp.right); //将右子树压入栈中
} else {
postListUnRec.push(stack.pop().value);
node = tmp;
}
}
}
}
postOrderUnRec(tree);
console.log(postListUnRec);
//[ 'a', 'b', 'c', '*', '+', 'd', 'e', '/', '-' ]这里使用了一个tmp变量来记录上一次出栈、入栈的结点。思路是先把根结点和左树推入栈,然后取出左树,再推入右树,取出,最后取根结点。
js中二叉树的广度遍历
广度遍历是从二叉树的根结点开始,自上而下逐层遍历;在同一层中,按照从左到右的顺序对结点逐一访问。
实现原理:使用数组模拟队列,首先将根结点归入队列。当队列不为空时,执行循环:取出队列的一个结点,如果该节点有左子树,则将该节点的左子树存入队列;如果该节点有右子树,则将该节点的右子树存入队列。
var breadthList = []; //定义保存广度遍历结果的数组
var breadthTraversal = function(node) {
if (node) { //判断二叉树是否为空
var que = [node]; //将二叉树放入队列
while (que.length !== 0) { //判断队列是否为空
node = que.shift(); //从队列中取出一个结点
breadthList.push(node.value); //将取出结点的值保存到数组
if (node.left) que.push(node.left); //如果存在左子树,将左子树放入队列
if (node.right) que.push(node.right); //如果存在右子树,将右子树放入队列
}
}
}
breadthTraversal(tree);
console.log(breadthList);
//[ '-', '+', '/', 'a', '*', 'd', 'e', 'b', 'c' ]总结
二叉树的遍历还是比较难懂的,如果想要好好的理解,可以把程序转化一下,比如递归的程序可以吧每个递归都写成实际的函数嵌套,这样一层层的直接执行代码,不用递归,就很容易读懂了。