算法
算法(Algorithm)是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。

简单点说,算法就是解决问题的方法。确切来说它是相对于计算机程序的,大多数情况并不与具体某一种编程语言有关,但今天我们采用java语言实现算法示例。原谅我是一只Android小菜鸟,就算不原谅,你又能拿我怎么滴?哈哈,开个玩笑,回到正题,方法有千千万万种,相信大家王者荣耀上分也是想了好多办法,尝试不同的位置,不同英雄,每个英雄不同的打法。最后发现,毫无卵用(手动滑稽)。那是你没找到好的方法,比如你可以找代练啊,而我们的主题算法的优劣主要取决于时间复杂度和空间复杂度。那么有人问了,什么是时间复杂度,什么又是空间复杂度呢?
时间复杂度
时间复杂度是指执行算法所需要的计算工作量。我们见得更多的是这样的写法,O(1)、O(n)。到底什么意思呢?我相信更多的小伙伴想要的是这样的解读方式。
O(1)
int a=1;
int b=2;
int c=a+b;类似于这种,执行语句的频度均为1,即使有上千万条,时间复杂度还是O(1),只不过执行时间是一个很大的常数。
O(n)
for(int i=0;i<n;i++){
int a=1;
int b=2;
int c=a+b;
}在一个规模为n的循环中,不管是n次,还是n-1次,对于时间复杂度都是线性的,取n,记为O(n)。
O(log2n)
int i = 1;
while (i <= n){
i = i*2;
}这个可能理解上有点困难,但也很简单,每次执行i都会乘以2,其实就是2的x次幂小于等于n,求得x为log2n,所以时间复杂度O(log2n)。
O(n^2)
for (i = 0; i < n; ++i){
for (j = 0; j < n; j++){
printf ("%d\n", j);
}
}类似于这种在规模为n的循环中又嵌套了一层规模为n的循环,那么时间复杂度就为O(n^2),同理n的多次幂就是多层嵌套。
空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度。一般来说我们不考虑空间复杂度,大多情况下为O(1),像递归可能会达到O(n)。
排序算法稳定性
稳定性就是一组元素,其中有重复的元素,比如2113,我们把前面的1记为1a,后面的1记为1b,那么原始数据为21a1b3,如果排序后重复元素的相对位置不变,那么,这个排序是稳定的。如上例子,排序完应该是1a1b23才是稳定的,而不是1b1a23。
排序算法
排序算法是算法的入门知识,但思想可以用于很多算法中。什么是排序?排序就是将一组对象按照某种逻辑顺序重新排列的过程。其实在我们的api中提供了很多优秀的排序算法,那我们为什么还要去学习它?原因很简单,它属于入门,有助于你理解其它更高大上的算法,同时它也是我们解决其他问题的第一步。懂了它,你又向大佬靠近了一步。最重要的是面试官看你排序算法这么6,心里想这个肯定是个大佬,一定要留住他,到时候就是你装逼的时候了。

我都懒得说排序算法有几种了,因为我根本不知道,一种排序算法可能对应多种变体,这次我给大家介绍8种常见的经典排序算法。

直接插入排序
思想
直接插入排序很好理解,就是从一组元素中取一个元素(肯定是有序的,就一个嘛,称有序元素组),然后在剩下的元素中每次取一个元素使劲地往有序的元素组插,插到你满意为止。
是不是很好理解?如果觉得还是有点抽象,没有关系,每个算法,我都会分为3个步骤讲解,思想-拆解分析-java代码实现-运行结果。
为了方便起见,排序的原始数据为5201314,很正规,有重复元素,没毛病。这里给大家一个小意见,像碰到/2或者说*2这种,用位运算更佳哦,但本文为了好理解采用了前者,哈哈。
拆解分析
我们在实现直接插入排序的时候往往取第一个元素成立有序元素组,然后它后面的元素一个一个疯狂插。
- 5:取第一个,5
- 2-5:取5后面的2,插入5使之成为有序数组
- 0-2-5:取2后面的0,插入2-5,0比5小,往前走,0又比2小,往前走,没办法,最小了,结束,以下以此类推
- 0-1-2-5:取0后面的1,插入0-2-5
- 0-1-2-3-5:取1后面的3,插入0-1-2-5
- 0-1-1-2-3-5:取3后面的1,插入0-1-2-3-5
- 0-1-1-2-3-4-5:取1后面的4,插入0-1-1-2-3-5
很有层次感是不是?在插的时候也有小技巧的,要温柔,要循循渐进。因为每当我们插入一个元素,都是有序的,有序的说明什么?越后面肯定越大,所以我们只要从后面开始比较就行了(你非要从前面插,我也没办法),我们从后一直往前比较,直到碰到小于或等于插入的元素为止,然后我们乖乖的插到它后面就行了。
java代码实现
public static void insertSort(int[] array) {
//从第2个开始往前插
for (int i = 1, n = array.length; i < n; i++) {
int temp = array[i];//保存第i个值
int j = i - 1;//从有序数组的最后一个开始
for (; j >= 0 && array[j] > temp; j--) {
array[j + 1] = array[j];//从后往前比较,大于temp的值都得后移
}
array[j + 1] = temp;//碰到小于或等于的数停止,由于多减了1,所以加上1后,赋值为插入值temp
}
System.out.println("直接插入排序后:" + Arrays.toString(array));
}从代码的实现来分析,运用我们刚刚学的知识,通常情况下最外层是一个n规模的循环,内部又有一个规模为n的循环,因此平均时间复杂度为O(n^2);最坏的情况是内部的循环全部走一遍,比如我们插入了一个最小的值,因此最差时间复杂度为O(n^2);最好的情况就是里面的循环不用走,比如我们插入了一个最大的值,因此最好时间复杂度为O(n)。其中空间复杂度为O(1)。由于我们是碰到小于或等于的数才停止,所以并不影响重复元素的相对位置,因此直接插入排序是稳定的。
运行结果

希尔排序
希尔排序也是插入排序的一种,是直接插入排序算法的一种更高效的改进版本。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率。
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位。
说了这么多,其实就是插得不够理想,根据直接插入排序的时间复杂度,最好的情况可以达到线性的程度,一般情况下,却不是这样的,每次插入一个,可能要移动大量数据,我们希望在执行直接插入前,能够尽量的保持有序。
思想
取一个增量d1<n,使得距离为d1的元素分在一组,每组进行直接插入排序,然后再取d2<d1,进行排序,直到所有元素都在一组,即增量为1。
拆解分析
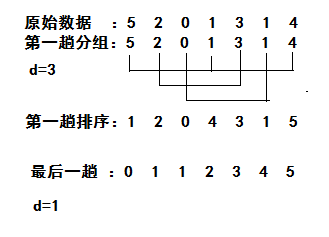
java代码实现
public static void shellSort(int[] array) {
for (int n = array.length, d = n / 2; d > 0; d /= 2) {//取增量为长度的一半,每次减半,直到d=1,但是d=1必须得排序,因此最后的判断为d>0
for (int x = 0; x < d; x++) {//分组
for (int i = x + d; i < n; i += d) {//每组进行直接插入排序
int temp = array[i];
int j = i - d;
for (; j >= 0 && array[j] > temp; j = j - d) {
array[j + d] = array[j];
}
array[j + d] = temp;
}
}
}
System.out.println("希尔排序后:" + Arrays.toString(array));
}希尔排序的最好与最坏时间复杂度同直接插入排序,平均时间复杂度为O(n^1.3),不要问我1.3怎么来的,这跟增量的取值有关系,空间复杂度为O(1),由于在最后一次直接排序前,经过分组排序,所以可能重复元素的相对位置会交换,因此它是不稳定的。
运行结果

简单选择排序
我记得当初老师让我们写一个排序算法,我第一个想的就是这个,可能大多数都是这个?很厉害了是不是?至少也是有名的排序算法。
思想
在一组元素中,暴力找出最小的元素与第一个位置的元素交换,然后从剩下的元素中,选取最小的,与第二个位置交换,以此类推。
拆解分析
- 5-2-0-1-3-1-4,原始数据,遍历所有元素找到最小元素0与第一个位置交换
- 0-2-5-1-3-1-4,然后从剩下的元素2-4中找出最小元素1,这个1是原始数据的第一个1,因为遍历取最小的时候,只有比当前小的才被记录为最小值,最后1与第二个位置元素交换
- 0-1-5-2-3-1-4,从5-4中找出1,与第三个位置元素交换
- 0-1-1-2-3-5-4,从2-4中找出2,与第四个位置元素交换
- 0-1-1-2-3-5-4,从3-4中找出3,与第五个位置元素交换
- 0-1-1-2-3-5-4,从5-4中找出4,与第六个位置元素交换
- 0-1-1-2-3-4-5,最后一个5与最后一个位置元素交换,排序结束
java代码实现
public static void selectSort(int[] array) {
for (int i = 0, n = array.length; i < n; i++) {
int j = i + 1;
int temp = array[i];
int position = i;
for (; j < n; j++) {
if (array[j] < temp) {
temp = array[j];
position = j;
}
}
array[position] = array[i];
array[i] = temp;
}
System.out.println("简单选择排序后:" + Arrays.toString(array));
}从代码上看,简单选择排序似乎没有什么最好最坏的时候,总是这么暴力,时间复杂度总是为O(n^2),空间复杂度为O(1),由于每次取到最小值后都要与前面位置元素交换,因此破坏了元素的相对位置,所以它是不稳定的。
运行结果

堆排序
说堆排序之前,必须说一下堆的概念:
完全二叉树中任一非叶子结点的关键字均不大于(或不小于)其左右孩子(若存在)结点的关键字。而我们这里取不小于,也称之为大根堆。
思想
利用大根堆的性质,每次把元素组建堆,取出最大值,放入最后,直到最后一位,排序完成。
拆解分析
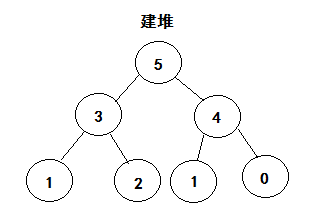
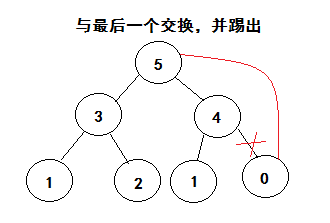
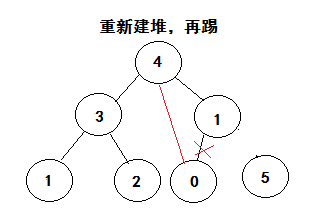
以此类推,直到完成最后一个,排序完成。
java代码实现
public static void heapSort(int[] array) {
//从第一个非叶子结点开始,建堆
int n = array.length;
int startIndex = (n - 1 - 1) / 2;
for (int i = startIndex; i >= 0; i--) {
maxHeapify(array, n, i);
}
//末尾与头交换,交换后调整最大堆
for (int i = n - 1; i > 0; i--) {
int temp = array[0];
array[0] = array[i];
array[i] = temp;
maxHeapify(array, i, 0);
}
System.out.println("堆排序后:" + Arrays.toString(array));
}
/**
* 创建最大堆
*
* @param array 元素组
* @param heapSize 需要创建最大堆的大小,一般在sort的时候用到,因为最大值放在末尾,末尾就不再归入最大堆了
* @param index 当前需要创建最大堆的位置
*/
private static void maxHeapify(int[] array, int heapSize, int index) {
int left = index * 2 + 1;//左子节点
int right = left + 1;//右子节点
int largest = index;
if (left < heapSize && array[index] < array[left]) {
largest = left;
}
if (right < heapSize && array[largest] < array[right]) {
largest = right;
}
//得到最大值后可能需要交换,如果交换了,其子节点可能就不符合堆要求了,需要重新调整
if (largest != index) {
int temp = array[index];
array[index] = array[largest];
array[largest] = temp;
maxHeapify(array, heapSize, largest);
}
}从代码直接看时间复杂度其实挺难,我这里直接给答案,堆排序的平均、最差、最坏时间复杂度都是O(nlog2n),因为它永远都是一个套路,对这个时间复杂度怎么来的,可以网上搜搜,我相信你是棒棒的。空间复杂度为O(1),因为它需要建堆还要重新调整堆,肯定是没法保证元素的相对位置的,所以它是不稳定的。
运行结果

冒泡排序
冒泡排序可以想象一下,鱼吐泡泡,一个一个泡泡往上冒。
思想
元素之间两两比较,最小数往上冒,或者最大数向下沉,直到排序完成。
拆解分析
我们这里以往上冒为例。
- 5-2-0-1-3-1-4,1与4比较,小者1排前面
- 5-2-0-1-3-1-4,3与1比较,小者1排前面
- 5-2-0-1-1-3-4,1与1比较,小者1排前面
- 5-2-0-1-1-3-4,0与1比较,小者0排前面
- 5-2-0-1-1-3-4,2与0比较,小者0排前面
- 5-0-2-1-1-3-4,5与0比较,小者0排前面
- 0-5-2-1-1-3-4,此时完成第0趟冒泡,同理完成剩下的冒泡
java代码实现
public static void bubbleSort(int[] array) {
int n = array.length;
for (int i = 0; i < n - 1; i++) {
for (int j = n - 1 - 1; j >= i; j--) {
if (array[j + 1] < array[j]) {
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
}
}
System.out.println("第" + i + "趟:" + Arrays.toString(array));
}
System.out.println("冒泡排序后:" + Arrays.toString(array));
}如果你单纯从上面的代码看,平均、最好、最差时间复杂度都是O(n^2),如果看过其它文章的同学可能会说最好时间复杂度应该是O(n),那是因为加入了标志位,具体代码我不贴了,空间复杂度是O(1),由于一直是两两比较,并没有改变相对位置的操作,所以是稳定的。
运行结果
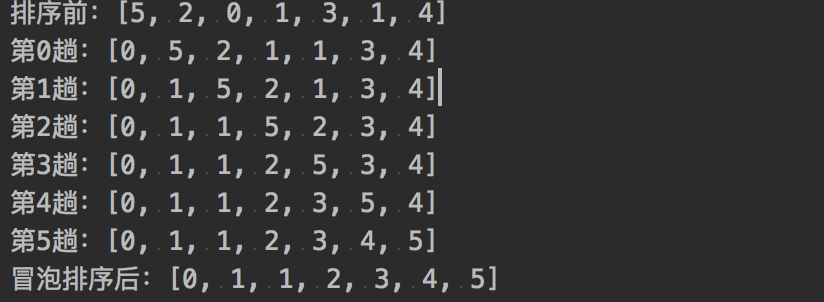
快速排序
思想
选择一个基数,一般我们选择第一个数,然后把大于该数的放右边,小于该数的放左边,然后分别对左右两边用同样的方法处理,直到排序结束。
拆解分析
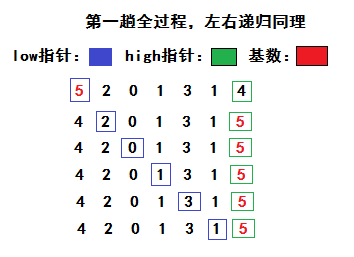
java代码实现
public static void quickSort(int[] array) {
_quickSort(array, 0, array.length - 1);
System.out.println("快速排序后:" + Arrays.toString(array));
}
private static int getMiddle(int[] array, int low, int high) {
int tmp = array[low]; //数组的第一个作为基数
while (low < high) { //直到指针重合一趟完成
while (low < high && array[high] >= tmp) {
high--;
}
array[low] = array[high]; //找到比基数小的
while (low < high && array[low] <= tmp) {
low++;
}
array[high] = array[low]; //找到比基数大的
}
array[low] = tmp; //基数归位
System.out.println(Arrays.toString(array));
return low; //返回基数的位置
}
private static void _quickSort(int[] array, int low, int high) {
if (low < high) {
int middle = getMiddle(array, low, high); //基于第一个数将array数组进行一分为二
_quickSort(array, low, middle - 1); //左边进行递归排序
_quickSort(array, middle + 1, high); //右边进行递归排序
}
}关于快速排序的时间复杂度,表示三言两语真的说不清楚,感兴趣的朋友可以翻阅相关书籍,有能力的可以自己证明- -!最好时间复杂度为O(nlog2n),情况为能够正好根据基数平均划分元素组,最差时间复杂度为O(n^2),情况为元素组呈正序或者逆序状态,平均时间复杂度为O(nlog2n),因为快速排序是递归进行的,需要牵涉到递归深度,空间复杂度为O(nlog2n),准确来说是平均空间复杂度,由于快速排序在跟基数比较的时候,可能会交换而破坏了元素之间的相对位置,因此快速排序是不稳定的。
运行结果
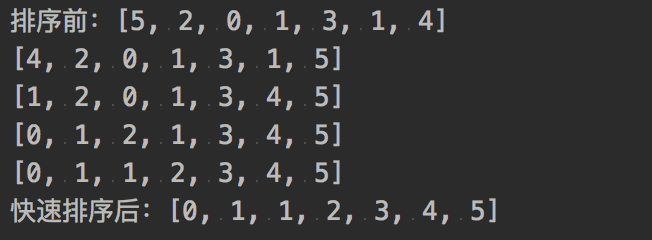
归并排序
思想
采用经典分治思想,将一个元素组划分多个有序的小元素组,然后将这些小元素组合并成一个有序的元素组。
拆解分析
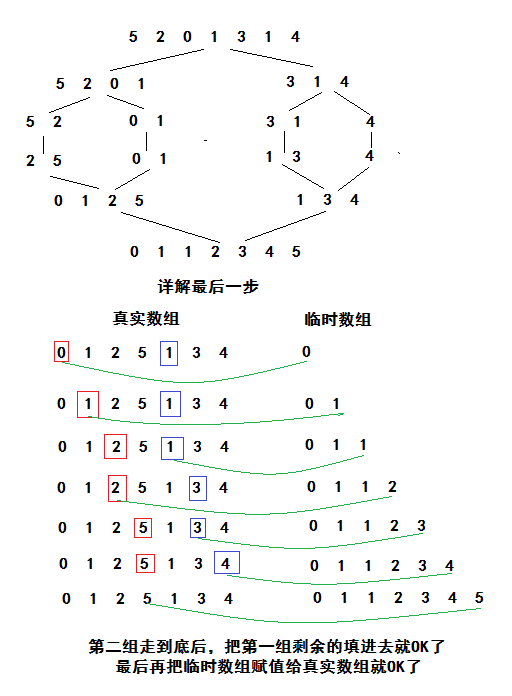
java代码实现
public static void mergeSort(int[] array) {
sort(array, 0, array.length - 1);
System.out.println("归并排序:" + Arrays.toString(array));
}
private static void sort(int[] array, int left, int right) {
if (left < right) {
//找出中间索引
int center = (left + right) / 2;
//对左边数组进行递归
sort(array, left, center);
//对右边数组进行递归
sort(array, center + 1, right);
//合并
merge(array, left, center, right);
}
}
private static void merge(int[] array, int left, int center, int right) {
int[] tmpArr = new int[array.length];
int mid = center + 1;
int third = left;//third记录中间数组的索引
int tmp = left;//复制时用到的索引
while (left <= center && mid <= right) {
//从两个数组中取出最小的放入中间数组
if (array[left] <= array[mid]) {
tmpArr[third++] = array[left++];
} else {
tmpArr[third++] = array[mid++];
}
}
//剩余部分依次放入中间数组
while (mid <= right) {
tmpArr[third++] = array[mid++];
}
while (left <= center) {
tmpArr[third++] = array[left++];
}
//将中间数组中的内容复制回原数组
while (tmp <= right) {
array[tmp] = tmpArr[tmp++];
}
System.out.println(Arrays.toString(array));
}由于归并排序就一个套路而且合并的时候是从左往右,因此不会破坏元素的相对位置,是稳定的,同时它的最好、最坏、平均时间复杂度都是O(nlog2n),简单来说它是基于完全二叉树的,其深度为log2n,每次合并操作都是一个n级规模,因此为nlog2n,而空间复杂度除了深度log2n以外,我们还需要临时数组,因此空间复杂度为O(n)=O(n)+O(log2n)。
运行结果
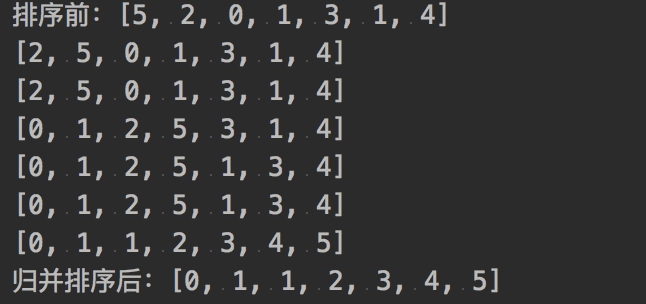
由于是递归,可能与理想输出有所差距。
基数排序
思想
将一组元素进行桶分配,啥意思?比如数字250,百位是2,十位是5,个位是0,而这些个位,十位等就是所谓的桶。
拆解分析

由于测试数据全是个位数,所以只要进行一次就结束了,如果有更高位的,将一直进行到最高位。
java代码实现
public static void radixSort(int[] array) {
int max = array[0];
final int length = array.length;
for (int i = 1; i < length; i++) {
if (array[i] > max) {
max = array[i];
}
}
int time = 0;//数组最大值位数
while (max > 0) {
max /= 10;
time++;
}
int k = 0; //重新放入数组的索引
int n = 1; //位值,如1,10,100
int m = 1; //当前在哪一位
int[][] temp = new int[10][length]; //数组的第一维表示该位数值,二维表示具体的值
int[] order = new int[10]; //数组order[i]用来表示该位是i的数的个数
while (m <= time) {
for (int num : array) {
int lsd = (num / n) % 10;//获取该位的基数0-9
temp[lsd][order[lsd]] = num;
order[lsd]++;
}
for (int i = 0; i < 10; i++) {
if (order[i] != 0) {
for (int j = 0; j < order[i]; j++) {
array[k] = temp[i][j];//基于m位的重新放入数组中
k++;
}
}
order[i] = 0;//复位
}
System.out.println("第" + m + "位排序:" + Arrays.toString(array));
n *= 10;
k = 0;//复位
m++;
}
System.out.println("基数排序后:" + Arrays.toString(array));
}直接给答案,最优时间复杂度为O(d(r+n)),最差时间复杂度为O(d(r+n)),平均时间复杂度为O(d(r+n)),空间复杂度为O(rd+n),其中r代表关键字基数,d代表长度,n代表关键字个数,由于是分配且从左往右,因此是稳定的。
运行结果

代码已经贴出来了,由于测试数据确实比较简单,大家可以自己使用复杂的原始数据进行测试。
总结
到这里,8种常见的排序算法介绍的差不多了,如果你心里想的是,卧槽,这么简单,我马上可以在我的小本本上写出来,那么我也没白写这篇文章。如果你是一脸懵逼,我心里可能想的是,卧槽,竟然没糊弄过去。哈哈,不管怎样,算法并不是什么高端的东西,其实你天天都在写算法,只不过。。。嘿嘿。算法可能有高低之分,但适合自己的才是最好的。尽量领会其中的思想,来完善你的算法吧。而这篇文章只不过是抛砖引玉,同我上篇文章带你领略clean架构的魅力,你看,是不是很多架构的文章?我发现我越来越自恋了,哈哈,但真的很希望更强的大佬能分享学习心得,我完全赞成打赏这种形式,甚至是你的小圈圈,但也得用点心啊。小弟,我心是用了,但是能力可能不足,如有错误,麻烦提出来,我及时修改。最后,感谢一直支持我的人!诶,差点没坚持下来。
哦,对了,我猜小伙伴又要吐槽我的作图,其实我觉得挺好的,不是吗?

传送门
Github:github.com/crazysunj/