本篇是二进制系列第三篇，如若你有兴趣，请持续关注，后期会持续更新。其他文章列表如下:

有趣的二进制

有趣的二进制—高效位运算

一、 精度

如果你有看过《有趣的二进制》这篇文章，你就会明白进制（不局限于二进制）中的小数是如何表示。因为每种进制都有其局限性，也就是约数的问题，比如

• 同样是1/3，在三进制下正好分干净，但在十进制下就总也分不完。十进制只能近似的表示1/3而无法精确的表示1/3。
  
• 同样是0.1，在十进制下可以精确的表示为0.1，而在二进制下只能近似的表示0.00011001100110011...(循环0011)
  

计算机中，存储数据的方式是采用二进制，因此在有限的存储空间下，绝大部分的十进制小数都不能用二进制浮点数来精确表示。一般情况下，你输入的十进制浮点数仅由实际存储在计算机中的近似的二进制浮点数表示。不要相信浮点数结果精确到了最后一位，也永远不要比较两个浮点数是否相等。

需要说明的是，虽然目前计算机表示的精度多数都是近似值，但多数情况下都够用了，如果你对精度有更高要求，每一种语言都有自己实现和处理方式。特别要注意的是防止上溢和下溢现象的发生。

二 、 IEEE 754 标准

1、IEEE 754

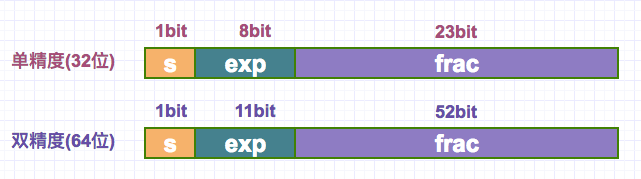
IEEE二进制浮点数算术标准（IEEE 754）是20世纪80年代以来最广泛使用的浮点数运算标准，为许多CPU与浮点运算器所采用。主要规范如下:

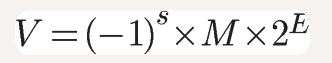
这个公式中:

1. s(Sign)：符号，表示是正数还是负数。0正数，1负数
   
2. E(Exponent)：指数域，E是2的指数，类似于科学计数法中（a×10^n）中的n，如此E是负数就可以表示小数了。不过这里E是一个无符号整数，32位的时候，E的占用8位，取值范围0-255，存储E的时候我们称为e，它是E的值与一个固定值（32位的情况是127）的和（e=E+bias,E=e-bias，bias=127）。采用这种方式表示是因为，指数的值可能为正也可能为负，如果采用补码表示的话，符号位S和Exp自身的符号位将导致不能简单的进行大小比较。
   
3. M(Mantissa):尾数域，浮点数具体的数值. 1≤M<2,隐含的以1开头表示，M表示的二进制表达式为1.xxx...,第一位总是1，因此IEEE 754规定，保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的xxxxxx部分。
   

2、示例

比如十进制的3.25，我们分为以下几步进行转换。

1、转换二进制

3.25 这整数部分3转换为二进制是11，小数部分0.25 转换为二进制为2^-2，也可以按照乘以 2 取整数位的方法:

(1) 0.25 x 2 = 0.5  取整数位 0 得 0.0
(2) 0.5 x 2 = 1  取整数位 1 得 0.01

如此3.25转化为二进制为11.01

2、有效数（Mantissa）

上述规则我们知道，尾数部分

最高有效位

（即整数字）是1，也就是尾数有一位隐含的二进制有效数字。因此我们转换尾数的时候，始终保持最高位为1（小数点左边），通过二进制科学计数法转换，我们得到11.01=1.101*2^1。

3、IEEE 754 规约形式

通过上述2步，得到1.101*2^1。我们采用规约形式获取填充3个部分

s(Sign）：正数=0；

E(Exponent):E=1,e=E+bias=1+127=128。此处存储的e，是经过以127作为偏移量调整的。

M(Mantissa):1.101 中，我只获取有效数（舍去整数部分1，只取小数部分）101

因此存在计算机中的3.25 浮点数是:

3、特殊值

从wiki上可以看到依据指数是否为0 ，还可以分为一下几种情况

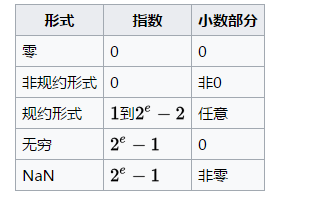
指数不全为0或者不全为1。此时为规约形式，如上述的示例。尾数部分，默认整数部分是1，不存储，获取后第一位默认为1。指数部分有偏移量

E全为0 。此时为非规约形式。为何要引入非规则浮点数，当小于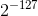的数会下溢为0，对于高精度来说这是不能接受的，而引入不规则浮点数后，小于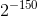的数才会下溢为0 。

E全为1 。尾数为0，则表示无穷大。非零则表示NaN(浮点数排序这种特殊问题需要处理)

4、运算方式

一般浮点数的运算流程如下，非规则浮点计算加法时“对阶”计算有不同，不再细说。

1. 指数项对齐。指数项对齐，小的向大的对齐，如果判断大小，则上述指数中的偏移量就起很大作用了，指数大的必然大，后续可以减少判断
2. 尾数求和。对齐后，对尾数进行加减处理
3. 规则化。对尾数进行截取，保证精度
4. 舍入。判断丢失的数值，进行舍入
5. 判断结果。判断结果是否溢出

三、非规范化浮点数

1、为何要引入非规范化浮点数

引入一个精度失准的事故:

On 25 February 1991, a loss of significance in a MIM-104 Patriot missile battery prevented it intercepting an incoming Scud missile in Dhahran, Saudi Arabia, contributing to the death of 28 soldiers from the U.S. Army’s 14th Quartermaster Detachment.[25] See also: Failure at Dhahran

1991年2月25日，在MIM-104爱国者导弹电池中，一个重要的精准丢失阻止了它在沙特阿拉伯达哈兰拦截一架新的飞毛腿导弹，造成美军第十四军区分离队28名士兵死亡。

对于规则浮点数而言，指数项范围为01-FE（1到254），当小于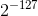的浮点数，用规格化数值表示，运算的时候会被电脑当作0来处理，如果精度能够再次提高一些的话，就不会出现这种情况了,因此引入不规则浮点数后，小于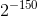的数才会下溢为0 。

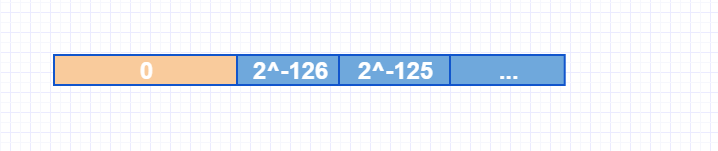
采用非规约浮点数，用来解决填补绝对值意义下最小规格数与零的距离，如上图所示，仅仅用规则浮点数的表示方式，0到最小正常数之间的间隔要远远大于最小正常数到次小正常数之间的间隔（2^-126 * 2^-23 = 2^-149），可以说是非常突然的下溢出到0，这是不满足我们的期望的。因此选择约定小数点前一位可以为0，剩下的一小段区间（即黄色括号）再均匀划分为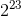段，如此就多了2^23精度，可以精确到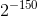附近。

2、引入非规范化浮点数带来的问题

在《你应该知道的浮点数基础知识》引入一个算法题，很好了诠释导致计算速率方面的问题。我简单贴一下:

 const float x=1.1;
 const float z=1.123;
 float y=x;
// 算法1  
 for(int j=0;j<90000000;j++)
    {
        y*=x;
        y/=z;
        y+=0.1f;
        y-=0.1f;
    }

// 算法2
for(int j=0;j<90000000;j++)
    {
        y*=x;
        y/=z;
        y+=0;
        y-=0;
    }

算法2中在进行上百次循环以后，y被标识为非规格化浮点，最终导致的结果是算法2比算法1慢了整整7倍左右。

这就是非规则浮点数的计算速度慢于规则浮点数，虽然下溢下沉了，但需要CPU额外进行解码和编码标识，如此，效率缓慢，极端情况下，规格化浮点数操作可能比硬件支持的非规格化浮点数操作快100倍。

另外非规则浮点数无法解决计算过程中下溢的产生，因为只是精度精确到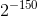附近，当有更小的浮点数时候，依然会下溢为0。