本文作者:Udacity深度学习&机器学习导师 Walker
题记:“简单” “形象” 两个要求我争取下。“有趣”的话,我觉得数学挺有趣的,你觉得呢?
神经网络是什么?神经网络就是一系列简单的节点,在简单的组合下,表达一个复杂的函数。下面我们来一个个解释
线性节点
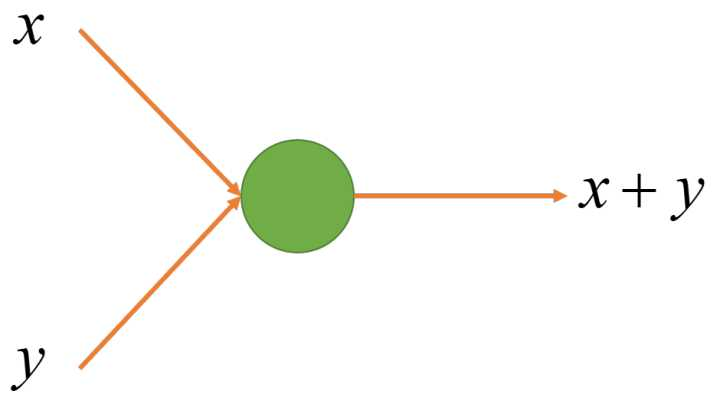
节点是一个简单的函数模型,有输入,有输出。我们
1. 最简单的线性节点: 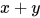
我能想到的最简单的线性节点当然就是 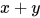 了。
了。
2. 参数化线形节点: 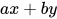
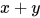 是一个特殊的线形组合,我们可以一般化所有
是一个特殊的线形组合,我们可以一般化所有 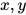 的线性组合, 即
的线性组合, 即 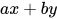 。这里
。这里 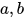 就是这个节点的参数。不同的参数可以让节点表示不同的函数,但节点的结构是一样的。
就是这个节点的参数。不同的参数可以让节点表示不同的函数,但节点的结构是一样的。
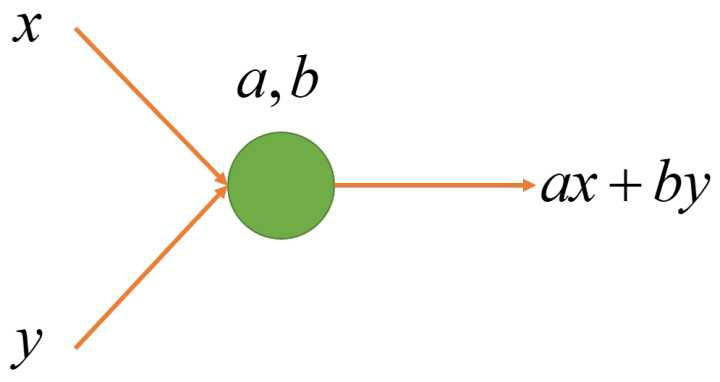
3. 多输入线性节点: 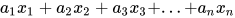
我们进一步把 2 个输入一般化成任意多个输入。这里 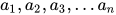 是这个节点的参数。同样,不同的参数可以让节点表示不同的函数,但节点的结构是一样的。注意
是这个节点的参数。同样,不同的参数可以让节点表示不同的函数,但节点的结构是一样的。注意 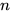 并不是这个节点的参数,输入个数不同的节点结构式不一样的。
并不是这个节点的参数,输入个数不同的节点结构式不一样的。
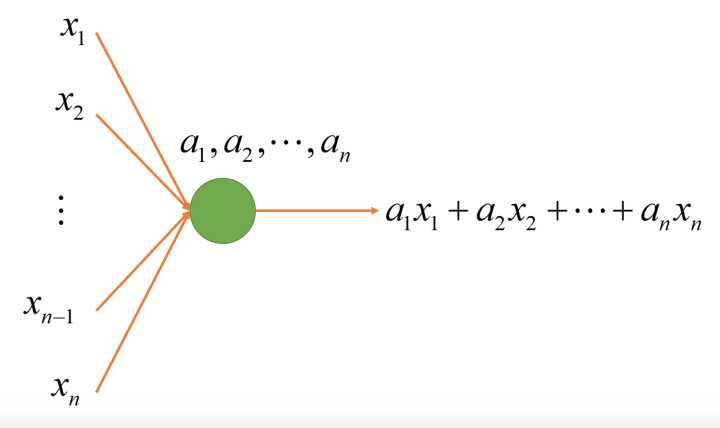
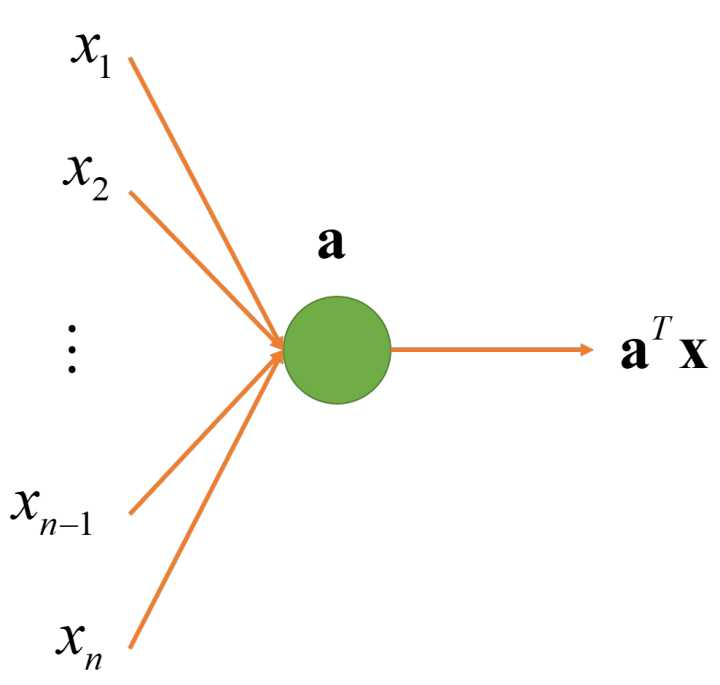
4. 线性节点的向量表达: 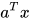
上面的式子太过冗长,我们用向量 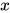 表示输入向量
表示输入向量 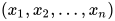 ,用向量
,用向量 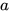 表示参数向量
表示参数向量 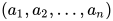 , 不难证明
, 不难证明 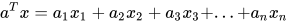 . 这里向量
. 这里向量 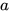 就是这个节点的参数,这个参数的唯度与输入向量的唯度相同。
就是这个节点的参数,这个参数的唯度与输入向量的唯度相同。
6. 带常量的线性节点: 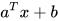
有时, 我们希望即使输入全部为 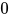 的时候,线形节点依然可以有输出,因此引入一个新的参数
的时候,线形节点依然可以有输出,因此引入一个新的参数 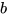 作为偏差项,以此来增加模型的表达性。有时,为了简化,我们以为会把表达式写作
作为偏差项,以此来增加模型的表达性。有时,为了简化,我们以为会把表达式写作 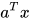 。此时
。此时 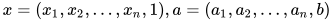
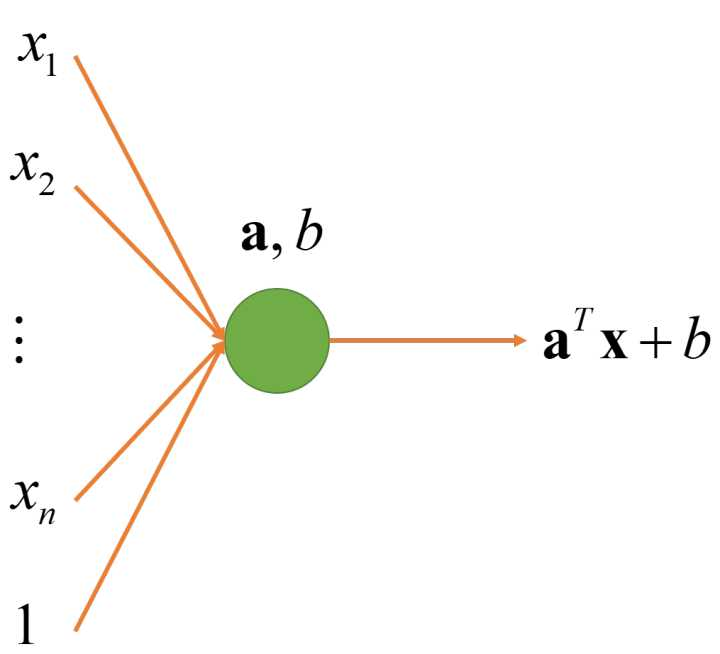
7. 带激活函数的线性节点: 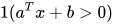
对于二项分类问题,函数的输出只是真或假,即 0 或 1。函数 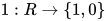 将真命题映射到 1, 将假命题映射到 0。
将真命题映射到 1, 将假命题映射到 0。
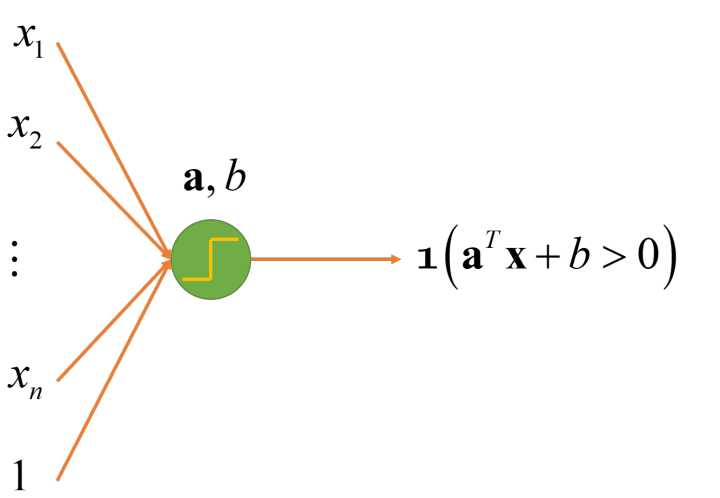
线性节点实例
1. 用线性节点表达 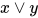 (或函数)
(或函数)
或函数的真值表如下:
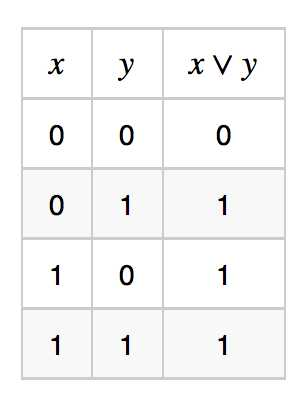
定义节点 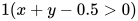 , 不难验证,它与
, 不难验证,它与 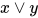 是等价的。
是等价的。
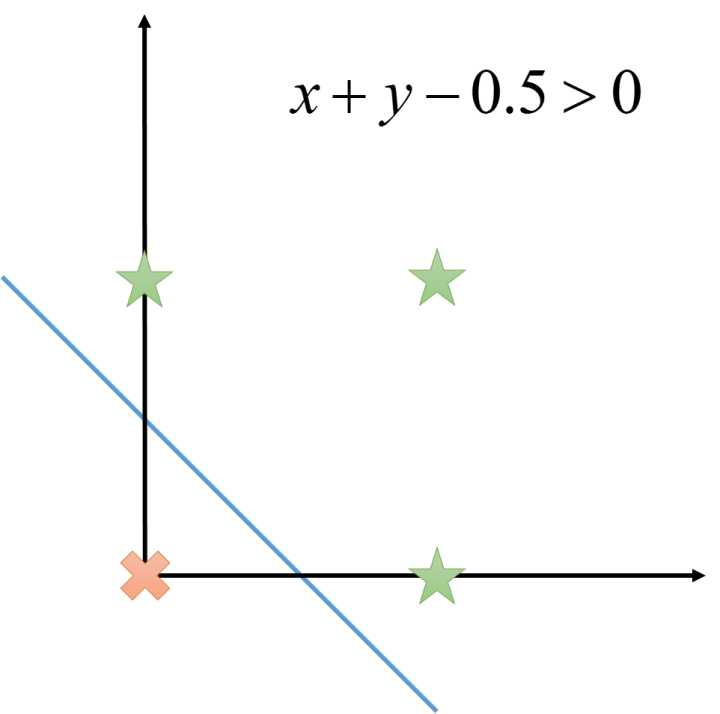
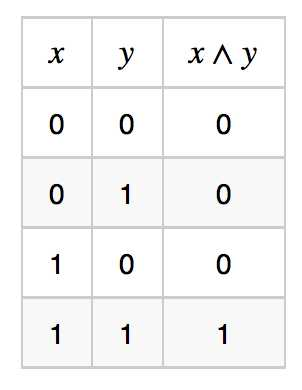
2. 用线性节点表达 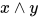 (与函数)
(与函数)
与函数的真值表如下:
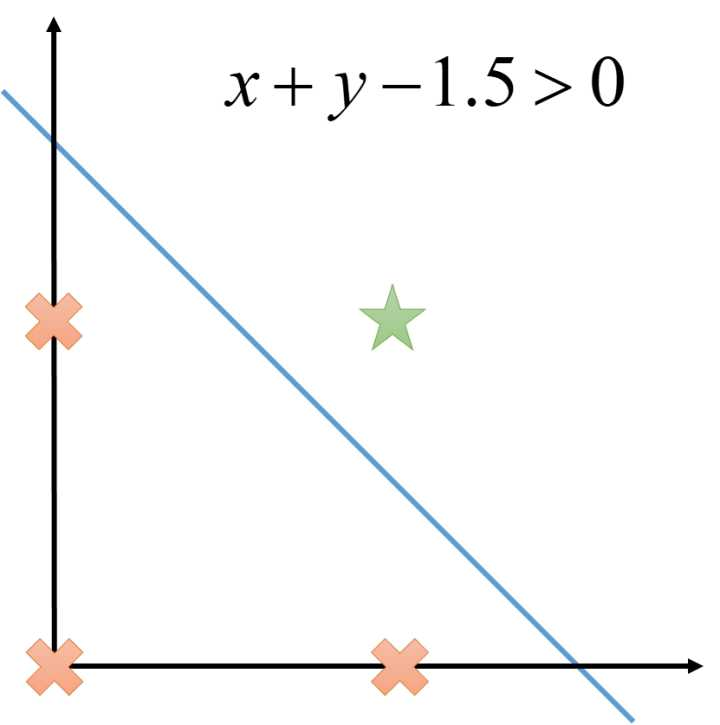
定义节点 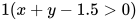 , 不难验证,它与
, 不难验证,它与 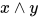 是等价的。
是等价的。
线性节点的表达力
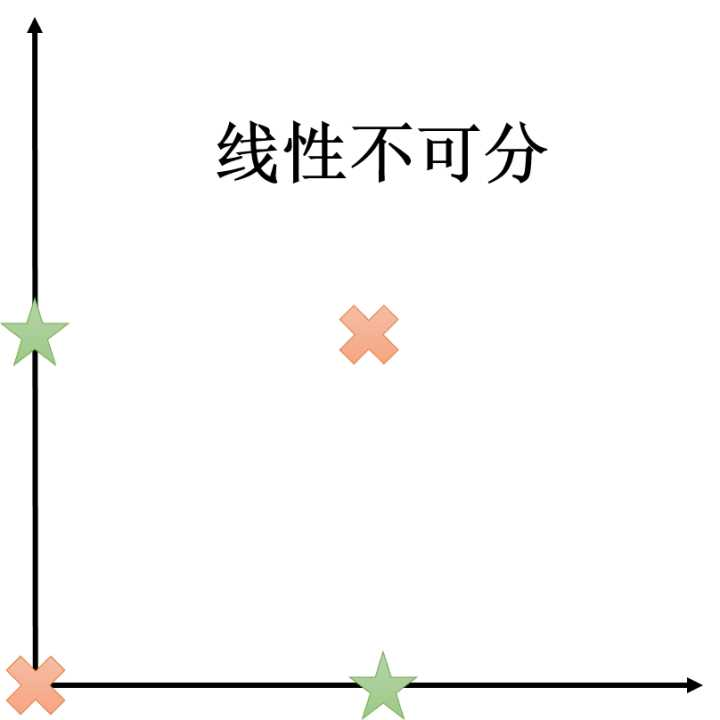
单个线性节点可以表达所有线性函数(函数值域为实数集)以及所有线性可分的分类器(函数值域为 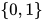 )。概念定义和命题的证明我们这里不在阐述。虽然单个线性节点已经很强大,但依然有他的局限性。对于线性不可分的函数,它无能为力,例如异或函数
)。概念定义和命题的证明我们这里不在阐述。虽然单个线性节点已经很强大,但依然有他的局限性。对于线性不可分的函数,它无能为力,例如异或函数 
线性节点的组合
1. 多个线性节点同层组合: 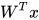
上述的线性节点输入是多维的,但输出只是一维,即一个实数。如果我们想要多维的输出,那么就可以并列放置多个节点。设 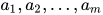 分别是
分别是 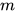 个节点的参数,那么输出则分别为
个节点的参数,那么输出则分别为 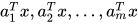 . 最终的输出结果为
. 最终的输出结果为
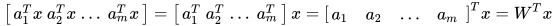
其中 ![W = [a_1, a_2, ... , a_m]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2017/11/30/1600c147c016f827~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) 是一个
是一个 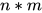 的参数矩阵。
的参数矩阵。
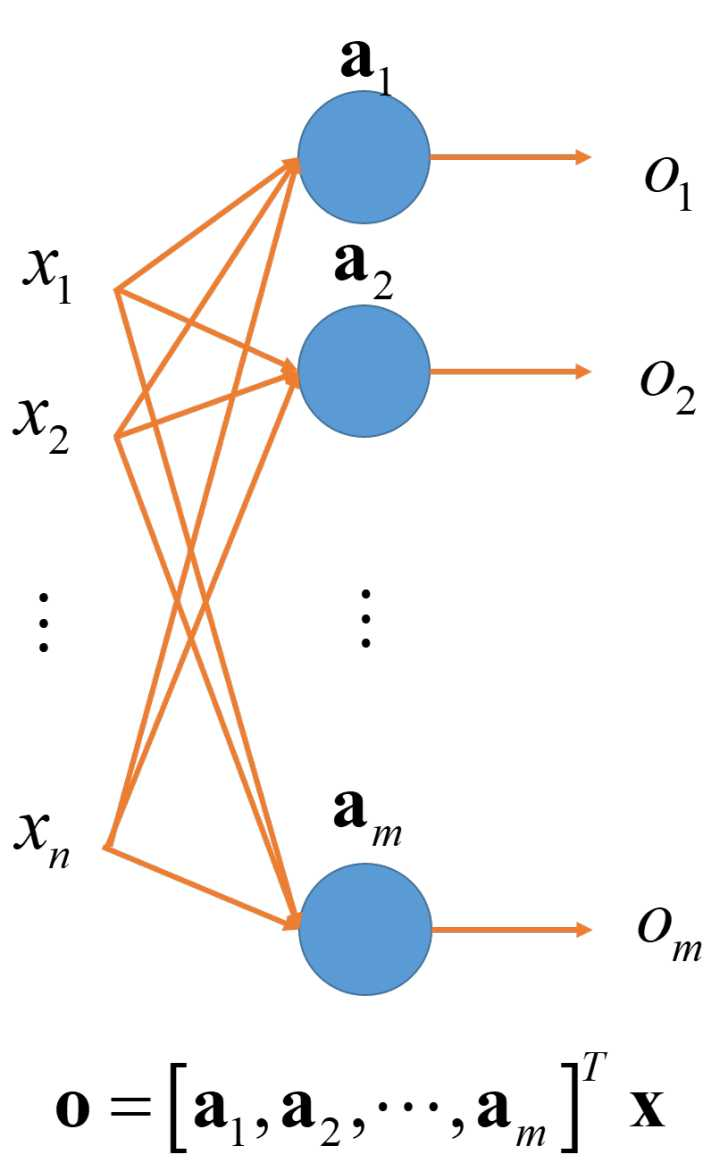
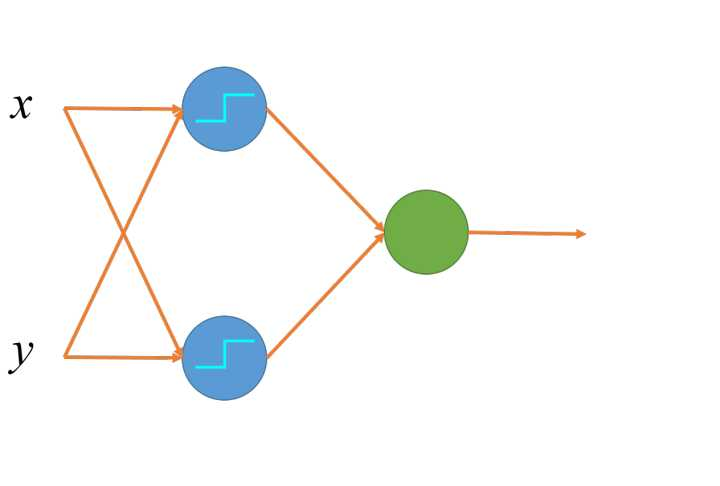
2. 多层线性节点:
多层线性节点中,某一层带激活函数的线性节点,输出作为下一层的输入。通常中间层(或者隐藏层,图中的蓝色节点)会带有一个激活函数,来增加模型的表达力。(思考: 如果隐藏层没有激活函数,为什么两层线性节点和一层等价?)
多层多层线性节点实例
1. 用多层表达异或函数 
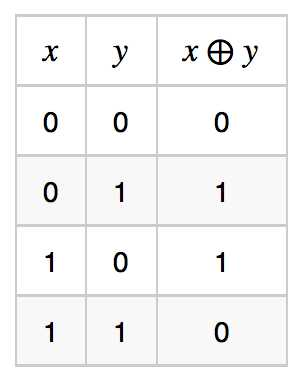
这是一个不可线性分隔的函数,不可以用一个线性节点表达。但我们可以使用多层的线性节点来完成这个任务。
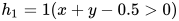 或
或 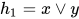
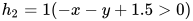 或
或 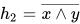
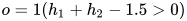 或
或 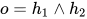
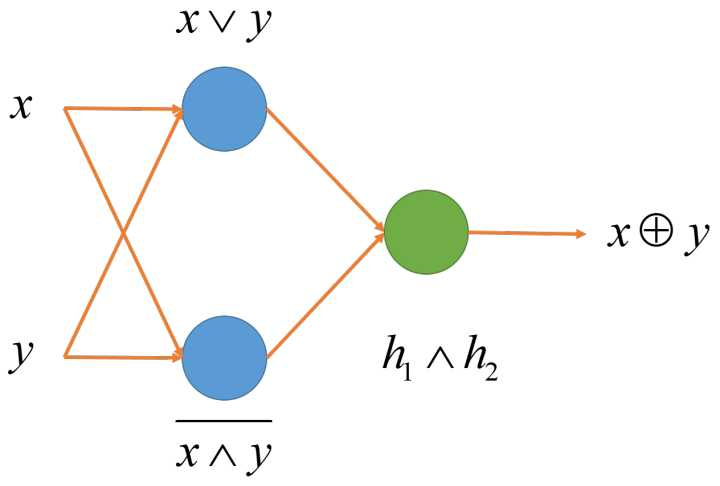
多层线性节点的表达力
可以证明,多层神经元可以表达所有连续函数。证明比较复杂,有兴趣的人可以去看一下: A visual proof that neural nets can compute any function
写到这里差不多基本讲清楚了神经网络的计算方式,但其实我们还有很多常见的节点没有讲到,例如 Relu, Sigmoid, Dropout 等。神经网络不止有正向计算,还有反向传导,这些节点的出现和反向传导息息相关,有机会的话,再来写一篇文章回答 如何简单形象又有趣地讲解神经网络的反向传导?
如果大家想深入学习更多关于神经网络的知识,也可以参考来自硅谷前沿技术学习平台 优达学城 (Udacity)的深度学习课程,里面非常详细的讲解了你所想要的一切~