背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为： 给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。

问题

假设山洞里共有a,b,c,d,e这5件宝物（不是5种宝物），它们的重量分别是2,2,6,5,4， 它们的价值分别是6,3,5,4,6，现在给你个承重为 10 的背包, 怎么装背包，可以才能带走最多的财富。

动态规划

转化方程

动态规划一个关键的步骤是得到状态转化方程，物体的价值用 v(k) 表示， 重量用 w(k) 表示，f[i, j] 表示将前 i 个物体放入到容量为 j 的背包中的最大价值，则有:

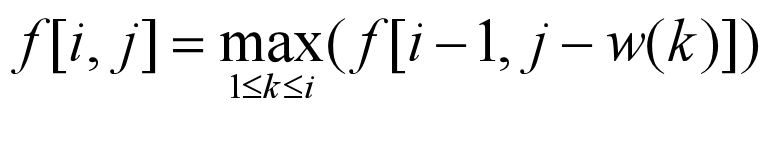
求解方法

动态规划有两种等价的实现方法：

1. 带备忘的自顶向下法。此方法按照自然的递归形式编写过程，但过程中会保存每个子问题的解（通常保存在一个数组或散列表中）。 当需要一个子问题的解时，过程首先检查是否已经保存过此解。如果是，则直接返回保存的值，从而节省了时间；否则，按通常方式计算 这个子问题。

2. 自底向上法。这种方法一般需要恰当定义子问题“规模”的概念，使得任何子问题的求解都只依赖于“更小的”子问题的求解。因而 我们可以将子问题按规模排序，按由小至大的顺序进行求解。当求解某个子问题时，它所依赖的那些更小的子问题都已求解完毕， 结果已经保存。

带备忘的自顶向下方法

下面给出一个带备忘的自顶向下实现：

var v = [6,3,5,4,6]
var w = [2,2,6,5,4]
var c = 10

function bag (v, w, c) {
  function _bag (v, w, c, f, s) {
    // 子问题的规模
    var n = v.length
    // 子问题已经被求解
    if (f[n][c] > 0) {
      return f[n][c]
    }
    // 从剩下的物品中选择一件
    for (var i = 0; i < n; i++) {
      var newW = w.slice()
      newW.splice(i, 1)
      var newV = v.slice()
      newV.splice(i, 1)
      // 选出来的物品重量大于背包剩余容量，则该子问题的解为0
      if (w[i] > c) {
        return 0
      }
      // 否则递归求解，得到子问题的最大的解及当前选择的物品
      var maxValue = v[i] + _bag(newV, newW, c - w[i], f, s)
      if (f[n][c] < maxValue) {
        f[n][c] = maxValue
        s[n][c] = {v: v[i], w: w[i]}
      }
    }
    // 返回子问题的最大解
    return f[n][c]
  }

  var n = v.length
  // 记录最大的价值
  var f = []
  // 记录每一步所做的选择
  var s = []
  for (var i = 0; i <= n; i++) {
    f[i] = []
    s[i] = []
    for (var j = 0; j <= c; j++) {
      f[i][j] = 0
      s[i][j] = null
    }
  }
  _bag(v, w, c, f, s)

  // 打印两个二维数组
  console.log(f)
  console.log(s)

  // 从s中得到所选择的物品
  var selected = []
  var i = n
  var j = c
  var sum = 0
  do {
    var thing = s[i][j]
    if (thing) {
      selected.push(thing)
      j -= thing.w
      i--
    }
  } while (thing)

  return {
    maxV: f[n][c],
    selected: selected
  }
}

说明

程序中 f 最后如下所示，其中第一行可以忽略，这么做只是为了让数组索引从 1 开始，跟上面的公式保持一致：

0	1	2	3	4	5	6	7	8	9	10
null	null	null	null	null	null	null	null	null	null	null
null	null	null	null	null	null	null	null	null	null	null
0	0	0	null	null	null	null	null	null	null	null
0	0	0	0	0	null	6	null	null	null	null
null	null	null	null	6	6	6	null	9	null	null
null	null	null	null	null	null	null	null	null	null	15

其中，f[5][10] 就是最后所求的最大价值，即 15。 从上表还可以知道求解过程中递归求解了哪些问题，即上表中值不为 null 的那些。 而如果需要知道最后所选择的物品，还需要借助 s :

0	1	2	3	4	5	6	7	8	9	10
null	null	null	null	null	null	null	null	null	null	null
null	null	null	null	null	null	null	null	null	null	null
null	null	null	null	null	null	null	null	null	null	null
null	null	{ v: 3, w: 2 }	{ v: 3, w: 2 }	{ v: 3, w: 2 }	null	{ v: 6, w: 4 }	null	null	null	null
null	null	null	null	{ v: 6, w: 4 }	{ v: 6, w: 4 }	{ v: 6, w: 2 }	null	{ v: 3, w: 2 }	null	null
null	null	null	null	null	null	null	null	null	null	{ v: 6, w: 2 }

其中，s[i][j] 表示将前 i 个物体放入到容量为 j 的背包中时所选择的第一个物品

现在，让我们来理一下这个过程：

1. s[5][10] 表示将前 5 个物品放到容量为 10 的背包中，选择了物品 { v: 6, w: 2 }
2. 接下来处理子问题 s[4][8] ，选择了物品 { v: 6, w: 4 }
3. 接下来处理子问题 s[3][4] ，选择了物品 { v: 3, w: 2 }
4. 接下来处理子问题 s[2][2] ，没有选择任何物品。
5. 得到最后所选择的物品为 { v: 6, w: 2 }, { v: 6, w: 4 }, { v: 3, w: 2 }

自底向上法

下面是自底向上法的实现：

function bag2 (v, w, c) {
  var f = []
  var s = []
  var n = v.length

  for (var i = 0; i <= n; i++) {
    f[i] = []
    s[i] = []
    for (var j = 0; j <= c; j++) {
      f[i][j] = 0
      s[i][j] = 0
    }
  }

  // 遍历物品
  for (var i = 1; i <= n; i++) {
    var index = i - 1
    // 遍历容量
    for (var j = 0; j <= c; j++) {
      // 当前物品放入的情况
      if (w[index] <= j && v[index] + f[i - 1][j - w[index]] > f[i - 1][j]) {
        f[i][j] = v[index] + f[i - 1][j - w[index]]
        s[i][j] = 1
      }
      // 当前物品不放入的情况
      else {
        f[i][j] = f[i - 1][j]
      }
    }
  }

  return{
    f: f,
    s: s
  }
}

说明

首先，注意到这个事实：物品放入的顺序不会影响我们最后的结果。这里按照题目中的顺序依次考察 每个物品在每个容量的情况下是否放入。

仍然用 f 来记录最大值，用 s 来记录选择。

不过这里的 s[i][j] 只需标记当前物品是否放入即可， 所以 s[i][j] 取值为 0 或 1。

f 如下所示:

v	w	0	1	2	3	4	5	6	7	8	9	10
-	-	0	0	0	0	0	0	0	0	0	0	0
6	2	0	0	6	6	6	6	6	6	6	6	6
3	2	0	0	6	6	9	9	9	9	9	9	9
5	6	0	0	6	6	9	9	9	9	11	11	14
4	5	0	0	6	6	9	9	9	10	11	13	14
6	4	0	0	6	6	9	9	12	12	15	15	15

s 如下所示:

v	w	0	1	2	3	4	5	6	7	8	9	10
-	-	0	0	0	0	0	0	0	0	0	0	0
6	2	0	0	1	1	1	1	1	1	1	1	1
3	2	0	0	0	0	1	1	1	1	1	1	1
5	6	0	0	0	0	0	0	0	0	1	1	1
4	5	0	0	0	0	0	0	0	1	0	1	0
6	4	0	0	0	0	0	0	1	1	1	1	1

同样，我们可以反向推导出最后的选择：

1. s[5][10] 为 1，该物体放入袋中
2. 考察 s[4][6]，为 0，说明这个物体不放入
3. 考察 s[3][6]，为 0， 不放入
4. 考察 s[2][6]，为 1， 放入
5. 考察 s[1][4], 为 1， 放入
6. 得到最后所选择的物品为 { v: 6, w: 2 }, { v: 3, w: 2 }, { v: 6, w: 4 }

总结

以后碰到动态规划相关的问题都可以用这个思路来解决了，关键在于要构造转移函数这个模型。 个人感觉自顶向下法更加好理解，但是代码略显啰嗦了。