SVM
SVM 即支持向量机,常用于二分类模型。它主要的思想是:
- 它是特征空间上间隔最大的线性分类器。
- 对于线性不可分的情况,通过非线性映射算法将低维空间的线性不可分的样本映射到高维特征空间,高维特征空间能够进行线性分析。
结构风险
对于指定的损失函数,根据一定的样本集就能根据这些样本来计算经验风险,而经验风险最小化就是根据样本集来最小化经验风险。
假如我们能获取到所有数据,那么我们希望整个数据集的损失能越小越好,这就表示模型越好。但很多时候基本不可能获取到所有数据,这时就可以根据样本的联合分布P(X,Y)来计算期望风险:
可以看到当样本数趋于无穷大时,经验风险会趋于期望风险。实际情况下,我们的训练样本很有限,如果完全只考虑经验风险,则可能会出现过拟合现象,这时它能很好预测训练样本,但其泛化能力有限,对非训练数据预测能力可能不好。为了克服这个问题,引入了结构风险。
结构风险 = 经验风险 + 置信风险。置信风险可以是一个正则化项,这种做法叫正则化,正则化项与模型的复杂程度相关,复杂度越高则正则化的值越大。常用的正则化项是模型参数的范数。
此外,如果不使用结构风险,则可以使用交叉验证的思想来综合考虑所有训练出来的模型,越能准确预测验证集的模型就表示越好。
间隔最大化
从感性上理解支持向量机,如下图,假设有两种不同类别的数据,分布在空间上,支持向量机的任务就是找到一个划分超平面,将它们分割成两类,所以我们看到其实是不止存在一个超平面可以对其进行划分的,到底哪一个才是最好的呢?这就需要我们根据一定的约束条件去找出这个最好的超平面。
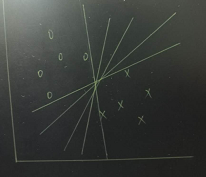
对于给定的样本集,其中
,它表示类标记,分别用+1和-1表示。我们设超平面对应方程为
其中w为法向量,b为位移项,超平面由法向量(决定方向)和位移项(决定超平面与原点距离)共同决定。那么样本对应的点到超平面的距离为,
在所有样本都能正确被超平面划分的情况下,则样本集T中,对于则有
,反之对于
则有
。
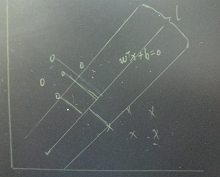
超平面两边分别存在离超平面最近的一些样本点(这些点称为支持向量),如图中中间的超平面向两边平移后得到两个超平面,对应的方差分别为
这两个超平面的距离即称为间隔,在这两个超平面的样本点到中间超平面的距离之和为
现在我们的任务是在约束条件下找到最大的间隔,即要找到w和b使得l最大,
其实就是最大化,等价于最小化
,于是上述优化问题变为,
解除该优化问题即得到最大间隔分离超平面。
对偶问题
上面的优化问题是凸二次规划问题,一般可用拉格朗日方法求解。首先引入拉格朗日函数,要求,
其中为拉格朗日乘子向量。
为求得对偶问题的解,需要先求拉格朗日函数对w、b的极小,再求拉格朗日函数对a的极大,即。
求极小则对w,b求偏导并令其为0,有
综合上述几个式子,将w代回原来的式子可以将w和b消掉,于是拉格朗日函数对a求极大变为,
解上述方程可以用二次规划算法求解,也可以用数值方法求解,或者用SMO算法。解得a后就能解得w和b。
另外,还有一个很重要的约束,,可以看到对于任意样本
,总满足
或
。当对应的拉格朗日系数为非0时,这个样本是一个支持向量,当对应拉格朗日系数为0时,这个样本不是支持向量,由此也可知大多数拉格朗日系数都是0,因为大多数样本都不是支持向量。
核函数
引入核函数的目的是为了解决线性不可分的情况,可以看到我们前面讨论的样本是属于线性可分的,而对于实际问题的样本可能并不能直接找到一个超平面将其划分成两类。如下图,无法一刀将样本切分开。
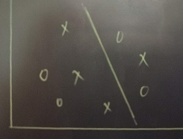
对于这种线性不可分的问题,可以将样本从原始空间映射到更高维度的 特征空间,这样在高维的特征空间就能线性可分。比如对于原来二维的空间就可以映射到三维空间去,而且在这三维空间可以找到划分的超平面。可以认为一定存在一个更高维的空间能映射原始空间,从而使其可分。
假设为映射后的特征向量,则在特征空间上讨论的模型变为,
同样求解对偶问题
继续假设函数
于是可以解得,
这里函数k就是核函数。
常用核函数包括线性核、多项式核、高斯核、sigmoid核等等。
-------------推荐阅读------------
------------------广告时间----------------
公众号的菜单已分为“分布式”、“机器学习”、“深度学习”、“NLP”、“Java深度”、“Java并发核心”、“JDK源码”、“Tomcat内核”等,可能有一款适合你的胃口。
鄙人的新书《Tomcat内核设计剖析》已经在京东销售了,有需要的朋友可以购买。感谢各位朋友。
欢迎关注:
