写在前面:我将从一个入门者的视角(水平)将机器学习中的常用算法娓娓道来。自身水平确实有限,如果其中有什么错误的话希望大家指出,避免误导大家。对于开篇有比较多的东西想说,所以另取一章介绍一下我个人对机器学习这个领域的理解和一些基本常识介绍。如果你时间比较充裕,可以看看我
前言的文字介绍。
0 前言
介绍一下个人想法
0.1 关于机器学习
毫无疑问,机器学习现在越来越热门了,需求随着以后人工智能大爆发会持续增长。不管你是不是这个编程领域的人,都有必要了解一下机器学习是怎么回事,至少有个理性的认识,而不是觉得很神秘。但是涉及到算法数学知识是可以忽略的,只要知道,我们通过某个数学手段可以达到某个目的。比如这里要介绍的线性回归在更新权重时是依据梯度下降算法的,你可以不必知道什么是梯度下降,知道知道数学上对于求解最优化是有自己的手段的,当然如果能知道更好。由于机器学习的性质,速成基本不太可能,而且现在处于高速发展的阶段,必须保持学习的热情才能学得下去。另外,这个前期的学习成本是比较高的,在自己写代码之前,要想心里有点底,至少要对 微积分、线性代数 和 概率论 的应用要有点自己的理解的。所以这也是一大优势,不太容易被取代。
0.2 关于线性回归
对于理性了解机器学习的捷径就是弄懂线性回归算法的整个流程,如果你通过这篇文章真的理解了线性回归,那么你应该就理解这句话了。当然,对于大多数阅读者篇文章的人来说,可能早就对线性回归有了自己的理解。但是我这要提的是,如果你没打算入门机器学习,阅读一下线性回归也是对自己知识面进行拓展的一个好方式,因为基本大多数人都是从这里开始的。
0.3 关于基础
首先,你需要一点 基础。如果没有也简单,自学一下就行。然后就是要学习一下以下工具的使用:
NumPy,Matplotlib,sklearn,TensorFlow。其中部分可以参考我以前的文章。
有了这些你还需要一些数学基础。数学的话我觉得不要求全学会,也不太现实,可以在写代码过程中碰到什么算法再去寻求数学证明,前提是之前的知识量最好能达到看懂大多数数学知识的水平。这里我觉得知乎上有些数学科普其实挺不错的,毕竟不是数学系,所以理解主要逻辑之后持有一种拿来用的态度我觉得没问题。
0.4 关于参考
这里很感谢像吴恩达、莫烦等老师的无私奉献,还有很多在网上写博客分享知识的人,让编程这个行业形成一个良好的学习风气。而且网上还流传很多优质的学习资源,所以这里我将我学习过程的参考资料整理进了 GitHub,我想大家奉献出来就是为了别人更好的学习吧,如果有侵权之类的话,我会立即删除的。然后这一系列的文章,我会主要以吴恩达老师的课程为基础,以初学者的视角记录并且实践。
0.5 关于我
一个即将毕业的知识水平有限的本科生,所以文章肯定有很多不足之处,望大家指正。然后实验的代码在这里。
1 背景
故事就不讲了,可以参考视视频。下面我讲讲这个是要解决什么问题?生活中往往有很多现象,而我们可以从现象总结出某些结论,但是,如果我们看到了一个之前从来都没有看到过的现象,我们就无法下结论了。但但是一些有经验的人可以凭借丰富的经验进行预测。就比如,一个处于懵懂期的小孩子,看见一片乌云不能推测出会下雨,而一个大人就会知道,提醒小孩出门要带伞。。。好吧,还是在讲故事,那就继续吧😂😂😂。这个例子中的大人小孩的区别在于年龄不同,见识不同,知识水平自然不同,能做出的判断也自然不同。所以要想达到对现象进行预测,那么就必须进行学习,等小孩慢慢长大了,看到蚂蚁搬家就会带伞出门了。
好了,我们总结一下上面的故事:现象可以比喻成数据,结论造成的行为也是数据,唯一不同的是,是由现象得出的结论,所以可以将现象的数据看作是输入,结论的数据看成是输出。那么机器学习就是将输入数据输入进一个模型,然后将模型的输出结果和之前的“正确”结论作比对慢慢更改模型,直到这个模型对出入数据有较好的预测,那么这个模型就可以拿来用了。抽象出来的话就是找一个输入 和输出
之间的映射
,使得对于绝大多数
都能通过映射
较好地得到
。
房价的例子我就不举了,直接看下面的图,看看能不能解决
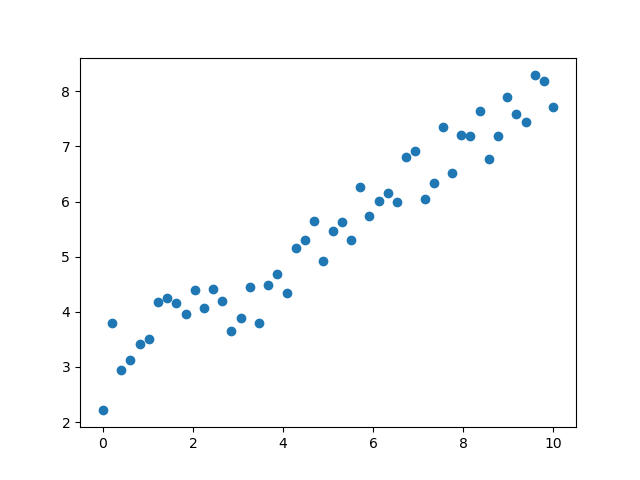
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
def draw():
X = np.linspace(0, 10, 50)
noise = np.random.normal(0, 0.5, X.shape)
Y = X * 0.5 + 3 + noise
plt.scatter(X, Y)
plt.savefig("scattergraph.png")
plt.show()
if __name__ == "__main__":
draw()
好了,你可能会发现,要想给出 依赖的是直觉,所以每一个人的答案都是不一样的,而对于某些标准统一的领域(比如军事项目),这种依靠直觉判断的情况绝对不容许发生。想象在现代信息化战场上靠直觉怎么可能作战成功?
所以我们需要一个模型,你可以理解成一个黑盒,把 喂进去,把
取出来,而且无论谁,只要那个黑盒是同一个,那么每个人的输入
相同的话,输出
就是相同的。 那么在这里这个模型大概是什么形状的呢?目前这个还是我们人为干预进行选择的。直观来说,可以这个分布看成一条很粗的线,那么我们选择线性模型来模拟分布。那么如何确定这个线性模型呢?这里就涉及到今天的主角:线性回归
2 一元线性回归
先从一元线性函数开始分析,既然假设是一元线性,那么我们的拟合函数就可以定义为 了。同样那前一个图作为例子,我们现在的目的是求出
,如果求出来了,给定任意一个
就能求出
来了。
2.1 定义评估函数-损失函数
这里讲解如何求出 的整个思考过程。
我们选取一个点 因为误差的存在,所以
。同理如果有很多点,那么就有以下结果,为了方便,我们取评估值
。
我们的目的自然是误差越小越好,所以采用平方和的形式表达误差:
到这里,我们来看看图像是怎么样的?
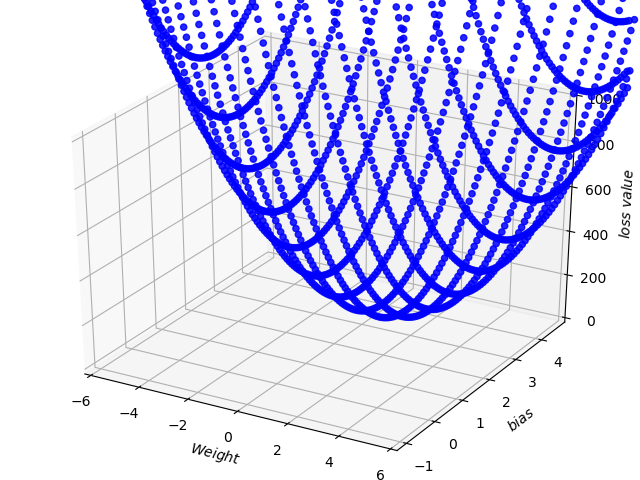
PS:图有点丑,实在是没办法了,设置了噪点,使得函数值跨度很大,稍微改一下就会呼脸。只能设置散点图凑合看了,望知道的小伙伴告知。好了,就不在这浪费过多时间了,直接看代码。
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)
ax.set_xlabel(r'$Weight$')
ax.set_ylabel(r'$bias$')
ax.set_zlabel(r'$loss\ value$')
N = 200
X = np.linspace(0, 10, N)
noise = np.random.normal(0, 0.1, X.shape)
Y = X * 0.5 + 3 + noise
W = np.linspace(-10, 10, N)
b = np.linspace(-2, 8, N)
p = 0.6
plt.xlim(W.min() * p, W.max() * p)
plt.ylim(b.min() * p, b.max() * p)
ax.set_zlim(0, 1000)
h = []
for i in W:
for j in b:
h.append(np.sum(np.square(Y - (X * i + j))))
print(np.min(h))
h = np.asarray(h).reshape(N, N)
W, b = np.meshgrid(W, b)
ax.scatter(W, b, h, c='b')
plt.savefig("lossgraph.png")
plt.show()
现在我们通过可视化的手段知道了大概什么位置取最小值,其实我们还是没有达到目的,我们要的是 具体值。
2.2 求解最小值-梯度下降
问题被进一步细化,就是求解下面二元函数在什么时候取极值:
这时候高数就登场了,找了一张图

那问题就很简单了,就是直接求对 的偏导等于
的方程组。但是这是数学方法,不符合计算机思维,就好像我们解一个一元一次方程,普通方法是直接拿定义域内的值一个一个试,直到结果符合预期。当然,高级一点点的方法是可以写一个解释器,把人类计算方法程序化。显然这里不太现实,而且方程类型一变,解释器很可能就不适用了。所以我们还是采用那种机器认可的“笨”办法,想起开学时计算机导论老师评价计算机的一句话:
fast but stupid。说明在这种情况下,我们可以接受用快来弥补其它劣势,只要计算的值一步一步靠近最终结果就能满足需求。其实说到这里,计算机变快的这些特点和现在机器学习、人工智能领域的兴起有一定关系。
好了,下面开始想一个办法如何让结果慢慢趋近与极值。
我们可以这样想,随机放一个球在这个平面上,等到球禁止时,它所在的位置就是极值的位置。那我们如何模仿这一过程呢?
第一步:放球
这个好做,就是直接随机一个在定义域内的任意位置就好了。
第二步:滚动
滚动的话如何去模拟是一个比较难的点,但是仔细分析就很好理解了。你可以把自己想象成那个球,开始站在某个地方,这个地方很不稳,那么你自然反应肯定是往平整的地方去,前提是每个位置的海拔差不多。那这样就说明那些斜率越大的地方有更大的几率更快跌落谷底。这个例子有个不恰当的地方,可以思考下二次函数,这里主要是体会这种思维,而我们是可以变通的。当你有了这种斜率的思维,那就好办了,下面给出总结:我们总是希望在给定步长的情况下,往水平最低的地方行进。而其中要知道那个是最低,又是一个难题,计算机可没有直觉,如果数值设置不当,可能导致函数收敛过慢或者直接发散,而这些都是机器学习应该极力避免的。
为了好分析问题,我们采用控制变量方法。可以看到,在损失函数中有两个变量 ,当
取某一值得时候,
是一个二次函数。
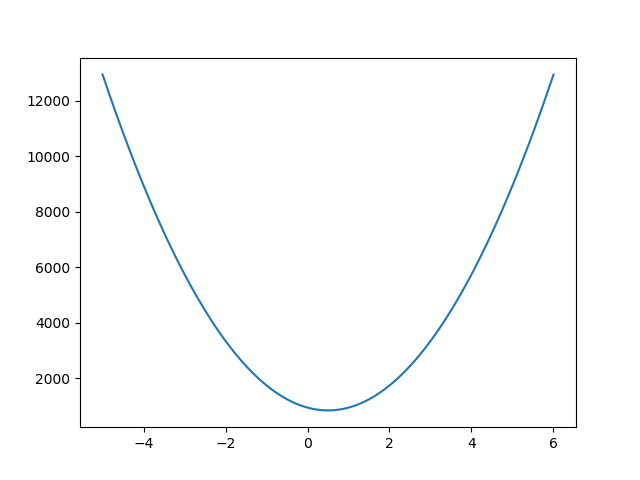
# coding: utf-8
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure()
N = 200
X = np.linspace(0, 10, N * 2)
noise = np.random.normal(0, 0.1, X.shape)
Y = X * 0.5 + 3 + noise
W = 1
b = np.linspace(-5, 6, N)
h = []
for i in b:
h.append(np.sum(np.square(Y - (X * W + i))))
plt.plot(b, h)
plt.savefig("quadraticFunction.png")
plt.show()
我们来直接看吴恩达老师的课件吧,有点不想做图了。。。
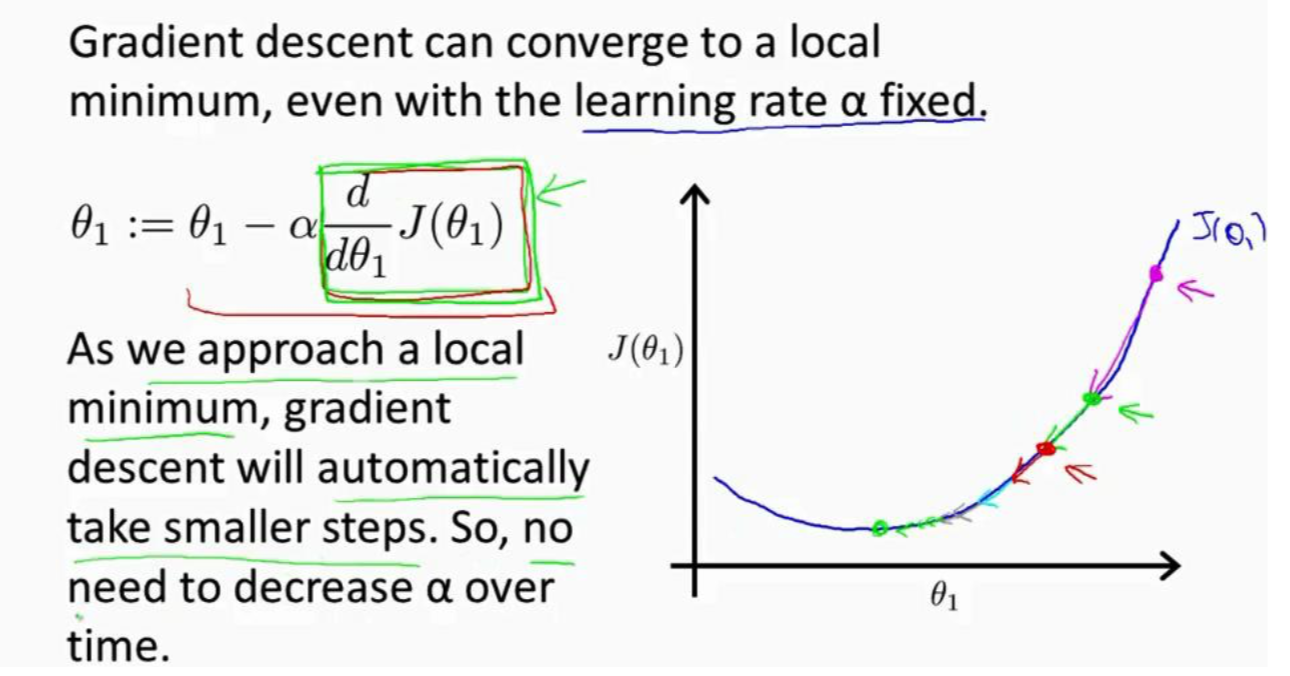
现在我们可以引出更新规则了,在这里求解最小值,对于一元函数来说就是求导,对于多元函数就是求偏导了。很明显,当斜率为正的时候,我们要往负反向走,反之往正方向走。所以我们可以加上一个关于斜率呈反比的函数来跟新值,至于更新力度也就是前面说的一次走多远就是学习率的设定了。而且离极值点越远,斜率绝对值越大,步子迈得越大,符合更新逻辑。
这里可能有点思维跳跃的是除了一个 ,可以从数据量的角度思考,也可以从更新斜率的角度思考,因为在更新权重中,我们不仅仅只是计算一个点的斜率,如果直接求和必定会导致权重过大从而最终结果是发散的,这点大家可以自己改改代码试试。好了,既然基本思路都出来了,那就写代码实现吧。
# coding: utf-8
import matplotlib.pyplot as plt
import numpy as np
N = 200
X = np.linspace(0, 10, N * 2)
noise = np.random.normal(0, 0.5, X.shape)
Y = X * 0.5 + 3 + noise
def calcLoss(train_X, train_Y, W, b):
return np.sum(np.square(train_Y - (train_X * W + b)))
def gradientDescent(train_X, train_Y, W, b, learningrate=0.001, trainingtimes=500):
global loss
global W_trace
global b_trace
size = train_Y.size
for _ in range(trainingtimes):
prediction = W * train_X + b
tempW = W + learningrate * np.sum(train_X * (train_Y - prediction)) / size
tempb = b + learningrate * np.sum(train_Y - prediction) / size
W = tempW
b = tempb
loss.append(calcLoss(train_X, train_Y, W, b))
W_trace.append(W)
b_trace.append(b)
Training_Times = 100
Learning_Rate = 0.002
loss = []
W_trace = [-1]
b_trace = [1]
gradientDescent(X, Y, W_trace[0], b_trace[0], learningrate=Learning_Rate, trainingtimes=Training_Times)
print(W_trace[-1], b_trace[-1])
fig = plt.figure()
plt.title(r'$loss\ function\ change\ tendency$')
plt.xlabel(r'$learning\ times$')
plt.ylabel(r'$loss\ value$')
plt.plot(np.linspace(1, Training_Times, Training_Times), loss)
plt.savefig("gradientDescentLR.png")
plt.show()
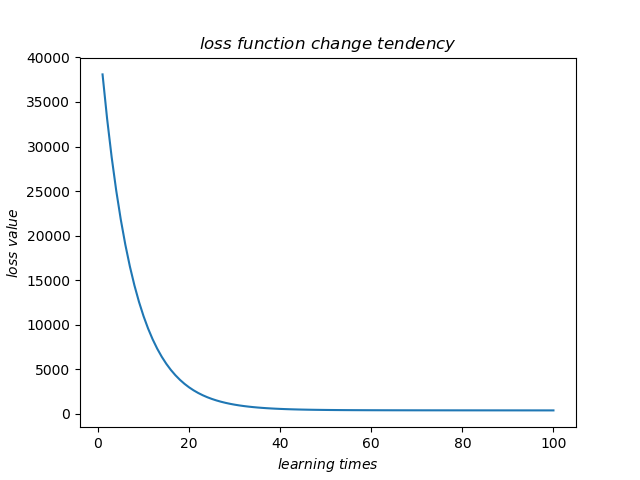
到这里,我们基本手写实现了一元变量的线性回归,这里为了方便训练次数取得比较少,只有 次,这远远不够,我测试了一下,大概达到
次训练效果就比较好了。当然也可以调整学习率,初始值……读者可以自行尝试。
3 多元线性回归
这里我们先拆分理解多元代表多个自变量,线性代表自变量之间满足齐次性和可加性,回归就是一种方法的表述。一元好办,我们可以通过各种工具实现可视化,但是多元的表述就有了一些困难,特别是在高维线性空间我们想象不出来。所以我们就必须抽象出来,使用数学符号代替那些复杂的变量。
可能你已经想到了,对,没错,我们要使用线性代数了。如果之前没有一点基础的话,可以稍微花点时间在知乎上了解下线性代数是做什么的就好了,这里只涉及线性代数的基础认识应用。
假如当我们有三个自变量 和一个因变量
,且符合线性关系。那么就会有以下方程成立:
再假设我们有四组数据,那么有:
于是我们可以抽象以下,写成矩阵的形式:
再抽象:
其中
我们的目的是求解 ,也就是把方程
中的
解出来。直接解个方程就能得到我们想要的效果,太好了,马上开始:
如果这里不理解的话,我简单说一下,求逆运算必须是形如 的形式,也就是行和列要相等。为什么这样呢?我的理解是矩阵是对一个线性空间到另一个线性空间的映射,所以如果一个矩阵的秩小于行数,也就是里面有线性相关的向量,在对线性空间进行变换时,可能进行降维影响,也就是造成某个维度塌缩,这种影响是不可逆的,所以这种矩阵是没有逆矩阵进行恢复的。如果要从一个向量映射到另一个向量,还有从另一个向量映射回来的话,这个矩阵必须有逆矩阵也就是满秩的。还有个东西叫奇异矩阵,感兴趣的可以了解一下。
回到主线,直接求解方程吧。
# coding: utf-8
import numpy as np
X1 = np.asarray([2104, 1416, 1534, 852]).reshape(4, 1)
X2 = np.asarray([5, 3, 3, 2]).reshape(4, 1)
X3 = np.asarray([1, 2, 2, 1]).reshape(4, 1)
X = np.mat(np.column_stack((X1, X2, X3, np.ones(shape=(4, 1)))))
noise = np.random.normal(0, 0.1, X1.shape)
Y = np.mat(2.5 * X1 - X2 + 2 * X3 + 4 + noise)
YTwin = np.mat(2.5 * X1 - X2 + 2 * X3 + 4)
W = (X.T * X).I * X.T * Y
WTWin = (X.T * X).I * X.T * YTwin
print(W, "\n", WTWin)
# output:
# [[ 2.50043958]
# [-1.16868808]
# [ 1.79213736]
# [ 4.27637958]]
# [[ 2.5]
# [-1. ]
# [ 2. ]
# [ 4. ]]
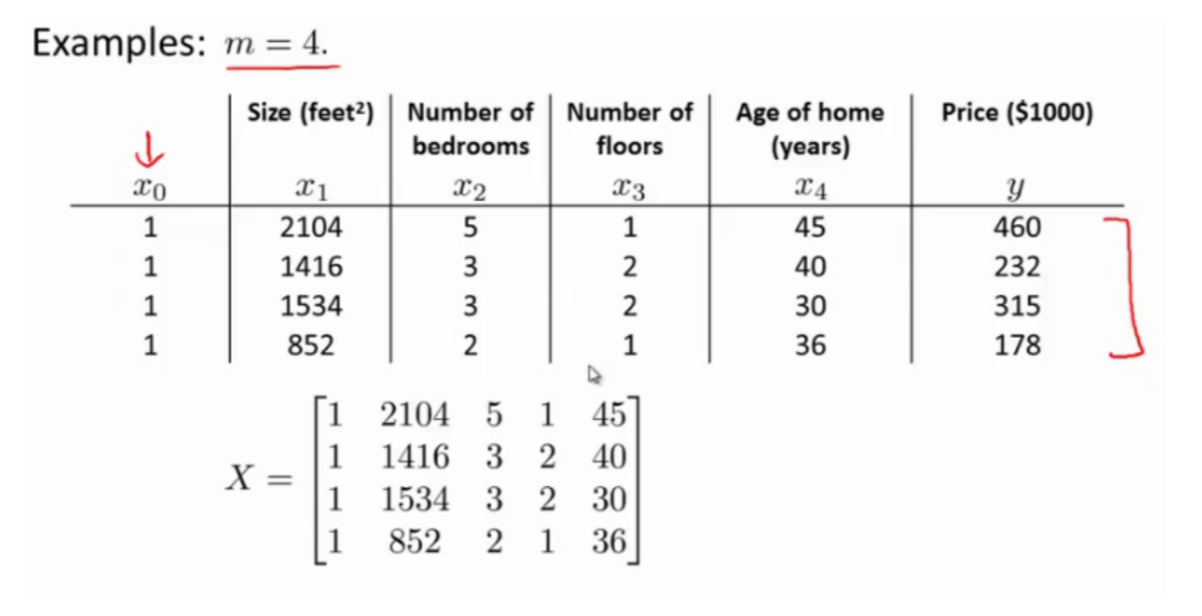
这里我们采用吴恩达老师的房子数据,自己生成的数据之间有太大的相似性,算出的结果误差太大。
我们基本可以计算多元线性回归,但是一点也体现不出机器学习中学习这个词,当然我们可以自己利用前面给出的例子利用 函数求解。这里我们借助
帮我们完成。
# coding: utf-8
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
N = 1000
train_X1 = np.linspace(1, 10, N).reshape(N, 1)
train_X2 = np.linspace(1, 10, N).reshape(N, 1)
train_X3 = np.linspace(1, 10, N).reshape(N, 1)
train_X4 = np.linspace(1, 10, N).reshape(N, 1)
# train_X = np.column_stack((train_X1, np.ones(shape=(N, 1))))
train_X = np.column_stack((train_X1, train_X2, train_X3, train_X4, np.ones(shape=(N, 1))))
noise = np.random.normal(0, 0.5, train_X1.shape)
# train_Y = 3 * train_X1 + 4
train_Y = train_X1 + train_X2 + train_X3 + train_X4 + 4 + noise
length = len(train_X[0])
X = tf.placeholder(tf.float32, [None, length], name="X")
Y = tf.placeholder(tf.float32, [None, 1], name="Y")
W = tf.Variable(np.random.random(size=length).reshape(length, 1), dtype=tf.float32, name="weight")
activation = tf.matmul(X, W)
learning_rate = 0.006
loss = tf.reduce_mean(tf.reduce_sum(tf.pow(activation - Y, 2), reduction_indices=[1]))
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
training_epochs = 2000
display_step = 100
loss_trace = []
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for epoch in range(training_epochs):
sess.run(optimizer, feed_dict={X: train_X, Y: train_Y})
temp_loss = sess.run(loss, feed_dict={X: train_X, Y: train_Y})
loss_trace.append(temp_loss)
if 1 == epoch % display_step:
print('epoch: %4s'%epoch, '\tloss: %s'%temp_loss)
print("\nOptimization Finished!")
print("\nloss = ", loss_trace[-1], "\nWeight =\n", sess.run(W, feed_dict={X: train_X, Y: train_Y}))
plt.plot(np.linspace(0, 100, 100), loss_trace[:100])
plt.savefig("tensorflowLR.png")
plt.show()
# output:
# epoch: 1 loss: 118.413925
# epoch: 101 loss: 1.4500043
# epoch: 201 loss: 1.0270562
# epoch: 301 loss: 0.75373846
# epoch: 401 loss: 0.5771168
# epoch: 501 loss: 0.46298113
# epoch: 601 loss: 0.38922414
# epoch: 701 loss: 0.34156123
# epoch: 801 loss: 0.31076077
# epoch: 901 loss: 0.29085675
# epoch: 1001 loss: 0.27799463
# epoch: 1101 loss: 0.26968285
# epoch: 1201 loss: 0.2643118
# epoch: 1301 loss: 0.26084095
# epoch: 1401 loss: 0.2585978
# epoch: 1501 loss: 0.25714833
# epoch: 1601 loss: 0.25621164
# epoch: 1701 loss: 0.2556064
# epoch: 1801 loss: 0.2552152
# epoch: 1901 loss: 0.2549625
# Optimization Finished!
# loss = 0.25480175
# Weight =
# [[1.0982682 ]
# [0.9760315 ]
# [1.0619627 ]
# [0.87049955]
# [3.9700394 ]]
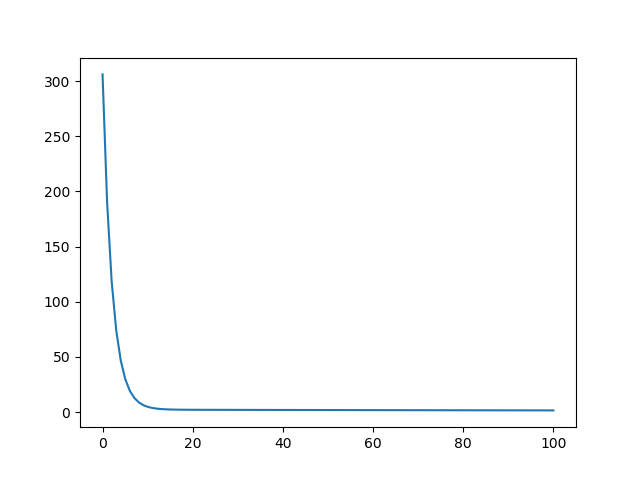
这里的拟合效果不太好,不知道是不是数据的问题,因为数据增长的相似性太高,感觉可能过拟合了,如果有知道的小伙伴欢迎告知。下图可以看到 早早就收敛了。
4 总结
线性回归的求解过程很直观,符合我们的理解。对于这个问题有一个先入为主的观点就是数据一定是拟合成线性的,因为这里讲的是线性回归。当然,数据分布不是线性的这个方法就不适用了,同样,如果我们看不到数据的分布,不能对模型进行预估,那只能一步一步去试探,所以机器学习开始就是选取适用于当前数据的模型,可以理解为找一个输入输出的合理映射关系,然后导入数据,构造一个能够正确评估拟合效果的损失函数,接着就是对损失函数进行最优化,这里有一个问题前面没有提及的是如果只是随机地找,其实我们不能保证找到的就是全局最优,当然一般情况下,局部最优得到的模型已经能很好的预测输出了。这只是我的个人理解啦,欢迎大家一起讨论,然后实验的代码在我的 GitHub 上,需要的可以自取。然后这个系列可能会继续更新,不过离下一次更新可能要点时间,因为新年快乐^_^,对了参考资料前面又给出,就不一一列举感谢了。