讲个故事
从身边的好朋友那里听说一个做程序的大哥,主要就是写算法的,然后从上家公司离职的时候,公司要求签订保密协议,并保证如果没有泄密的情况下,每月依然会发工资,持续两年
What?对,你没听错,就是这样,喵。为什么呢?因为他会算法啊,算法是根基,此处省略N多字,我也不会告诉你他年薪接近百万了。看到了吧,这就是我们要不断学习算法的小目标,先挣它一个亿!
算法的世界
Hi,欢迎来到算法的世界,算法无处不在,其实就在我们身边
- 《社交网络》中扎克伯格在创立Facebook之初靠着数学公式,写出了对比两个女孩照片谁更漂亮的算法
- 阿尔法狗打败了围棋世界冠军
- 进入X宝,会推荐你喜欢的商品
- 点个外卖,下次会推荐你常点的店家
- 打个农药,会尽量匹配和你选择英雄相同的玩家
- N多栗子,全举出来可能掘金都容不下这篇文章了
以上这些身边的例子其实都是依靠着算法来实现的
算法之于程序,是质变的过程(其实就是1分钟变1秒钟的差距)
程序 = 算法 + 数据结构
现在火热的AI技术,也并不是突然出现的,也是靠着之前积累的各种算法组合试验去运行的。
算法如同机器人的大脑,告诉机器人如何行动,思考等一系列行为。不然你以为,它们天生丽质难自弃嘛,那是不可能的
说了那么多,那我们为什么要学算法呢?为了挣它一个亿?可以是,也可以不是
没有一身好内功,招式再多都是空
对于我们大自然的搬运工(程序员)来说,算法可以让你的程序更加高效
好了,难道这还不够你臭屁的嘛!
下面开始今天的主题,先从简单的排序和搜索算法说起,因为很多中、高级面试里都会问到。连这些都答不上来还怎么当资深,做专家,挣它一个亿!
排序和搜索算法
排序算法
常用的排序算法有很多,如冒泡排序、选择排序、插入排序、归并排序、快速排序以及堆排序,下面我们就针对这几个排序算法来看看,了解一下思想
冒泡排序
// 创建一个数组列表来处理排序和搜索的数据结构
function ArrayList() {
let arr = [];
this.insert = function(item) { // 将数据插入到数组中
arr.push(item);
};
this.show = function() { // 展示数组的结构
return arr.join(' < ');
};
// 冒泡排序 眼熟?没错,面试里常考,而且它是排序算法中最简单的
this.bubbleSort = function () {
let len = arr.length;
for (let i = 0; i < len; i++) {
// 这里之所以再-i,是因为外层循环已经跑完一轮
// 内循环就没有必要再比较一回了
for (let j = 0; j < len - 1 - i; j++) {
if (arr[j] > arr[j + 1]) { // 当前项和下一项做比较,如果大于的话就按照下面交换位置
// ES6利用解构赋值的方式轻松实现j和j+1值的交换
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
}
}
}
};
}
// 测试用例,此测试用例在之后的算法中皆可使用
let arr = [5, 4, 3, 2, 1];
let createList = function(arr) {
let list = new ArrayList();
for (let i = 0; i < arr.length; i++) {
list.insert(arr[i]);
}
return list;
};
let item = createList(arr);
console.log(item.string()); // 排序前 5 < 4 < 3 < 2 < 1
item.bubbleSort();
console.log(item.string()); // 排序后 1 < 2 < 3 < 4 < 5
从实现方式来看冒泡排序是最简单的一种,而且从运行时间的角度来看,冒泡排序是最差的一个,因为做了两层循环导致,复杂度为O(n^2)了
下面再给大家看一下冒泡排序的工作流程:
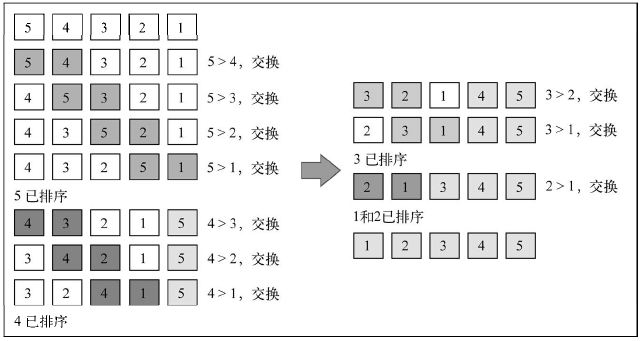
选择排序
所谓选择排序算法,其实就是拿数组中的一个值做标杆,和其他的值做比较,如果比标杆还小的就替换标杆的值,以此类推就可以了。不多啰嗦直接上代码
function ArrayList() {
// 省略...
// 选择排序
this.selectSort = function () {
let len = arr.length,
min;
for (let i = 0; i < len - 1; i++) {
min = i; // 我们取第一个值当标杆
for (let j = i; j < len; j++) { // 内部循环从i开始到数组结束
if (arr[min] > arr[j]) { // 比标杆的值还小,就替换新值
min = j;
}
}
if (i !== min) { // 上面经过一顿比较替换,如果标杆的值和之前取的第一个值不同了,就交换位置
[arr[i], arr[min]] = [arr[min], arr[i]];
}
}
};
}
选择排序我们看到其实也是嵌套了两层循环的操作,这样的话,其实复杂度和冒泡排序是一样的了,我们先来看下选择排序的工作流程吧
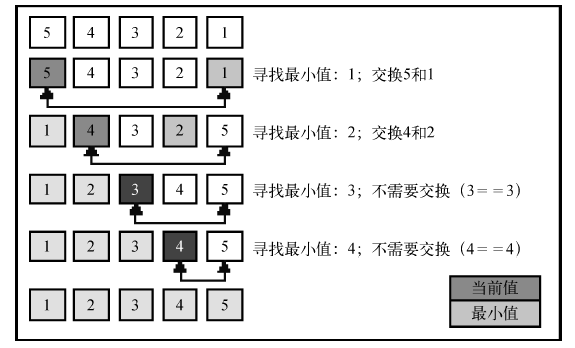
插入排序
插入排序算法是假定数组的第一项已经是排好序的了,直接用它和第二项去比较,如果比第二项大就将索引和值都进行交换,以此来推来实现排序
function ArrayList() {
// 省略...
// 插入排序
this.insertSort = function () {
let len = arr.length,
index, tmp;
// 这里默认第一项已经排序了,直接从第二项开始
for (let i = 1; i < len; i++) {
index = i; // 用来记录一个索引
tmp = arr[i]; // 储存一个临时变量,方便之后插入位置
// 索引必须是大于0,并且数组前一项的值如果大于临时变量的值
// 就将前一项的值赋给当期项,并且index--
while (index > 0 && arr[index - 1] > tmp) {
arr[index] = arr[index - 1];
index--;
}
arr[index] = tmp; // 最后在一顿替换后插入到了正确的位置上
}
};
}
// 测试用例写在冒泡排序那里
let arr = [3, 5, 1, 4, 2];
// 按照这个数组,先来分析前两项,剩下的大家自己来推到即可了
/*
Tips: -> 符号为最后对应的值
进入for循环i从1开始那此时
index = i -> 1; next -> 2
tmp = arr[1] -> 5; next -> arr[2] -> 1
while循环条件 1 > 0 && (arr[1-1]-> arr[0] -> 2) > 5
不成立继续循环
next 2>0 && 5 > 1
next 1>0 && 3 > 1
arr[2] = arr[1] -> 5
arr[1] = arr[0] -> 3
index--; index -> 1 index -> 0
最后
arr[index] = tmp -> arr[1] = 5; next arr[1] = 1 arr[0] = 1
就实现了值的交换
次时arr为[1, 3, 5, 4, 2]
剩下的以此类推即可了
*/
还是老样子,依然展示一下插入排序的工作流程:
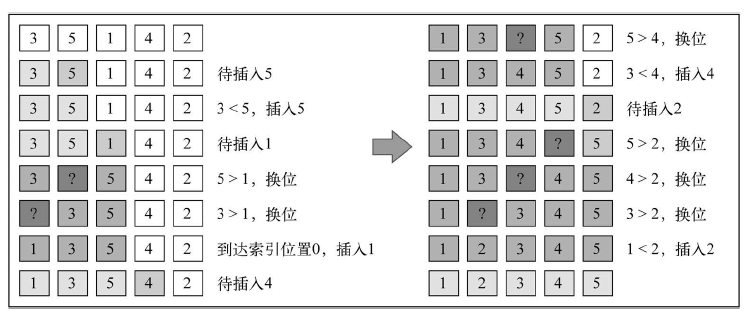
有时候想想同样是排序算法,怎么这三种算法是这也不行,那也不行。试问有没有靠谱的呢,大家时间宝贵不能耽误的。答案当然是肯定的,有,来看
归并排序
这里首先缅怀一位伟大的人物,冯·诺伊曼,‘计算机之父’。之所以要缅怀是因为这个靠谱的排序算法就是由这个开了挂的人提出的。恩,此时此景,我想吟诗一首,不简单啊,不简单!
function ArrayList() {
// 省略...
// 归并排序
this.mergeSort = function () {
arr = mergeRecurve(arr); // 由于需要不停的拆分直到数组只有一项,所以使用递归来做
};
// 递归
function mergeRecurve(arr) {
let len = arr.length;
// 递归的停止条件,如果数组只有一项,就直接返回了
// 这也是我们递归的目的,直到数组只有一项
if (len === 1) return arr;
let mid = Math.floor(len / 2);
let left = arr.slice(0, mid);
let right = arr.slice(mid, len); // 到这里把数组一分为二
// 为了不断对原数组拆分,对left和right数组继续递归,并作为参数传给merge函数
// merge函数负责合并和排序小数组为大数组
return merge(mergeRecurve(left), mergeRecurve(right));
}
function merge(left, right) { // 接收两个数组,最后合并到一起返回一个大数组
let res = [],
lLen = left.length,
rLen = right.length,
l = 0,
r = 0;
while (l < lLen && r < rLen) {
// 如果left数组的项比right数组的项小的话,就将left这里小的项添加到大数组里
if (left[l] < right[r]) {
res.push(left[l++]); // 并继续下一项比较
} else {
res.push(right[r++]); // 否则将right里小的项先添加到大数组中
}
}
// 将left和right数组中剩余的项也都添加到大数组中
while (l < lLen) {
res.push(left[l++]);
}
while (r < rLen) {
res.push(right[r++]);
}
return res; // 返回排好序的大数组
}
}
归并排序采用的是一种分治算法,不明白分治算法?很简单,你就当做是二分法。之后会讲,就是将一个大问题拆成小问题来解决,等每个小问题都解决了,大问题也就搞定了
实现思想:将原数组切分成小数组,直到每个数组只有一项,然后再将小数组合并成大数组,最后得到一个排好序的大数组。可以看下图的执行过程加深理解
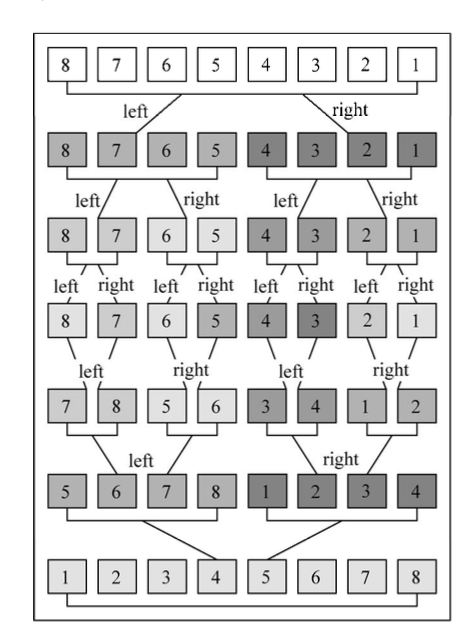
let arr = [7, 9, 8]; // 就选3个值的数组来简单分析吧
/*
arr = mergeRecurve([7, 9, 8])
二分拆分后,left = [7], right = [9, 8]
merge(mergeRecurve([7]), mergeRecurve([9, 8]))
[7]这个已经拆分完毕,先放着不管
由于数组并不是只有一项,所以[9, 8]继续递归
拆分后得到,left = [9], right = [8]
merge([9], [8])
res = [], l = 0, r = 0
while (0<1 && 0<1) {
if (9 < 8) {
不走这里
} else {
res.push(8)
}
}
while (0<1) {
res.push(9);
}
while(1<1) {
不走这里
}
return [8, 9]
再回到上一层处理merge([7], [8, 9]),推到过程同上
*/
少年,看到这里,我不得不说你果然骨骼惊奇,接下来放个大招,来介绍一下最常用的排序算法-快速排序,它的性能要比其他复杂度为O(nlog^n)的排序算法都好
快速排序
快速排序算法,需要在数组中找到一个中间项作为标记,然后创建双指针,左边第一项,右边最后一项。移动左指针直到比标记的值大,再移动右指针直到比标记小,然后交换位置,重复此过程,实现一个划分的操作
function ArrayList() {
// 省略...
// 快速排序
this.quickSort = function () {
quick(arr, 0, arr.length - 1); // 递归
}
function quick(arr, left, right) {
let index;
if (arr.length > 1) {
index = partition(arr, left, right); // 划分
if (left < index - 1) {
quick(arr, left, index - 1)
}
if (index < right) {
quick(arr, index, right);
}
}
}
// 划分函数
function partition(arr, left, right) {
let point = arr[Math.floor((left+right)/2)],
i = left,
j = right; // 双指针
while (i <= j) {
while (arr[i] < point) {
i++;
}
while (arr[j] > point) {
j--;
}
if (i<=j) {
[arr[i], arr[j]] = [arr[j], arr[i]]; // 交换位置
i++;
j--;
}
}
return i;
}
}
直接看代码可能有点懵,but不用怕,看见蟑螂也不怕不怕了。我们来具体问题具体分析一下就好了,直接看个简单的栗子
/*
let arr = [7, 9, 8];
quickSort
// 递归
quick([7, 9, 8], 0, 2) // 传递开头和末尾,两个位置
index // 用来分离小值数组和大值数组,一左一右
length > 1
对子数组进行划分,第一次传入的是原数组[7, 9, 8]
partition(arr, left, right) 用来划分位置
point = [7, 9, 8][Math.floor(0+2)/2] -> 9
i -> 0, j -> 2
// i 和 j 其实就是双指针,一个从左开始,一个从右开始
while (i <= j) { 0 <= 2
// 第一次 7 < 9
// 下一次 arr[1] -> 9 9 < 9不成立
while (arr[i] < 9) {
i++; i -> 1
}
// arr[2] -> 8 > 9不成立
while (arr[j] > 9) {
j--;
}
// 此时i->1, j->2
if (i <= j) { 1 <= 2
// 交换位置
[arr[i], arr[j]] = [arr[2], arr[1]] -> [8, 9]
i++; i -> 2
j--;
}
// 划分重排后的数组为[7, 8, 9]
return i; 返回划分的坐标i -> 2
}
此时计算出了index为2
if (left < index - 1) { 0 < 2-1
// 继续递归
quick([7, 8, 9], 0, 1);
// 这步递归完后,index->1,right->-1
}
if (index < right) {
quick([7,8,9], 2, 3);
}
按照以上步骤继续推到即可理解了,加油加油
*/
此时此刻,是不是该来一杯香浓的咖啡来提提神了呢?没有吗?没关系,那就抬起自己的右手慢慢向上抬起,高过头顶,然后......使劲拍一下脑袋,这下大家满足了吧,神清气爽,畅快淋漓了!哈哈,不扯淡了,不扯淡了
上面我们就聊了一下排序算法的几种不同方式,可以说是实现了初步胜利吧,算法的路还很长,路漫漫其修远兮,吾将上下而求索。大家一起共勉,下面再来聊聊搜索算法
请看大屏幕
搜索算法
搜索算法这里着重讲的就是面试中常被问到的二分查找法
我们大家都有用过array.indexOf方法,它的用法和字符串里的indexOf是一样的,都是返回所需元素的位置,没找到就是-1
说白了,这其实也算做一种搜索,只不过它的实现其实很low,不够高效,来看代码
let arr = [1, 9, 8, 2, 3];
arr.indexOf(8); // 2
arr.indexOf(0); // -1
function ArrayList() {
// 省略...
// indexOf
this.indexOf = function(item) {
for (let i = 0; i < arr.length; i++) {
if (item === arr[i]) {
return i;
}
}
return -1;
};
}
这样的代码实际上是按照顺序一个一个去做对比的,效率上有些低下。还是来看看我们的重点保护对象,二分查找法吧
二分查找法
看过早期李咏的《幸运52》的观众应该记得一个环节,节目会给嘉宾上一款商品,让他在一定时间内来猜价格,根据报价,李咏会说高了或者低了,直至回答正确拿到商品为止
没看过的朋友们,没关系,就是个猜价格的游戏,会说高了还是低了or对了
怀念当时还是个小盆友,无忧无虑的小盆友,哈哈
看代码
function ArrayList() {
// 省略...
// 二分查找法
this.binarySearch = function (item) {
this.quickSort(); // 先来排个序,方便查找
let low = 0,
high = arr.length - 1,
mid, ele;
while (low <= high) {
mid = Math.floor((low + high) / 2); // 一刀切,取中间
ele = arr[mid]; // 用中间值去和搜索值item比较
if (ele < item) { // 如果中间值是4,要查的是5
// 那就将左侧low的指针升级变成从中间加1项那里查找
// 就是在高价位那里查
low = mid + 1;
} else if (ele > item) { // 中间值还是4,要查的变成3了
// 比中间值还小,那就在靠左侧低价位里面了
// 将右侧指针变成中间值-1的位置,控制了最大范围
high = mid - 1;
} else { // 中间值是4,你查的正好也是4,那么,bingo,返回
return mid;
}
}
return -1; // 查不到的当然就-1了,这还用说嘛
};
}
二分查找法也聊完了,节目不早,时间刚好了。让我们一起来梳理一下上面的内容吧
梳理一下
排序算法
- 冒泡排序 -> 嵌套两层循环,和下面的选择排序一样性能不好
- 选择排序 -> 楼上的没脑子
- 插入排序 -> 相比楼上两位,它的性能会好很多,不过只适用于数据量少的数组
- 归并排序 -> 很有来头,被认可的排序算法
- 快速排序 -> 很常用的排序算法,性能也很好
搜索算法
- 二分查找法 -> 猜猜猜,押大押小,小了就在小的一侧找,大了就去大的一侧找
好了,以上内容在面试中、高级前端的时候也会被问到,在这里也希望看过此文章的同学,面试顺利,找到满意的工作
算法很有用,提高工作效率,重构的时候也很有效果
所以之后我也会继续研究学习算法的内容,好继续和大家分享,感谢各位了,骚年们!