数据结构笔记——二叉树的定义和性质

获取更多精彩内容，您还可以关注我的微信公众号——Android机动车。

在一些电视节目中，会猜测商品价格，有的人是一点一点的数字累加，这样的策略效率太低了。其实有一种经典的折半查找算法，就类似于我们今天要说的二叉树。

二叉树定义

二叉树：是n（n>=0）个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。

如下图就是一个二叉树：

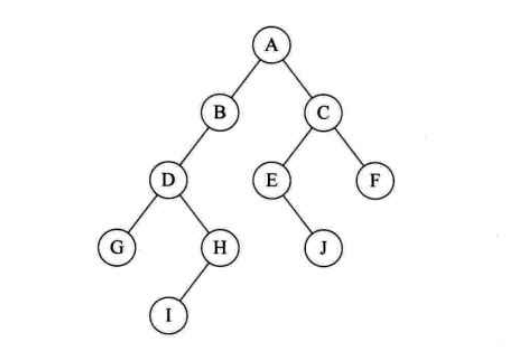
二叉树特点

二叉树的特点有：

每个结点最多两个子树，所以二叉树中不存在度大于2的结点。注意不是只有两棵子树，而是最多有。没有子树或者有一棵子树都是可以的。
左子树和右子树是有顺序的，次序布恩那个任意颠倒。
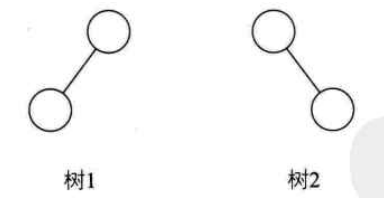
即使树中的某结点只有一棵子树，也要区分它是左子树还是右子树。如图：树1和树2是同一棵树，但却是不同的二叉树。

二叉树具有五种基本形态：

空二叉树；
只有一个根结点；
根结点只有左子树；
根结点只有右子树；
根结点既有左子树又有右子树。

特殊二叉树

再来介绍一些特殊的二叉树。

1、斜树

顾名思义，斜树一定是斜的，但是往那边斜还是有讲究的。

所有的结点都只有左子树的二叉树叫左斜树，所有结点都是只有右子树的二叉树叫右斜树。两种统称为斜树。

下面两个图分别就是左斜树和右斜树：

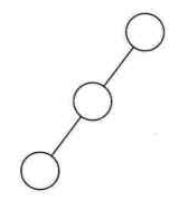
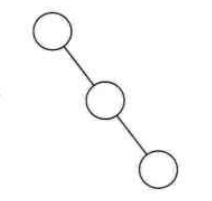
2、满二叉树

苏东坡有诗云：人有悲欢离合，月有阴晴圆缺，此事古难全。意思就是完美是理想，不完美才是人生。

我们通常看到的例子全是左高右低、参差不齐的二叉树，是否有完美的二叉树呢。

在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有的叶子结点都在同一层上，这样的二叉树叫做满二叉树。如图

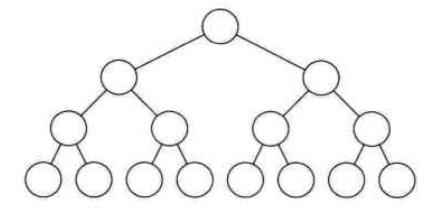
单单是每个结点都有左右子树，不能算是满二叉树，还必须要所有的叶子结点都处在同一层，这样就做到了二叉树的平衡。因此满二叉树的特点有：

叶子只能出现在最下面一层，出现在其他层就不能达到平衡；
非叶子结点的度一定是2；
同样深度的二叉树中，满二叉树的结点个数最多，叶子树最多。

3、完全二叉树

**对一棵具有n个结点的二叉树按层序编号，如果编号为i（1<=i<=n）的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。**如图：

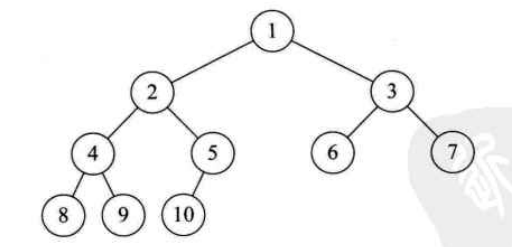
首先要从字面上区分，“完全”和“满”的差异，满二叉树一定是完全二叉树，完全二叉树不一定是满的。

注意完全二叉树中的编号与满二叉树中的相同，而且编号全部连续，有断开的就不是完全二叉树，如下图中的三棵树都不是完全二叉树。

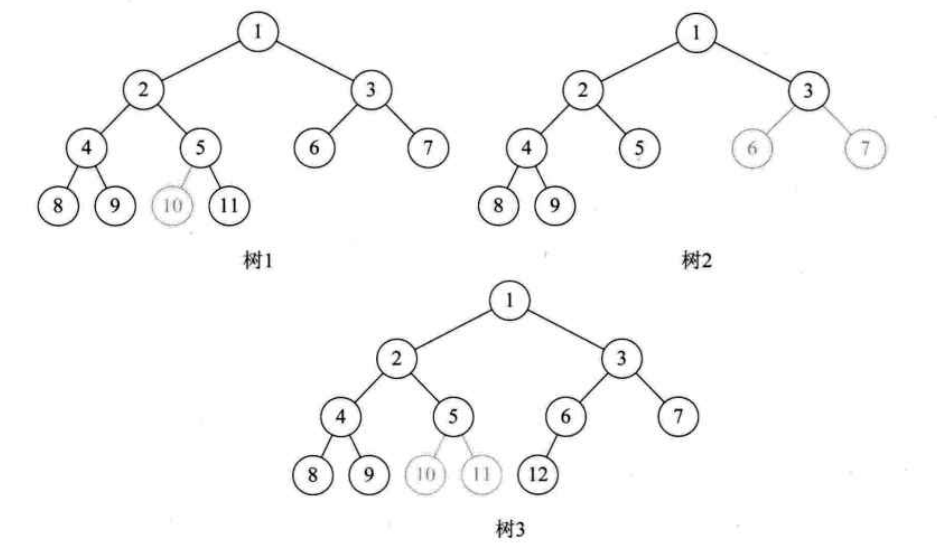
完全二叉树的特点：

叶子结点只能出现在最下面两层；
最下层的叶子一定集中在左部连续位置；
倒数二层，若有叶子结点，一定都在右部连续位置；
如果结点的度为1，则该结点只有左孩子，即不存在只有右子树的情况；
同样结点数的二叉树，完全二叉树深度最小。

我们也得出一个判断某二叉树是否是完全二叉树的方法，那就是看着树的示意图，心中默默给每个结点按照满二叉树的结构逐层顺序编号，如果编号出现空挡，就说明不是完全二叉树，否则就是。

二叉树的性质

二叉树有一些需要理解并记住的特性，便于更好地使用它。

二叉树性质1

在二叉树的第i层上至多有2^i-1个结点（i>=1）。

上图中：第1层： 1个： 2^1-1=2⁰=1 第2层： 1个： 2^2-1=2¹=2 第3层： 1个： 2^3-1=2²=4 第4层： 8个： 2^4-1=2³=8

通过数据归纳法，很容易得出在二叉树的第i层上最多有 2^i-1个结点。

二叉树性质2

深度为k的二叉树最多有2^k-1个结点（k>=1）。

这里注意是2的k次幂再减1。

如果有一层，最多1=2¹-1个结点如果有两层，最多1+2=2²-1个结点如果有三层，最多1+2+4=2³-1个结点如果有四层，最多1+2+4+8=2⁴-1个结点

通过数据归纳法的论证，可以得出如果有k层，结点数最多为2^k-1。

二叉树性质3

对任何一棵二叉树T，如果其终端结点数为n₀，度为2的结点数为n₂，则n₀=n₂+1。

终端结点就是叶子结点，而一棵二叉树，除了叶子结点外，剩下的就是度为1和2的结点了，设n₁是度为1的结点数。则树T的结点总数就是n=n₀+n₁+n₂。

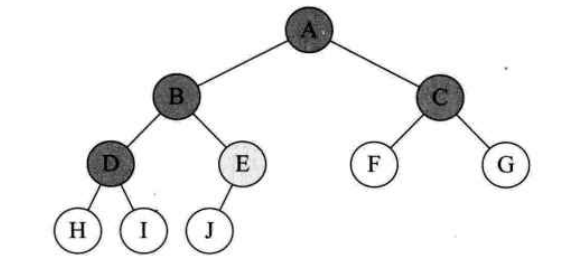
我们换个角度，再数一数连接线，由于根结点只有分支出去，没有分支进入，所以分支线总数为结点总数减去1，n-1=n₁+2n₂，又因为n=n₀+n₁+n₂，得出n₀=n₂+1 。

二叉树性质4

具有n个结点的完全二叉树的深度为不大于log₂n的最大整数+1 。

这里不再详细推导。

二叉树性质5

如果对一棵有n个结点的完全二叉树的结点按层序编号（从第一层到最后一层，每层从左到右），对任一结点i（1<=i<=n）有：

如果i=1，则结点i是二叉树的根，无双亲；如果i>1，则其双亲是结点 ⌊ i/2 ⌋ 。
如果2i>n，则结点i无左孩子（结点i为叶子结点）；否则其左孩子是结点2i 。
如果2i+1>n，则结点i无右孩子；否则其右孩子是结点2i+1 。

下篇文章会讲到二叉树的存储结构和遍历二叉树，希望大家持续关注。

更多精彩内容，欢迎关注我的微信公众号——Android机动车。