伯克利提出时序差分模型TDM：让深度强化学习更像人类

你决定骑自行车从加州大学伯克利分校的住处到金门大桥。这是一段 20 英里的美妙旅程，但是有个问题：你从来没有骑过自行车！更糟糕的是，你是湾区的新人，而你只有一张地图，那要如何开始呢？

让我们先搞清楚大家都是如何学会骑自行车的。

有一种策略是进行大量的学习和规划：阅读如何骑自行车的书籍、研究物理学和解剖学。计划出你为了应对每个扰动做出的所有肌肉运动。这种方法看起来高大上，但是对于任何学过骑自行车的人来说，都知道这种策略注定要失败。学骑自行车的方法只有一种：试错。有些任务，像骑自行车这样的任务，真的太复杂了，以至于根本无法在脑子里预先计划好。

AI 前线注：试错（trial and error）是一种用来解决问题、获取知识的常见方法。此种方法可视为简易解决问题的方法中的一种，与使用洞察力和理论推导的方法正好相反。在试错的过程中，选择一个可能的解法应用在待解问题上，经过验证后如果失败，选择另一个可能的解法再接着尝试下去。整个过程在其中一个尝试解法产生出正确结果时结束。

一旦你学会了骑自行车，你将如何到达金门大桥呢？你可以重复使用试错策略。随便转几圈，看看你是否在金门大桥上。但不幸的是，这种策略需要耗费很长的时间。对于这类问题，计划是一个更快的策略，并且只需相当少的实际经验及更少的试错。用强化学习的术语来讲，它更具有样本效率（sample-efficient）。

左：一些可通过试错学到的技能。右：其他时候，提前计划比较好。

虽然简单，但这个思维实验突出了人类智能的一些重要方面。对于某些任务，我们采用试错法；而对于其他任务我们则使用规划的方法。在强化学习中也出现了类似的现象。按照强化学习的说法，实证结果表明，一些任务更适合无模型（试错）方法，而另一些则更适合基于模型的（规划）方法。

上面这个骑自行车的比喻，也强调这两个系统并非完全独立。特别是，说学骑自行车只是试错法的过分简单化。事实上，当你通过试错法来学骑车的时候，你也会运用一些计划。也许你最初的计划是“不要跌倒”。随着你的进步，你就会做出更加雄心勃勃的计划，如“往前骑两米而不会跌倒”。最终，你骑车技巧炉火纯青，这时你可以开始以非常抽象的方式进行规划（如“骑车到这条路的尽头。”），剩下所有的事就是规划，而无须再担心骑车的细节了。我们目睹了从无模型（试错）策略逐步过渡到基于模型的（规划）策略。如果我们可以开发出人工智能算法（特别是强化学习算法）来模拟这种行为，它可能会产生一种这样的算法：既能很好地执行（通过在早期使用试错法），并且能够提高样本效率。（稍后切换到规划方法来实现更为抽象的目标）。

本文介绍了时序差分模型（temporal difference model，TDM），这是强化学习算法的一种，它可以捕获无模型和基于模型的强化学习之间的平滑过渡。在讲述 TDM 之前，我们首先阐述典型的基于模型的强化学习算法是如何工作的。

AI 前线注：时序差分学习（Temporal-Difference Learning）结合了动态规划和蒙特卡洛方法，是强化学习的核心思想。蒙特卡洛的方法是模拟（或者经历）一段序列，在序列结束后，根据序列上各个状态的价值，来估计状态价值。时序差分学习是模拟（或者经历）一段序列，每行动一步（或者几步），根据新状态的价值，然后估计执行前的状态价值。可以认为蒙特卡洛的方法是最大步数的时序差分学习。

在强化学习中，我们有一些状态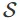空间和动作空间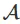。如果在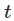时刻我们处于状态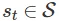采取行动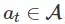，我们根据动态模型 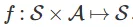过渡到一个新的状态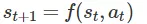。我们的目标是最大化访问状态的奖励总和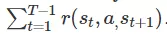。基于模型的强化学习算法假定给出（或学习）动态模型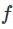。给定这个动态模型，有多种基于模型的算法。对于本文而言，我们考虑执行以下优化的方法来选择一系列操作和状态以最大化奖励：

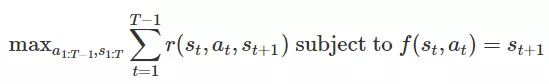
优化方法建议选择一系列状态和行动，即可最大化奖励，同时确保轨迹是可行的。

在这里，可行的意思是每一种状态下的状态转换都是有效的。例如，如下图所示，如果你从状态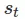 开始并采取行动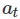，则只有最上面的 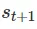才能实现一个可行的转换。

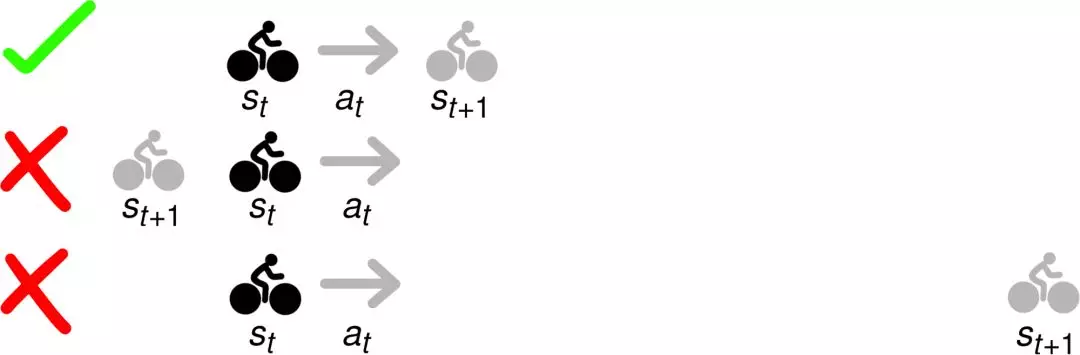
如果你能挑战物理学的话，那么去金门大桥的旅行计划就会容易得多。但是，基于模型的优化问题中的约束确保只有像第一行这样的轨迹才能被输出。底部的两条轨迹可能有很高的回报，但它们并不可行。

在我们的自行车问题中，优化可能会制定从伯克利（图右上）到金门大桥（图左中）的骑行计划，看起来如下图所示：

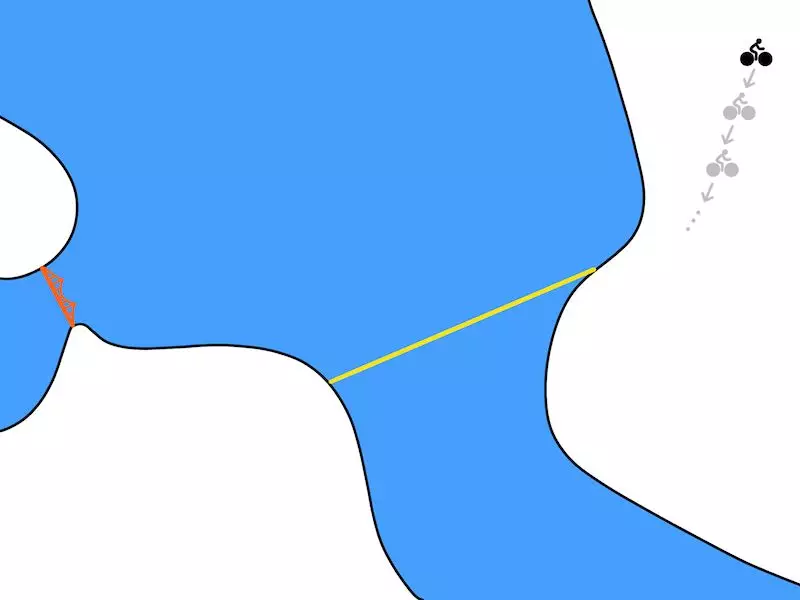
一个计划（状态和行动）的示例输出了优化问题。

虽然从理论概念来看还不错，但是这个计划不太现实。基于模型的方法使用一个模型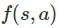来预测下一个时间步的状态，在机器人技术中，时间步通常相当于十分之一秒或百分之一秒。因此，对最终计划可能会有一个更现实的描述，如下图所示：

一个更现实的计划。

如果我们想想在日常生活中的计划，就会意识到我们的计划在时序上更为抽象。我们不会去预测自行车在接下来的十分之一秒将处于什么位置，而是制定了更为长远的计划，比如“我将走到这条路的尽头”。此外，一旦我们学会了如何骑车，我们就只能做出这些时序抽象规划。如前所述，我们需要一些方法：（1）使用试错法来是学习，（2）提供一种机制来逐步提高我们用于计划的抽象级别。为此，我们引入了时序差分模型。

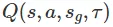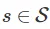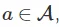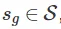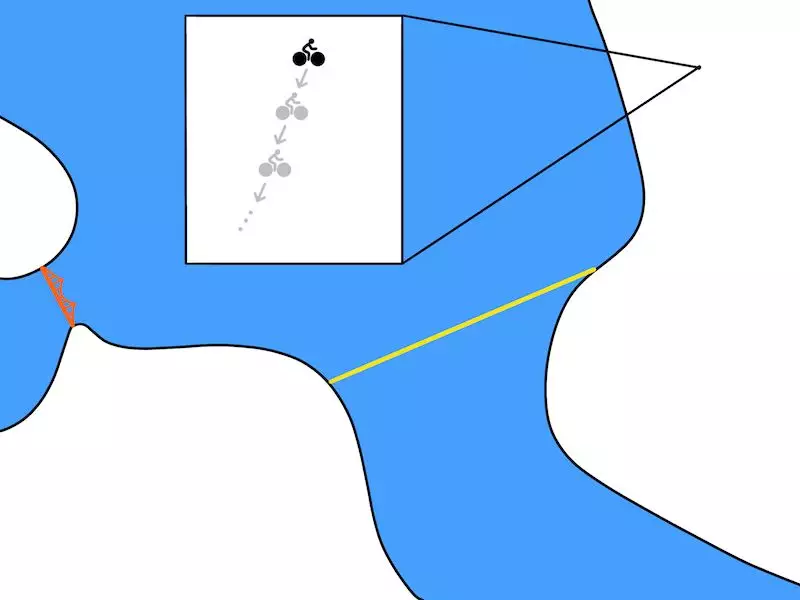
一个时序差分模型 (TDM)，我们将它写成，它是一个函数，给定一个状态，动作，和目标状态，预测智能体在时间步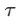 内达到目标的程度。直观地说，TDM 回答了这样的问题:“如果我在 30 分钟内骑车到旧金山，我将会有多接近?”对于机器人技术来说，一种测量贴近度的自然方法是使用欧氏距离（Euclidean distance）。

AI 前线注：欧氏距离，亦称为欧几里得距离，在数据上，是欧几里得空间中两点间“普通”（即直线）距离。使用这个距离，欧氏空间成为度量空间。相关联的范数称为欧几里得范数。较早的文献称之为毕达哥拉斯度量。

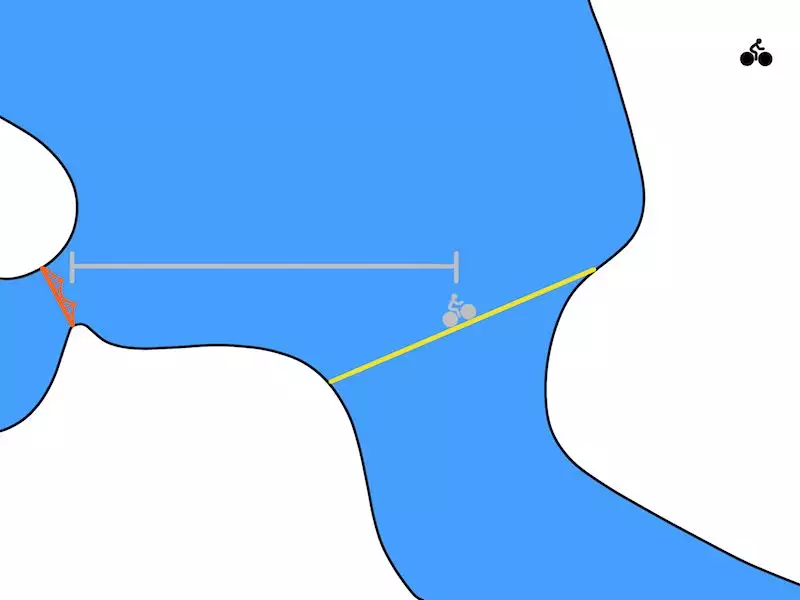
TDM 预测在一段固定的时间之后，你距离目标（金门大桥）有多近。骑车 30 分钟后，也许你只能到达上图中灰色骑行人的位置。在这种情况下，灰色线段表示 TDM 应该预测的距离。

对于那些熟悉强化学习的人来说，事实证明 TDM 可以被看作是有限视域 MDP 中的目标条件 Q 函数。因为 TDM 只是另一个 Q 函数，因此我们可以使用无模型（试错）算法对其进行训练。我们使用深度确定性策略梯度（deep deterministic policy gradient，DDPG）来训练 TDM，并对目标和时间层进行追溯，以提高学习算法的样本效率。理论上来讲，任何 Q 学习算法都可以用来训练 TDM，但我们发现这个是有效的，欢迎读者查阅相关论文了解更多的细节。

AI 前线注：深度确定性策略梯度（Deep Deterministic Policy Gradient， DDPG）算法是 Lillicrap 等人利用 DQN 扩展 Q 学习算法的思路对确定性策略梯度（Deterministic Policy Gradient， DPG）方法进行改造，提出的一种基于行动者 - 评论家（Actor-Critic，AC）框架的算法，该算法可用于解决连续动作空间上的 DRL 问题。

参见论文《Continuous control with deep reinforcement learning》

https://arxiv.org/abs/1509.02971

一旦我们训练 TDM，我们如何使用它来进行规划？事实证明，我们可以通过以下优化方法来规划：

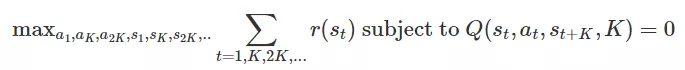
这种直觉与基于模型的公式类似。选择一连串的行动和状态来最大化回报是可行的。一个关键的区别是我们只计划每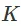 个时间步，而不是每个时间步。 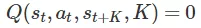的约束强制了轨迹的可行性。形象化地说， 而不是明确规划 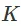步骤和类似的动作：

我们可以直接计划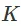 时间步，如下图所示：

随着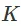 的增加，我们在时序上得到了越来越抽象的计划。在 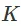个时间步骤之间，我们使用无模型的方法来采取行动，从而使无模型的策略“抽象”了实现目标的细节。对于自行车问题和 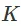的足够大的值，优化可能会制定如下计划：

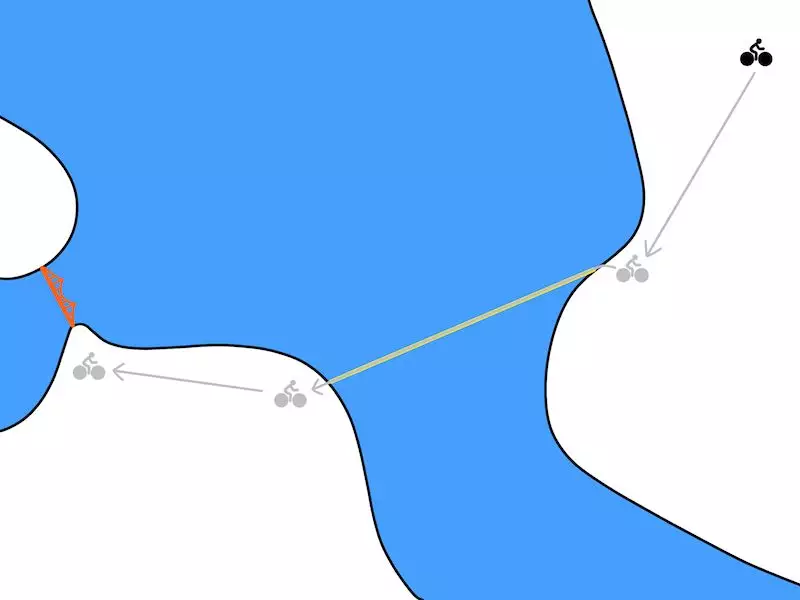
基于模型的计划者可以用来选择时序抽象的目标。可以使用无模型算法实现这些目标。

有一点需要注意的是，这个公式只能在每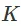 步骤中优化奖励。然而，许多任务只关心一些状态，比如最终状态 (例如“到达金门大桥”)，因此它仍然捕捉到各种有趣的任务。

我们并非第一个研究基于模型和无模型强化之间的联系的人。Parr'08[¹] 和 Boyan'99[²]，关联性尤其强，尽管它们主要集中在列表和线性函数的逼近器上。在 Sutton'11[³] 和 Schaul'15[⁴] 中，在机器人导航和 Atari 游戏中也探索了训练目标条件 Q 函数的想法。最后，我们所使用的重新标记方案受到 Andrychowicz 17[⁵] 的启发。

我们在五个模拟连续控制任务和一个真实世界中的机器人任务上测试了 TDM。其中一项模拟任务是训练机器人手臂将圆桶推到目标位置。下图显示了最终推动 TDM 策略的关联学习曲线的一个示例：

TDM 策略用于完成任务的演示动图无法上传，可访问：http://bair.berkeley.edu/static/blog/tdm/pusher-video-small.gif 。

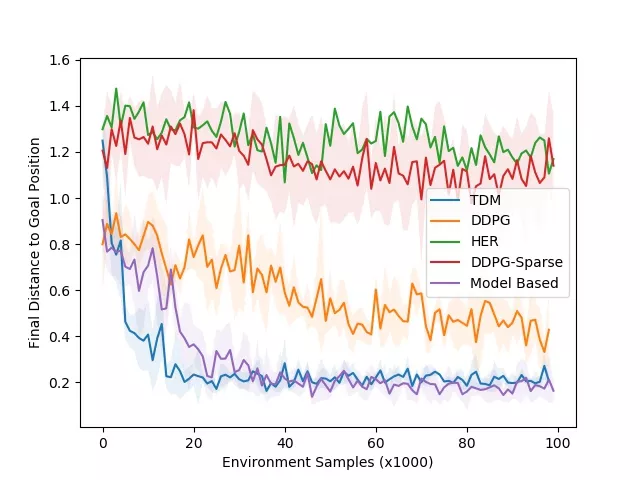
学习曲线。蓝线为 TDM（越低越好）。

上图所示的学习曲线展示了最终目标的距离与样本的数量直接的关系（越低越好）。我们的仿真以 20Hz 控制机器人，这表示 1000 步对应于现实世界的 50 秒。这种环境的动态相对容易学习，这意味着基于模型的方法应该很出色。正如预期那样，基于模型的方法（紫色曲线）快速学习——大约 3000 步，或 25 分钟——且表现良好。TDM 方法（蓝色曲线）也可以快速学习——大约 2000 步或 17 分钟。无模型的 DDPG（无 TDM）基线最终解决了这个任务，但需要更多的训练样本。TDM 方法能够如此快速学习的一个原因就是它的有效性是基于模型的伪装方法。

当我们转向运动任务时，无模型方法看起来好多了，而运动任务的动态性更强。其中一项运动任务涉及训练四足机器人移动到某个位置。由此产生的 TDM 策略将在下图显示，以及相应的学习曲线：

运动任务的 TDM 策略。

学习曲线。蓝线为 TDM（越低越好）。

就像我们使用试错法而不是计划掌握骑自行车一样，我们期望无模型的方法在这些运动任务上比基于模型的方法执行得更好。这正是我们在上图的学习曲线上看到的: 基于模型的方法在性能上保持平稳。无模型的 DDPG 方法学习更慢，但最终优于基于模型的方法。TDM 能够快速学习并获得最佳的最终性能。在这篇论文中还有更多的实验，包括训练一个真实世界 7 自由度的 Sawyer 来达到自己的位置。我们鼓励读者去看看!

时序差分模型为从无模型到基于模型的控制插值提供了一种形式化和实用的算法。但是未来还有很多工作要做。首先，推到假定环境和策略是确定性的。实际上，大多数环境是随机的。即使它们是确定性的，在实践中使用随机策略也有令人信服的理由（参见此博文《Learning Diverse Skills via Maximum Entropy Deep Reinforcement Learning》[⁶]）。将 TDM 拓展到此设置，有助于将 TDM 移至更真实的环境。另一个想法是，将 TDM 与基于模型的规划优化算法结合在一起，本文中，我们使用了这些算法。最后，我们希望将 TDM 应用到更具挑战性的任务中，比如机器人的运动、操纵，当然还有骑车到金门大桥。

本论文已经被 ICLR 2018 接收。欲了解更多关于 TDM 的信息，请查看以下链接：

• ArXiv Preprint https://arxiv.org/abs/1802.09081

• 开源代码 https://github.com/vitchyr/rlkit

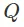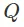我们称之为时序差分模型，因为我们用时序差分学习训练 并使用 作为模型。

参考资料：

[1] https://users.cs.duke.edu/~parr/icml08.pdf

[2] https://pdfs.semanticscholar.org/61d4/897dbf7ced83a0eb830a8de0dd64abb58ebd.pdf

[3] http://www.incompleteideas.net/papers/horde-aamas-11.pdf

[4] http://proceedings.mlr.press/v37/schaul15.pdf

[5] https://arxiv.org/abs/1707.01495

[6] http://bair.berkeley.edu/blog/2017/10/06/soft-q-learning/

原文链接：

TDM: From Model-Free to Model-Based Deep Reinforcement Learning

http://bair.berkeley.edu/blog/2018/04/26/tdm/