相关文章目录:
- 机器学习 之线性回归
- 机器学习 之逻辑回归及python实现
- 机器学习项目实战 交易数据异常检测
- 机器学习之 决策树(Decision Tree)
- 机器学习之 决策树(Decision Tree)python实现
- 机器学习之 PCA(主成分分析)
- 机器学习之 特征工程
linear regreesion(线性回归)
我们将用来描述回归问题的标记如下:
代表训练集中实例的数量
代表特征的数量
表示第
个训练实例,是特征矩阵的第i行,是一个向量
表示特征矩阵中第
行的第
个特征,也就是第
个训练实例的第
个特征
代表目标变量,也就是输出变量
代表训练集中的一个实例
代表第
个观察实例
代表学习算法的函数,或者加假设(hypothesis)
对于多变量线性回归,假设函数可以设为
为了使公式能够简化,引入
则假设函数变为
进行向量化后,最终结果为
我们需要求出,使得对于每一个样本,带入到假设函数中,能得到对应的一个预测值,而我们的目标,是使求出的预测值尽可能的接近真实值
通过最大似然估计来推导目标函数
由于我们实际预测的值和真实值之间肯定会有误差,对于每个样本:
其中,为当前样本实际真实值,
为预测结果,
即为预测误差
对于整个数据集来说,则:
误差 是独立的并且具有相同的分布,并且服从均值为0,方差为
的正态分布
由于误差服从正态分布,所以:
带入得:
我们希望误差越接近0越好,由于误差服从均值为0的正态分布,所以对应误差越接近分布的中心处越好。我们可以近似的用对应概率来表示当前正态分布的纵坐标值,则由于各个样本的误差互相独立,所以,将每个样本误差概率相乘,得总似然函数为:
我们的问题是希望找到合适的,与我们的数据组合后尽可能的接近真实值
所以我们需要求解上述似然函数的针对于
最大值,即求解最大似然函数
由于上述似然函数中的累乘运算过于复杂,我们可以将其进行转换,变成对数似然,求加和,即:
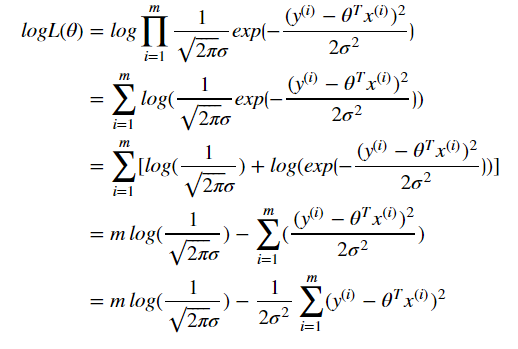
上述公式中, 都是已知的,只有
是未知的。
所以我们的目标是 找出一组
,使上述似然函数最大,即求最大似然函数。
由于只有
是未知的。上述问题可以转换为,求
的最小值
最终,得出我们的目标函数(也称为代价函数)为:
进行向量化:
正规方程
要求取得最小值时对应的
值,一个办法就是求偏导。由于
为凸函数,所以在偏导等于0处取得最小值,此时的
即为我们所需要的,并且也是最优解
这种直接令偏导等于0,解方程得出
的方法称为正规方程
令,得:
虽然,通过正规方程,可以求得最优解,但是,在实际项目中,我们的样本数量以及每个样本的特征 数量非常大,这个时候,采用正规方程,算法的时间复杂度太高,耗时太高,甚至由于样本呢和特征过大,或者矩阵不可逆,导致无法计算。 尤其对于矩阵求逆来说更是如此。所以,一般对于样本数量和特征数量较少时可以采用此种求解方式。
对于一般情况,我们需要采用另外一种非常经典的优化算法,即 梯度下降法
梯度下降法
对于直接求解正规方程的方式,首先,并不一定可解,另外,时间复杂度过高。 而机器学习的常规套路,都是使用梯度下降法,去求解最小值问题。
梯度下降背后的思想是:
开始时我们随机选择一组参数.计算对应代价函数,然后我们需要寻找下一组能让代价函数值下降最多的参数组合,一直迭代这个过程,直到最后代价函数值收敛,即找到一个局部最小值. 此时对应的
即为我们需要求的结果.
我们并没有尝试找出所有的参数组合,所以,不能确定我们得到的局部最小值是否是全局最小值。 但是,对于线性回归的代价函数来说,其实本身是个凸优化问题,所以局部最小值即为全局最小值!
换个思路来理解,比如,你现在站在山上某一点,你需要下山,到达山底(即需要找到最小值点)<br> 在梯度下降算法中,你要做的就是,环顾四周,找到一个方向,往下走一步,然后再重新查找方向,往下走一步,以此循环,直到到达山底。<br> 上述场景中,影响到达山底的因素有两个,一个是方向,另外一个是步长。<br> 要想能快速到底山底,我们首先需要保证每步走的都是最陡的方向,然后步子迈大点。 而最陡的方向,即为梯度,又因为是找最小值,所以得沿着负梯度的方向,这就是梯度下降法
下面,我们正式说下<br>
梯度下降法的基本结构(最小化) (下面表述中的
表示第几次迭代)<br>
- 选择一个初始点,即选择一组参数
- 选取搜索方向
,使得函数下降最快
- 决定步长
,使得
对于
最小化,构建
- 可以开始时设置一个阈值
,如果
,则停止迭代,输出解
,否则继续重复迭代。 当然我们也可以直接设置迭代次数。<br><br> 需要注意下,上述中的
指的是第k次迭代时的一组参数,即
下面说下,梯度下降中的三种方式,即:批量梯度下降,随机梯度下降和小批量梯度下降
批量梯度下降
批量梯度下降,其实就是在每次迭代中,在更新一组参数中的任意一个时,都需要对整个样本的代价函数
求对应梯度 <br>
他的优点是 容易得到最优解,但是由于每次都需要考虑所有样本,所以速度很慢
下面看下具体数学表示
对于某次迭代
其中,,即特征个数
进行向量化后,对于每次迭代
随机梯度下降
随机梯度下降,其实就是在每次迭代中,在更新一组参数中的任意一个时,只需要找一个样本求对应梯度,进行更新。
他的优点是 迭代速度快,但是不一定每次都朝着收敛的方向
具体数学表示为:
小批量梯度下降
小批量梯度下降,其实就是在每次迭代中,在更新一组参数中的任意一个时,找一部分样本求对应梯度,进行更新。
小批量梯度下降 其实就是上述两种方法的权衡,实际应用中,大部分也都用此算法
学习率(步长)
梯度下降法中有两个因素,一个是方向,即梯度,另外一个就是学习率,也就是步长。
如果学习率过小,则达到收敛(也就是近似接近于最小值)所需要的迭代次数会非常高。 学习率过大,则可能会越过局部最小值点,导致无法收敛
欢迎关注我的个人公众号 AI计算机视觉工坊,本公众号不定期推送机器学习,深度学习,计算机视觉等相关文章,欢迎大家和我一起学习,交流。
