逻辑回归(Logistic Regression)

首先需要说明，逻辑回归属于分类算法。分类问题和回归问题的区别在于，分类问题的输出是离散的，如（0，1，2，...）而回归问题的输出是连续的。

我们将要用来描述这个分类问题的标记如下:

$m$ 代表训练集中实例的数量

$n$ 代表特征的数量

$x^{(i)}$ 表示第 $i$ 个训练实例，是特征矩阵的第i行，是一个向量

$x_j^{(i)}$ 表示特征矩阵中第 $i$ 行的第 $j$ 个特征，也就是第 $i$ 个训练实例的第 $j$ 个特征

$y$ 代表目标变量，也就是输出变量

$(x,y)$ 代表训练集中的一个实例

$(x^{(i)},y^{(i)})$ 代表第 $i$ 个观察实例

$h$ 代表学习算法的函数，或者假设（hypothesis）

假设函数

逻辑回归是在线性回归的基础上，转化而来的。它是用来解决经典的二分类问题

首先说明下，什么是二分类问题

我们将输出结果 $y$ 可能属于的两个类分别称为负向类（negative class）和正向类（positive class），则输出结果 $y$ 属于0，1 ，其中 0 表示负向类，1 表示正向类。

我们将线性回归的输出记为：

我们知道，线性回归的输出结果是实数域中连续的，要想解决二分类问题，这时，我们引入Sigmoid函数，对应公式为：

对应图像如上图，可见，自变量取值为任意实数，值域为[0,1]

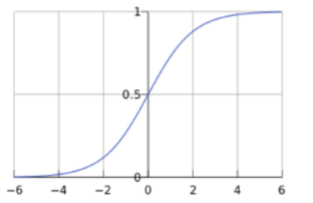
经过sigmoid函数，就将任意的输入映射到了[0,1]区间内，我们在线性回归中可以得到一个预测值，再将该值进映射到Sigmoid函数中，这样就完成了由值到概率的转换，这就是逻辑回归中的分类任务

所以，我们逻辑回归的假设函数为：

h_{\theta}(x) = g(\theta^TX) = \frac{1}{1+e^{-\theta^TX}}

逻辑回归的假设函数 $h_{\theta}(x)$ 即为对应y=1的概率值，即我们可以用下式表示：

一般情况下，我们判定当 $h_{\theta}(x) >=0.5$ 时，预测 $y=1$ ,当 $h_{\theta}(x) < 0.5$ 时，预测 $y=0$ 。

目标函数

将上述概率进行整合，我们得出：

P(y\,|\,x;\theta) = (h_{\theta}(x))^y(1-h_{\theta}(x))^{1-y}

其中， $y$ 属于 $0,1$ 由于每个样本最后得出的概率值都是独立的，所以，对于所有样本来说，我们可以得到对应似然函数为：

L(\theta) = \prod_{i=1}^{m} P(y^{(i)}\,|\,x^{(i)};\theta) =\prod_{i=1}^{m} (h_{\theta}(x^{(i)}))^{y^{(i)}}(1-h_{\theta}(x^{(i)}))^{1-y^{(i)}}

最终，我们的目标就是求解最大似然函数，也就是让所有样本数据最终求得是正向类或者负向类的概率越大越好。

为了计算方便，首先，我们对上述似然函数取对数，得

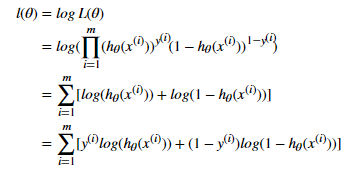
这个时候，我们是求的最大值，为了转换为梯度下降任务，所以我们引入 $J(\theta) = -\frac{1}{m}l(\theta)$

最终，我们的目标函数为：

J(\theta) = -\frac{1}{m}\sum_ {i=1}^{m} [y^{(i)}log(h_{\theta}(x^{(i)}))+(1-y^{(i)})log(1-h_{\theta}(x^{(i)}))]

gradient descent(梯度下降)

对代价函数求偏导，得：

\frac{\partial J(\theta)}{\partial \theta_j} = {\frac{1}{m}} \sum_ {i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}

向量化后，得：

\frac{\partial J(\theta)}{\partial \theta} = \frac{1}{m}X^T(Sigmoid(\theta X)-y)

决策边界

在逻辑回归中，我们预测：

当 $h_{\theta}(x) >=0.5$ 时，预测 $y=1$ ,当 $h_{\theta}(x) < 0.5$ 时，预测 $y=0$ 。

即：当 $\theta^TX >= 0$ 时，预测 $y=1$ ,当 $\theta^TX < 0$ 时，预测 $y=1$ 。

所以，决策边界为：

梯度下降求解逻辑回归问题

下面，通过逻辑回归模型，来实现一个预测某个学生是否会被大学录取的问题。假设你是一个大学系的管理员，你想根据两次考试的结果来决定每个申请人的录取机会，现在你拥有之前申请学生的可以用于训练逻辑回归的训练样本集。对于每一个训练样本，你有他们两次测试的评分和最后是被录取的结果。为了完成这个预测任务，我们准备构建一个可以基于两次测试评分来评估录取可能性的分类模型。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import classification_report#这个包是评价报告

首先，让我们获取下数据，看下数据结构

#exam1,exam2代表两次测试评分，也就是特征值x1,y1，admitted为录取结果，也就是y
data = pd.read_csv('ex2data1.txt',names=['exam1','exam2','admitted'])
data.head()  #打印前五行，看看

	exam1	exam2	admitted
0	34.623660	78.024693	0
1	30.286711	43.894998	0
2	35.847409	72.902198	0
3	60.182599	86.308552	1
4	79.032736	75.344376	1

通常情况下，进行相关数据可视化，可以帮我们更好的分析数据

# 数据可视化
sns.lmplot('exam1','exam2', hue='admitted', data=data, size=6,fit_reg=False,scatter_kws={"s":50})
plt.show()

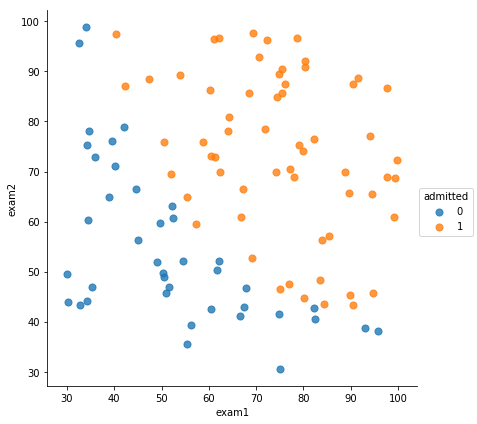
数据初始化

包括分离出特征值和输出变量，进行特征缩放以及theat向量的初始化等操作

#进行归一化处理，也就是特征缩放（注意，这块只是针对特征，也就是X）
def normalize_feature(df):
    data_explame = df.iloc[:,:-1]
    data_x = data_explame.apply(lambda column: (column - column.mean())/column.std())
    data = pd.concat([data_x,df.iloc[:,-1]], axis=1)
    return data

#插入x0列并转换为ndarray
def insert_x0_and_asmatrix(data):
    ones = pd.DataFrame({'ones': np.ones(len(data))}) #生成一个m行1列的dataFrame
    data = pd.concat([ones,data], axis=1)  #根据列，合并数据
    return data.as_matrix()    #转化为ndarray进行返回

#刷新数据
def shuffleData(data):
    np.random.shuffle(data)
    return data

#读取特征
def get_X(data):
    return data[:,:-1]

#读取输出变量
def get_Y(data):
    return data[:,-1]

data = normalize_feature(data)
data.head()  #打印下特征缩放后的数据看看

	exam1	exam2	admitted
0	-1.594216	0.635141	0
1	-1.817101	-1.201489	0
2	-1.531325	0.359483	0
3	-0.280687	1.080923	1
4	0.688062	0.490905	1

orig_data = insert_x0_and_asmatrix(data)  #加入x0列
orig_data[0:5]

array([[ 1.        , -1.59421626,  0.63514139,  0.        ],
       [ 1.        , -1.81710142, -1.20148852,  0.        ],
       [ 1.        , -1.53132516,  0.35948329,  0.        ],
       [ 1.        , -0.28068724,  1.08092281,  1.        ],
       [ 1.        ,  0.68806193,  0.49090485,  1.        ]])

shuffleData(orig_data)  #打乱样本次序
orig_data[0:5]

array([[ 1.        ,  0.96558389, -1.22094762,  1.        ],
       [ 1.        ,  0.14514418,  1.04248696,  1.        ],
       [ 1.        ,  0.74754551, -1.15162347,  1.        ],
       [ 1.        , -0.5222529 , -1.64944586,  0.        ],
       [ 1.        ,  0.08608101,  0.01976857,  1.        ]])

X = get_X(orig_data)
y = get_Y(orig_data)
theta = np.zeros(3)
X.shape,y.shape,theta

((100, 3), (100,), array([0., 0., 0.]))

sigmoid函数

def sigmoid(z):
    return 1/(1+np.exp(-z))

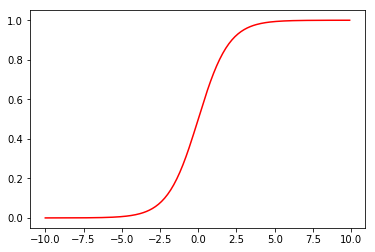
我们来看下sigmoid函数的函数图像

#看下sigmoid函数的函数图像
numbers = np.arange(-10,10,step=0.1)
plt.plot(numbers, sigmoid(numbers),'r')
plt.show()

计算代价函数

#计算代价
def cost(theta, X, y):
    return -np.mean(y * np.log(sigmoid(X @ theta)) 
                    + (1-y) * np.log(1-sigmoid(X @ theta)))

来，我们看下初始状态下，代价值是多少

cost(theta, X, y)

0.6931471805599453

计算梯度

向量化后，得：

\frac{\partial J(\theta)}{\partial \theta} = \frac{1}{m}X^T(Sigmoid(X\theta )-y)

#计算梯度
def gradient(theta, X, y):
    return 1/len(X) * X.T @ (sigmoid(X @ theta) - y)

决策边界

def decision_fun(x,theta):
    coef = -(theta/theta[2])
    print(coef)
    return coef[0] + coef[1]*x

def draw_decision_fun(theta):
    x = np.arange(-2,2,step = 0.01)
    y = decision_fun(x,theta)
    sns.lmplot('exam1','exam2', hue='admitted', data=data, size=6,fit_reg=False,scatter_kws={"s":25})
    plt.plot(x,y)
    plt.xlim(-2,2)
    plt.ylim(-2,2)
    plt.title('Decision Boundary')
    plt.show()

在进行梯度下降算法时，我们有三种不同的停止策略

直接设置迭代次数，次数到了停止迭代
设置一个代价函数下降的阈值，如果本次和上一次迭代完后的代价函数的差值如果小于这个阈值，则停止迭代
设置梯度的阈值，如果某次迭代后，梯度小于阈值，则停止迭代

STOP_ITER = 0  #设置迭代次数
STOP_COST = 1  #设置目标函数下降的阈值
STOP_GRAD = 2  #设置梯度的阈值

def stopCriterion(type, value, threshold):
    #设定三种不同的停止策略
    if type == STOP_ITER:        return value > threshold
    elif type == STOP_COST:      return abs(value[-1]-value[-2]) < threshold
    elif type == STOP_GRAD:      return np.linalg.norm(value) < threshold

#绘制代价函数图像
def drwcosts(costs):
    fig, ax = plt.subplots(figsize=(12,4))
    ax.plot(np.arange(len(costs)), costs, 'r')
    ax.set_xlabel('Iterations')
    ax.set_ylabel('Cost')

下面来实现梯度下降算法

import time
def descent(data, theta, batchSize, stopType, thresh, alpha):
    init_time = time.time()
    i = 0; #迭代次数
    k = 0; #batch
    X = get_X(data)  
    y = get_Y(data)
    grad = gradient(theta,X,y)  #计算梯度
    costs = [cost(theta, X, y)]   #计算代价值
    
    
    while True:
        #根据不同的梯度下降算法（批量，随机，小批量），先计算梯度
        grad = gradient(theta, X[k:k+batchSize],y[k:k+batchSize])
        k = k+batchSize
        if k>= data.shape[0]:
            k = 0
            shuffleData(data)   #重新打乱数据
            X = get_X(data)
            y = get_Y(data)
        theta = theta - alpha * grad  #更新theta
        costs.append(cost(theta, X, y)) #保存本次迭代后的目标值
        i += 1  #迭代次数加1
        
        #根据不同的停止策略，传入不同的value，来判断迭代是否结束
        if stopType == STOP_ITER: 
            value = i
        elif stopType == STOP_COST:
            value = costs
        elif stopType == STOP_GRAD:
            value = grad
         
        if stopCriterion(stopType, value, thresh):  #如果满足停止策略，则停止迭代
            break
    print("theta:",theta)
    print("迭代次数:",i-1)
    print("最后求得的收敛的目标值:",costs[-1])
    print("最后的梯度:",grad)
    print("所用时间:",time.time() - init_time)
    return theta, i-1, costs, grad, time.time() - init_time

不同的停止策略

首先看下，当直接设置迭代次数为5000，学习率为0.0001时，对应模型情况

theat, iter, costs, grad, durtime = descent(orig_data, theta, orig_data.shape[0], STOP_ITER, thresh=5000, alpha=0.0001)
drwcosts(costs)

theta: [0.04702107 0.13181832 0.11768083]
迭代次数: 5000
最后求得的收敛的目标值: 0.6262088600901743
最后的梯度: [-0.08832936 -0.24808112 -0.22154761]
所用时间: 0.8178122043609619

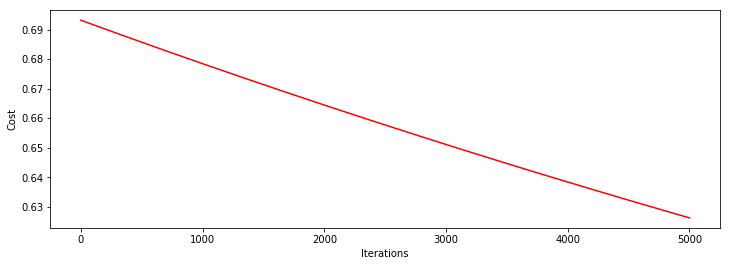
看上面的图像，迭代5000次后，模型远远没到收敛的程度，说明目前还没有近似找到最优解，需要继续增加迭代次数

让我们将迭代次数，加到30000次看看

heat, iter, costs, grad, durtime = descent(orig_data, theta, orig_data.shape[0], STOP_ITER, thresh=30000, alpha=0.0001)
drwcosts(costs)

theta: [0.21656628 0.60953923 0.54481303]
迭代次数: 30000
最后求得的收敛的目标值: 0.44649953741239545
最后的梯度: [-0.05269534 -0.14810478 -0.1325817 ]
所用时间: 4.967716455459595

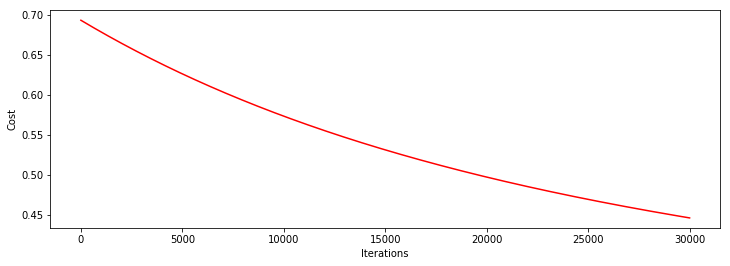
可以看到，相对于上次，这次明显效果稍好点，单是目标函数还是没能很好的收敛，你可以继续增加迭代次数，或者适当增加学习率，进行尝试看看。

下面，我们来换种停止策略，采用设置目标函数下降的阈值这种停止策略看看

设置阈值为0.000001，学习率为0.001

heat, iter, costs, grad, durtime = descent(orig_data, theta, orig_data.shape[0], STOP_COST, thresh=0.000001, alpha=0.001)
drwcosts(costs)

theta: [0.88388452 2.24688547 2.04464801]
迭代次数: 36738
最后求得的收敛的目标值: 0.23470607174751176
最后的梯度: [-0.01016408 -0.02172708 -0.02060574]
所用时间: 6.014917373657227

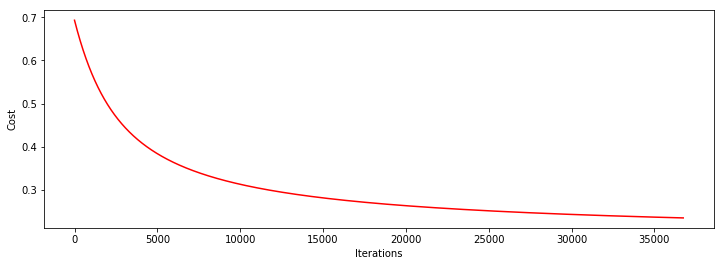
可以看到基本已经收敛。用时6秒钟左右

下面，再来看下设置梯度的阈值这种停止策略下训练出的模型

设置梯度阈值为0.01，学习率为0.001

heat, iter, costs, grad, durtime = descent(orig_data, theta, orig_data.shape[0], STOP_GRAD, thresh=0.01, alpha=0.001)
drwcosts(costs)

theta: [1.31220652 3.14902915 2.90906189]
迭代次数: 112802
最后求得的收敛的目标值: 0.20918126836321715
最后的梯度: [-0.00323388 -0.00681177 -0.00656816]
所用时间: 19.595609664916992

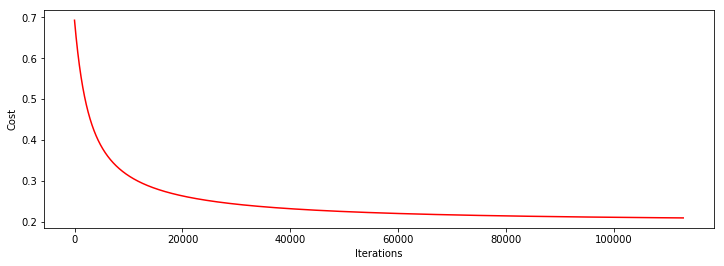
可以看到，这次效果最好，代价函数基本已经收敛，最后的目标值为：0.20918126836321718 迭代了112802次，耗时20秒左右

对比不同的梯度下降方法

上面，我们都用的是批量梯度下降，下面，我们来尝试下随机梯度下降。停止策略采设置梯度阈值，阈值为0.01，学习率为0.001

heat, iter, costs, grad, durtime = descent(orig_data, theta, 1,  STOP_GRAD, thresh=0.01, alpha=0.001)
drwcosts(costs)

theta: [0.67632327 1.78493605 1.61049596]
迭代次数: 20239
最后求得的收敛的目标值: 0.2623021373549509
最后的梯度: [-0.00449379 -0.00741967 -0.00495884]
所用时间: 1.0222656726837158

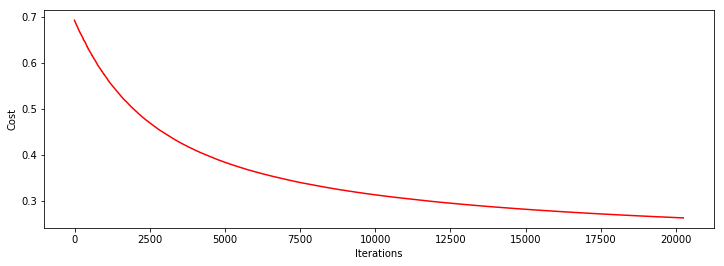
对比上面的批量梯度下降，可以发现，最后模型效果没批量梯度下降好，但是所用时间明显降低了。

但是，需要注意，采用随机梯度下降，并不是每次都能收敛，有时如果样本数据不是很好，可能会出现目标函数无法收敛的情况！

所以，我们更常用批量梯度下降，下面看下

heat, iter, costs, grad, durtime = descent(orig_data, theta, 64,  STOP_GRAD, thresh=0.01, alpha=0.001)
drwcosts(costs)

theta: [0.90249119 2.28523187 2.08373685]
迭代次数: 38617
最后求得的收敛的目标值: 0.2329190821129908
最后的梯度: [-0.00311558 -0.00452799 -0.00279034]
所用时间: 4.404224395751953

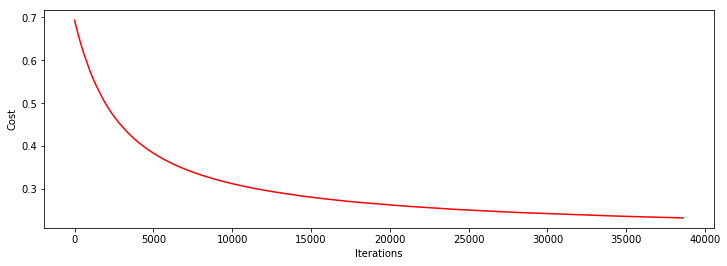
我们可以看到，批量梯度下降所训练出的模型，效果和所用时间，在上述两种下降算法之间。

用训练集预测和验证

def predict(X,theta):   #预测
    prob = sigmoid(X @ theta)
    return (prob >= 0.5).astype(int)

y_predict = predict(X, theat)  #得到训练集数据对应的预测结果
print(classification_report(y, y_predict))
#precision：精确度
#recall：召回率
#f1-score： f1值

             precision    recall  f1-score   support

        0.0       0.88      0.88      0.88        40
        1.0       0.92      0.92      0.92        60

avg / total       0.90      0.90      0.90       100

欢迎关注我的个人公众号 AI计算机视觉工坊，本公众号不定期推送机器学习，深度学习，计算机视觉等相关文章，欢迎大家和我一起学习，交流。

机器学习算法 之逻辑回归以及python实现

逻辑回归(Logistic Regression)

假设函数

目标函数

gradient descent(梯度下降)

决策边界

梯度下降求解逻辑回归问题

数据初始化

sigmoid函数

计算代价函数

计算梯度

决策边界

不同的停止策略

对比不同的梯度下降方法

用训练集预测和验证

机器学习算法之逻辑回归以及python实现