本文包括:二叉搜索树(创建、遍历、搜索、插入等)、JavaScript 实现翻转二叉树
什么是二叉树?
二叉树的定义:二叉树的每个结点至多只有二棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。
二叉查找树(BST):又称为是二叉排序树(Binary Sort Tree)或二叉搜索树。二叉查找树是二叉树的一种,但是它只允许你在左侧节点存储(比父节点)小的值,在右侧节点存储(比父节点)大(或者等于)的值。
创建一个二叉查找树
首先创建一个 BinarySearchTree 类。
// 使用了 ES6 的 Class 语法
class BinarySearchTree {
constructor() {
this.root = null
}
Node(key) {
let left = null
let right = null
return {
key,
left,
right
}
}
}
来看一下二叉查找树的数据结构组织方式(没有找到二叉搜索树的先用二叉树的代替一下):
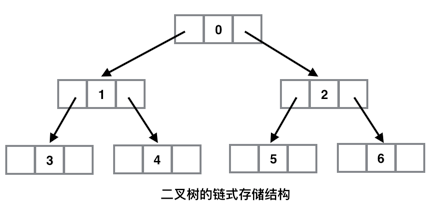
二叉树是通过指针(指向下一个节点)来表示节点之间的关系的,所以需要在声明 Node 的时候,定义两个指针,一个指向左边,一个指向右边。 还需要声明一个 root 来保存树的根元素。
向树中插入一个键(节点)
class BinarySearchTree {
// ...省略前面的
insert (key) {
let newNode = this.Node(key)
if (this.root === null) {
// 如果根节点为空,那么插入的节点就为根节点
this.root = newNode
} else {
// 如果根节点不为空
this.insertNode(this.root, newNode)
}
}
insertNode (node, newNode) {
// 当新节点比父节点小,插入左边
if (newNode.key < node.key) {
// 左边没有内容则插入
if (node.left === null) {
node.left = newNode
} else {
// 有内容就继续递归,直到没有内容然后可以插入
this.insertNode(node.left, newNode)
}
} else {
// 右边和左边相同,不重复说明
if (node.right === null) {
node.right = newNode
} else {
this.insertNode(node.right, newNode)
}
}
}
}
因为使用了 class 所以没有学过 class 的同学可以先看一下 ES6 的 class,再来看文章。
仔细分析上面的代码,多看几遍就可以了解其中的奥妙(也可以自己在游览器中运行一下,插入几个值试一下)。
运行一遍试一下:
let m = new BinarySearchTree()
m.insert(5)
m.insert(4)
m.insert(3)
m.insert(6)
m.insert(7)
会得到这样的结构:
{
key: 5,
left: {
key: 4,
left: {
key: 3,
left: null,
right: null
},
right: null
},
right: {
key: 6,
left: null,
right: {
key: 7,
left: null,
right: null
}
}
}
emmm,真复杂(自己看的都头晕),还是画个图吧。
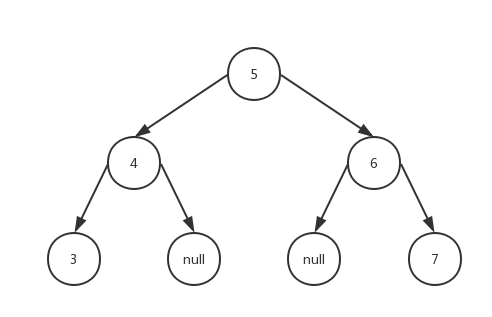
会生成这样一个二叉查找树~,插入功能就算完成啦!
树的遍历
遍历一棵树是指访问树的每个节点并对它们进行某种操作的过程。访问树会有三种方法:中序、先序、后续。下面分别讲解
中序遍历
中序遍历是一种以上行顺序访问 BST 所有节点的遍历方式,也就是从最小到最大的顺序进行访问所有节点。具体方法,看代码吧,配上图多看两遍代码就能明白了(我是这么认为的)。
class BinarySearchTree {
// ...省略前面的
inOrderTraverse (callback) {
this.inOrderTraverseNode(this.root, callback)
}
inOrderTraverseNode (node, callback) {
if (node !== null) {
this.inOrderTraverseNode(node.left, callback)
callback(node.key)
this.inOrderTraverseNode(node.right, callback)
}
}
}
同样,用图展示一下遍历的过程,具体过程看代码多思考一下。
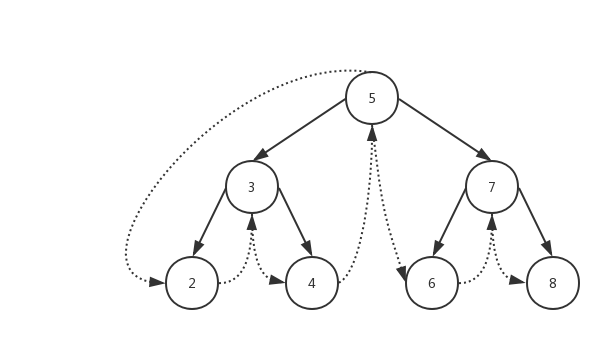
先序遍历
先序遍历会先访问节点本身,然后再访问它的左侧子节点,最后再访问右侧的节点。
class BinarySearchTree {
// ...省略前面的
preOrderTraverse (callback) {
this.preOrderTraverseNode(this.root, callback)
}
preOrderTraverseNode (node, callback) {
if (node !== null) {
callback(node.key)
this.preOrderTraverseNode(node.left, callback)
this.preOrderTraverseNode(node.right, callback)
}
}
}
仔细看代码,发现和中序遍历的区别不过是先执行了 callback 然后再遍历左右。
后序遍历
后序遍历则是先访问节点的后代节点,然后再访问节点本身。实现:
class BinarySearchTree {
// ...省略前面的
postOrderTraverse (callback) {
this.postOrderTraverseNode(this.root, callback)
}
postOrderTraverseNode (node, callback) {
if (node !== null) {
this.postOrderTraverseNode(node.left, callback)
this.postOrderTraverseNode(node.right, callback)
callback(node.key)
}
}
}
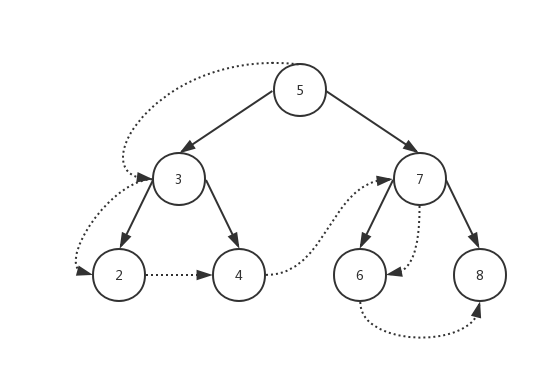
再仔细看代码,发现和中序遍历的区别不过是先执行了遍历了左右,最后执行了 callback 。
惯例,画张图~
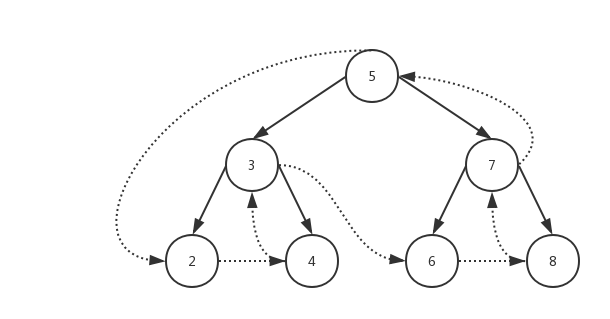
三种遍历方式讲完啦,不懂的可以多看几遍代码哦~
搜索二叉搜索树中的值
在树中,通常有三种经常使用的搜索类型:
- 搜索最大值
- 搜索最小值
- 搜索特定值
下面一一列举
搜索最小和最大值
首先我们知道二叉搜索树中的最小值在最左边,最大值在最右边。既然知道这个,那么实现搜索最大和最小就十分简单了。所以直接上代码:
class BinarySearchTree {
// ...省略前面的
// 搜索最小
min () {
return this.minNode(this.root)
}
minNode (node) {
if (node) {
// 如果节点存在,而且左边不为 null
while (node && node.left !== null) {
node = node.left
}
return node.key
}
// 如果树为空,则返回 null
return null
}
// 搜索最大
max () {
return this.maxNode(this.root)
}
maxNode (node) {
if (node) {
while (node && node.right !== null) {
node = node.right
}
return node.key
}
return null
}
}
搜索特定的值
基本上的思路和遍历节点差不多,具体看代码。
class BinarySearchTree {
// ...省略前面的
search (key) {
return this.searchNode(this.root, key)
}
searchNode (node, key) {
if (node === null) {
return false
}
// 如果 key 比节点的值小,那么搜索左边的子节点,下面的相反
if (key < node.key) {
return this.searchNode(node.left, key)
} else if (key > node.key) {
return this.searchNode(node.right, key)
} else {
return true
}
}
}
翻转二叉树
翻转一个二叉树,直观上看,就是把二叉树的每一层左右顺序倒过来。
例如:
Input:
4
/ \
2 7
/ \ / \
1 3 6 9
Output:
4
/ \
7 2
/ \ / \
9 6 3 1
仔细看就是先把最底下的节点反转,然后上一个节点再翻转。例如:1 - 3 反转成 3 - 1,6 - 9 反转成 9 - 6, 然后再让 2 - 7 反转。当然反过来也一样,先反转 2 - 7 也是可以的。
所以具体的过程是:
- 翻转根节点的左子树(递归调用当前函数)
- 翻转根节点的右子树(递归调用当前函数)
- 交换根节点的左子节点与右子节点
最后看一下实现的代码:
class BinarySearchTree {
// ...省略前面的
invertTree (node = this.root) {
if (node === null) {
return
}
this.invertTree(node.left)
this.invertTree(node.right)
this.exchange(node)
}
exchange (node) {
let temp = node.left
node.left = node.right
node.right = temp
}
}
这样就简单实现啦,舒服舒服~
代码
全部代码在这里~
class BinarySearchTree {
constructor() {
this.root = null
}
Node(key) {
let left = null
let right = null
return {
key,
left,
right
}
}
insert(key) {
let newNode = this.Node(key)
if (this.root === null) {
// 如果根节点为空,那么插入的节点就为根节点
this.root = newNode
} else {
this.insertNode(this.root, newNode)
}
}
insertNode(node, newNode) {
console.log(node)
if (newNode.key < node.key) {
if (node.left === null) {
node.left = newNode
} else {
this.insertNode(node.left, newNode)
}
} else {
if (node.right === null) {
node.right = newNode
} else {
this.insertNode(node.right, newNode)
}
}
}
inOrderTraverse(callback) {
this.inOrderTraverseNode(this.root, callback)
}
inOrderTraverseNode(node, callback) {
if (node !== null) {
this.inOrderTraverseNode(node.left, callback)
callback(node.key)
this.inOrderTraverseNode(node.right, callback)
}
}
preOrderTraverse(callback) {
this.preOrderTraverseNode(this.root, callback)
}
preOrderTraverseNode(node, callback) {
if (node !== null) {
callback(node.key)
this.preOrderTraverseNode(node.left, callback)
this.preOrderTraverseNode(node.right, callback)
}
}
postOrderTraverse(callback) {
this.postOrderTraverseNode(this.root, callback)
}
postOrderTraverseNode(node, callback) {
if (node !== null) {
this.postOrderTraverseNode(node.left, callback)
this.postOrderTraverseNode(node.right, callback)
callback(node.key)
}
}
// 搜索最小
min() {
return this.minNode(this.root)
}
minNode(node) {
if (node) {
// 如果节点存在,而且左边不为 null
while (node && node.left !== null) {
node = node.left
}
return node.key
}
// 如果树为空,则返回 null
return null
}
// 搜索最大
max() {
return this.maxNode(this.root)
}
maxNode(node) {
if (node) {
while (node && node.right !== null) {
node = node.right
}
return node.key
}
return null
}
search(key) {
return this.searchNode(this.root, key)
}
searchNode(node, key) {
console.log('node-', node, '---', node === null, '-key-', key)
if (node === null) {
return false
}
// 如果 key 比节点的值小,那么搜索左边的子节点,下面的相反
if (key < node.key) {
return this.searchNode(node.left, key)
} else if (key > node.key) {
return this.searchNode(node.right, key)
} else {
console.log('didi')
return true
}
}
invertTree (node = this.root) {
if (node === null) {
return
}
this.invertTree(node.left)
this.invertTree(node.right)
this.exchange(node)
}
exchange (node) {
let temp = node.left
node.left = node.right
node.right = temp
}
}
最后
文章是自己的学习的一个记录,如果能够顺便帮助大家学习一下,那就再好不过了。
但是因为本人技术技术有限,所以文章难免会有疏漏,欢迎指出。
参考
- 书籍:《学习 JavaScript 数据结构与算法》
- [数据结构][Leetcode]翻转二叉树