题目
输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。
注意:字符可能重复!
比如,aab的所有排列为,aab,aba,baa
解析
预备知识
全排列:n个数按照一定顺序组成的排列,成为全排列。意思就是所有元素都参与排列。这些排列为n!。因为第一个位置可以放n个元素,当第一个确定以后,第二个位置可以放n-1个元素,依次类推,当前n-1个位置都确定好元素后,最后一个位置只能放1个,故总排列数为n*(n-1)...*1=n!。
思路一
我们先考虑不重复时的情况,因为这种简单一点,先从简单出发。对于给定的字符串,要输出字典序的所有的排列。我们可以dfs的思路来做,确切的说利用全排列的定义来做。为了保证字典序,不妨先对给定字符串排序,这样得到第一个字符串必为最小的。比如213,所有的排列为:123 132 213 231 312 321。
我们的思路就是从高位开始,每一个位置都从1,2,3分别取值,只要高位优先取当前剩余的元素的最小值,就能保证生成的字符串仅挨与上一次。为了记录每一轮中以取的值,添加一个访问数组,该数组记录哪些元素已被访问,其索引对应排序后的字符串索引。简单过程如下:
- 第一个位置从1,2,3开始遍历,取1后,第二位置也从1,2,3遍历,但发现1已被取过,又为了保证最小,所以取,第三个位置也从1,2,3遍历,发现1,2都访问过了,取3,这时组成1,2,3
- 第三个位置已经没有元素可以遍历,故回溯到上一层中,第二个位置取3,第三个位置发现1已被访问,2没被访问,故取3, 这时组成1,3,2.
- 第二位置已经没有元素可以遍历了,故回溯到第一个位置了,之后的过程类似。
当前处理重复元素也很简单,有重复元素只不过会导致有重复的排列加入嘛,直接set去重即可。
/**
* 带重复字符的全排列问题
* 利用set来去重
* @param str
* @return
*/
public static ArrayList<String> Permutation(String str) {
ArrayList<String> result = new ArrayList<>();
if(str == null || str.equals("")) {
return result;
}
char[] chars = str.toCharArray();
Arrays.sort(chars);
Set<String> set = new LinkedHashSet<>();
boolean[] vis = new boolean[chars.length];
char[] temp = new char[chars.length];
permutation(0, temp, chars, set, vis);
result.addAll(set);
return result;
}
/**
* dfs形式遍历字符数组
* 利用访问数组来确定某一位置的元素是否已经访问
* @param index
* @param temp
* @param chars
* @param set
* @param vis
*/
public static void permutation(int index, char[] temp, char[] chars, Set<String> set, boolean[] vis) {
if(index == chars.length) {
set.add(new String(temp));
return;
}
for(int i = 0; i < chars.length; i++) {
if(!vis[i]) {
temp[index] = chars[i];
vis[i] = true;
permutation(index + 1, temp, chars, set, vis);
vis[i] = false;
}
}
}
思路二
另一种思路就是分解子问题了,可以把排列问题分成固定第一个位置,剩余元素全排列问题。之后对剩余元素又进行同样的处理,固定第一个位置,剩余元素全排列。如图:
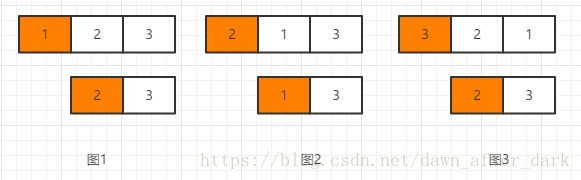
这种思路就无法像思路一可以按字典序生成了,举个例子就明白,比如第一个位置与最后一个元素交换时,那么这时的排列其实是最大的,而这时我们还有其他的排列没有处理呢,所以需要用treeSet来保证插入的字符串按字典序了。
public static ArrayList<String> Permutation2(String str) {
ArrayList<String> result = new ArrayList<>();
if(str == null || str.equals("")) {
return result;
}
char[] chars = str.toCharArray();
Set<String> set = new TreeSet<>();
permutation2(0, chars, set);
result.addAll(set);
return result;
}
public static void permutation2(int index, char[] chars, Set<String> set) {
if(index == chars.length - 1) {
set.add(new String(chars));
return;
}
for(int i = index; i < chars.length; i++) {
swap(chars, index, i);
permutation2(index + 1, chars, set);
swap(chars, index, i);
}
}
public static void swap(char[] chars, int i, int j) {
char temp = chars[i];
chars[i] = chars[j];
chars[j] = temp;
}
上面第二个回溯只不过了是为了回溯时恢复到父问题的原始状态,使的父问题继续与下一个位置交换元素,开始新的子问题。
思路三
思路二能不能优化一下,不产生多余的排列呢。
第一个想法可能就是遇到与第一部分元素相等,就不交换。比如abb, 第一个位置可分别于第二个,第三个位置交换,因为他们都不与a相同,得到 abb, bab, bba。 考察第二位置时,对于bab,第二位置会与第三个位置交换,得到bba。而bba已在与第一位置交换的过程中出现过了。所以单纯的看交换元素是否相等是不行的。
我们发现导致有重复的出现的原因为,已经有b在第一个位置出现过了,不能在有相同的元素交换到此位置上,即不能有重复的元素作为排列问题的第一部分,这肯定会导致重复的子问题产生。所以对于每一个位置遍历,我们添加一个set用于记录以在该位置出现过的元素。
这样就可以不同set了,但是由于没有字典序的保证,最后对结果集还是要做一次排序。
//--------------方法三
public static ArrayList<String> Permutation3(String str) {
ArrayList<String> result = new ArrayList<>();
if(str != null && str.length() > 0) {
permutation3(0, str.toCharArray(), result);
Collections.sort(result);
}
return result;
}
public static void permutation3(int index, char[] chars, ArrayList<String> result) {
if(index == chars.length - 1) {
result.add(new String(chars));
return;
}
//记录该位置已出现过的元素
Set<Character> characters = new HashSet<>();
for(int i = index; i < chars.length; i++) {
if(!(i != index && characters.contains(chars[i]))) {
characters.add(chars[i]);
swap(chars, index, i);
permutation3(index + 1, chars, result);
swap(chars, index, i);
}
}
}
public static void swap(char[] chars, int i, int j) {
char temp = chars[i];
chars[i] = chars[j];
chars[j] = temp;
}
思路四
思路四就是大名鼎鼎的字典序算法了啊。该算法基于逆序的思想。
逆序就是只序列中存在较大值在较小值的前面,逆序数就是一个序列中这样的组合有几对。
对于一个排列12345,我们知道当逆序产生的位置越高,该排列的位置越靠后,对应的字典序也就越大。比如12534,逆序产生的位置在第三个位置;51234,逆序的位置产生在最高位第一个位置,故比12534大。结论: 逆序位置越高和逆序对越多,该排列位置越靠后,54321即为最大。
字典序算法如下:
- 对当前数列中从后往前找到第一个正序对,并记录该正序对位置A。
- 从后往前找第一个大于该位置的元素,并记录该位置B。
- 交换两个位置的元素
- 对【A+1, 总长度】的所有元素变为正序。
为什么要找到第一个正序对?
寻找当前排列的下一个排列,其实就是增加一个逆序对,或者逆序位置向高处移动。在我们找到正序的位置后,说明该位置为当前逆序的前一个位置。所以我们只要在该位置产生一个逆序,就会比原排列大。
为什么要从后往前找第一个大于正序位置的元素?
因为为了仅仅比原排列大,所以只要产生最小的逆序即可,最小逆序即为刚刚比正序位置的上数大即可。那么为什么第一个大于就行呢,在我们找第一个正序对的时候,已遍历过的位置都是逆序时,也就是第一个大于即为刚刚大于,之后都是比位置A元素大的。
为什么最后还要把原逆序区间恢复为正序呢?
因为我们已经将逆序往高位移动了,所以后面部分保持最小字典序即可保证新排列仅大于原排列。
//-----------方法四 字典序算法---------
public static ArrayList<String> Permutation4(String str) {
ArrayList<String> result = new ArrayList<>();
if(str != null && str.length() > 0) {
char[] chars = str.toCharArray();
Arrays.sort(chars);
result.add(new String(chars));
while(true) {
int firstPositiveOrder = chars.length - 2;
while(firstPositiveOrder >= 0
&& chars[firstPositiveOrder] >= chars[firstPositiveOrder + 1]) {
firstPositiveOrder--;
}
if(firstPositiveOrder == -1) {
break;
}
int index = chars.length - 1;
while(chars[index] <= chars[firstPositiveOrder]) {
index--;
}
swap(chars, firstPositiveOrder, index);
reverse(chars, firstPositiveOrder + 1, chars.length);
result.add(new String(chars));
}
}
return result;
}
public static void reverse(char[] chars, int begin, int end) {
for (int i = begin, j = end - 1; i < j; i++, j--) {
swap(chars, i, j);
}
}
总结
对于这种多个字符按某种顺序求解的问题, 都可以用全排列的思想来做。