之前相关文章目录:
- 机器学习 之线性回归
- 机器学习 之逻辑回归及python实现
- 机器学习项目实战 交易数据异常检测
- 机器学习之 决策树(Decision Tree)
- 机器学习之 决策树(Decision Tree)python实现
- 机器学习之 PCA(主成分分析)
- 机器学习之特征工程
说到特征工程,就不得不提有这么一句话在业界广泛流传:数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已,从而可见,特征工程的重要程度。
一.特征工程的解释和意义
那么什么是特征工程?首先先看下特征,
特征: 是指数据中抽取出来的对结果预测有用的信息,也就是数据的相关属性。
特征工程:使用专业背景知识和技巧处理数据,使得 特征能在机器学习算法上发挥更好的作用的过程
意义:
1.更好的特征意味着更强的灵活度
2.更好的特征意味着只需用简单模型,就可以训练出很好的效果
3.更好的特征意味着可以训练出更好的结果
二.特征工程具体流程
整个流程可以用下面这种图来概括
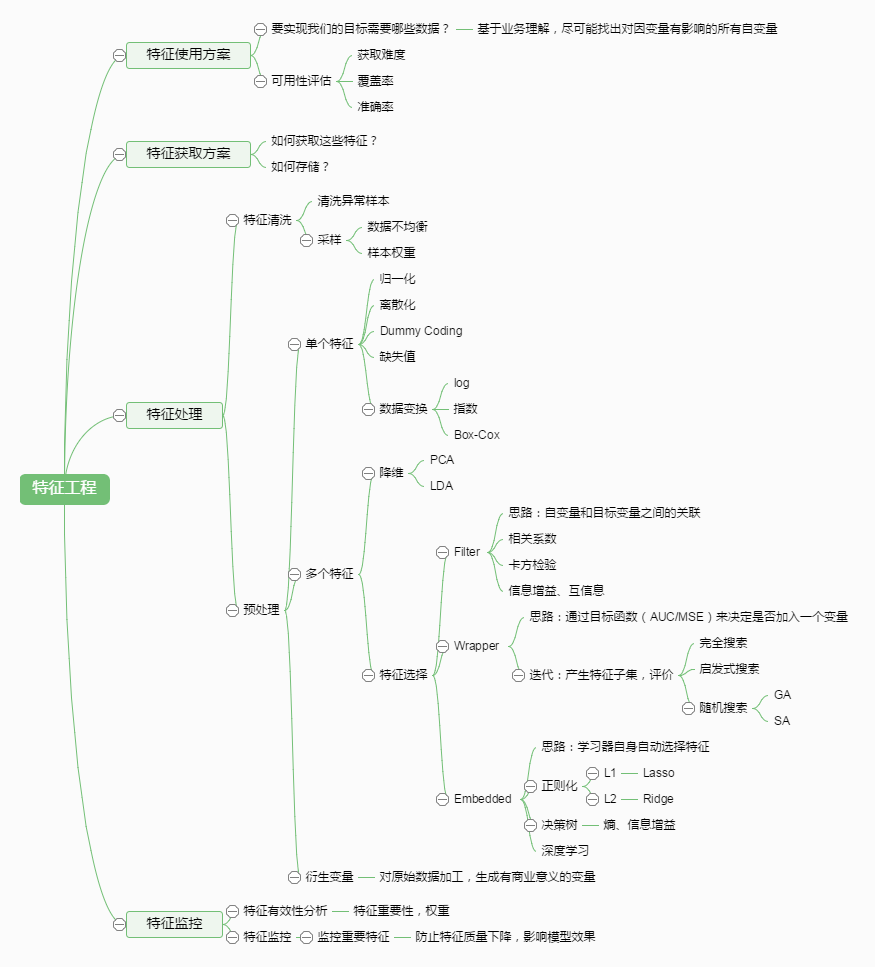
1.特征使用方案
在确定好我们的目标后,我们首先要做的就是根据业务场景,分析要实现我们的目标需要哪些数据。也就是基于业务理解,尽可能找出对因变量有影响的所有自变量。 比如:我现在要预测用户对商品的下单情况,或者我要给 用户做商品推荐,那我需要采集什么信息呢? 可以分为三个方向去采集,
- 店家:店家的类别,店家评分,店家所用快递等
- 商品:商品的类别,评分,购买人数,颜色等
- 用户:历史购买信息,消费能力,购物车转换比,商品停留时间,用户年龄,所在地址等
然后,我们针对我们所需要的数据,需要进行可用性评估
- 获取难度,数据我们能够采集到吗? 比如对于用户年龄来说,就比较难于获取,并不是每个人都在注册时都会去填写年龄
- 覆盖率,有些数据并不是每个对象都有的,比如对于历史购买信息,对于新用户来说,是没有的
- 准确率, 像用户年龄,店家评分,也都会有准确率的问题,因为店家可能刷单,用户也可能不写真实年龄
- 线上实时计算的时候获取是否快捷?
2.特征获取方案
在确定好我们需要的特征之后,接下来就要进行考虑特征的获取和存储,主要分为离线特征获取和在线特征获取
1 离线特征获取方案
离线可以使用海量的数据,借助于分布式文件存储平台,例如HDFS等,使用例如MapReduce,Spark等处理工具来处理海量的数据等。
2 在线特征获取方案
在线特征比较注重获取数据的延时,由于是在线服务,需要在非常短的时间内获取到相应的数据,对查找性能要求非常高,可以将数据存储在索引、kv存储等。而查找性能与数据的数据量会有矛盾,需要折衷处理,我们使用了特征分层获取方案,如下图所示。
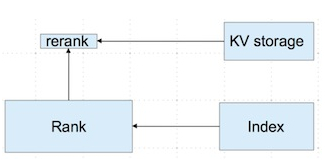
3.特征处理
接下来就是特征工程中最重要的,也是我们主要在做的,特征处理了
3.1特征清洗
在特征处理中,首先需要进行的是特征清洗,主要做两件事情
3.1.1清洗脏数据(异常数据)
如何检测异常数据呢?主要有下面几种
1.基于统计的异常点检测算法
(1).简单统计分析:
比如对属性值进行一个描述性的统计,从而查看哪些值是不合理的,比如针对年龄来说,我们规定范围维 [0,100],则不在这个范围的样本,则就认为是异常样本
(2).3δ原则(δ为方差):
当数据服从正态分布:根据正态分布的定义可知,距离平均值3δ之外的概率为 P(|x-μ|>3δ) <= 0.003 ,这属于极小概率事件,在默认情况下我们可以认定,距离超过平均值3δ的样本是不存在的。 因此,当样本距离平均值大于3δ,则认定该样本为异常值
(3).通过极差和四分位数间距,进行异常数据的检测
2.基于距离的异常点检测算法(其实和K近邻算法的思想一样)
主要通过距离方法来检测异常点,将一个数据点与大多数点之间距离大于某个阈值的点视为异常点,主要使用的距离度量方法有绝对距离(曼哈顿距离)、欧氏距离和马氏距离等方法
3.基于密度的异常点检测算法
考察当前点周围密度,可以发现局部异常点
3.1.2缺失值处理
对于一个特征来说
- 如果所有样本中的的缺失值极多,则可以直接去掉
- 如果缺失值不是很多,可以考虑用全局均值,或者中位数进行填充
- 将此特征作为目标,根据未缺失的数据,利用相关算法模型,对缺失值进行预测
3.1.3数据采样
数据采样主要是为了处理样本不均衡问题的。比如有些情况下,获取来的数据,正负样本个数差距很大,而大多数模型对正负样本比是敏感的(比如逻辑回归),所以,需要通过数据采样,来使数据正负样本均衡
在处理样本不均衡问题时,主要分为两种情况
-
正负样本个数差距很大,并且同时正负样本个数本身也很大,这个时候可以采取下采样方法。
下采样:对训练集里面样本数量较多的类别(多数类)进行欠采样,抛弃一些样本来缓解类不平衡。 -
正负样本个数差距很大,并且同时正负样本个数本身比较小,这个时候可以采取上采样方法。
上采样:对训练集里面样本数量较少的类别(少数类)进行过采样,合成新的样本来缓解类不平衡。 这个时候会用到一个非常经典的过采样算法SMOTE(关于过采样SMOTE算法,在之前的一篇文章中(机器学习项目实战 交易数据异常检测),里面有进行说明和应用,在这块不再重复)
3.2特征预处理
对于不同类型的特征,处理方式不同,下面分别来概述
3.2.1数值型(指的是连续型数据)
数值型特征,一般需要做以下几个方面处理
1.1统计值。
需要查看对应特征的最大值,最小值,平均值,方差等,从而对数据进行更好的分析,
下面以sklearn中的自带的鸢尾花数据集为例,通过代码来演示
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
iris = load_iris() #获取数据集
# iris.data[:5] # 展示数据集的前5个数据
series = pd.Series(iris.data[:,0])
series.describe() #通过describe方法,可以直接获得当前特征下数据的总数,均值,方差,各个分位数,以及最大最小值等
count 150.000000
mean 5.843333
std 0.828066
min 4.300000
25% 5.100000
50% 5.800000
75% 6.400000
max 7.900000
dtype: float64
1.2.无量纲化。 常用的无量纲化方法有标准化和区间缩放法。
(1).标准化:标准化需要计算对应特征下数据的均值和方差,然后看当前特征下每个值距离均值多少个方差,具体公式如下:
(2).区间缩放法:区间缩放法的思路有多种,常见的一种为利用两个最值进行缩放,具体公式如下:
(3)标准化和归一化的区别:可以这样来区分,对于一个m个样本,n个特征的m*n的特征矩阵,一行表示的是一个样本数据,包含n个特征,一列表示一个特征下的m个样本数据。上面所说的标准化是针对的特征矩阵的列处理数据,将样本的特征值转换到同一量纲下,而归一化则是依据特征矩阵的行进行处理数据,如果将一行数据看做一个向量的化,相当于向量的单位化
上面两个方法(标准化和区间缩放分),sklearn中已经帮我们封装好了,具体代码如下
from sklearn.preprocessing import StandardScaler
StandardScaler().fit_transform(iris.data) #标准化
from sklearn.preprocessing import MinMaxScaler
MinMaxScaler().fit_transform(iris.data)
array([[0.22222222, 0.625 , 0.06779661, 0.04166667],
[0.16666667, 0.41666667, 0.06779661, 0.04166667],
[0.11111111, 0.5 , 0.05084746, 0.04166667],
[0.08333333, 0.45833333, 0.08474576, 0.04166667],
[0.19444444, 0.66666667, 0.06779661, 0.04166667],
[0.30555556, 0.79166667, 0.11864407, 0.125 ],
[0.08333333, 0.58333333, 0.06779661, 0.08333333],
[0.19444444, 0.58333333, 0.08474576, 0.04166667],
[0.02777778, 0.375 , 0.06779661, 0.04166667],
[0.16666667, 0.45833333, 0.08474576, 0. ],
[0.30555556, 0.70833333, 0.08474576, 0.04166667],
[0.13888889, 0.58333333, 0.10169492, 0.04166667],
[0.13888889, 0.41666667, 0.06779661, 0. ],
[0. , 0.41666667, 0.01694915, 0. ],
[0.41666667, 0.83333333, 0.03389831, 0.04166667],
[0.38888889, 1. , 0.08474576, 0.125 ],
[0.30555556, 0.79166667, 0.05084746, 0.125 ],
[0.22222222, 0.625 , 0.06779661, 0.08333333],
[0.38888889, 0.75 , 0.11864407, 0.08333333],
[0.22222222, 0.75 , 0.08474576, 0.08333333],
[0.30555556, 0.58333333, 0.11864407, 0.04166667],
[0.22222222, 0.70833333, 0.08474576, 0.125 ],
[0.08333333, 0.66666667, 0. , 0.04166667],
[0.22222222, 0.54166667, 0.11864407, 0.16666667],
[0.13888889, 0.58333333, 0.15254237, 0.04166667],
[0.19444444, 0.41666667, 0.10169492, 0.04166667],
[0.19444444, 0.58333333, 0.10169492, 0.125 ],
[0.25 , 0.625 , 0.08474576, 0.04166667],
[0.25 , 0.58333333, 0.06779661, 0.04166667],
[0.11111111, 0.5 , 0.10169492, 0.04166667],
[0.13888889, 0.45833333, 0.10169492, 0.04166667],
[0.30555556, 0.58333333, 0.08474576, 0.125 ],
[0.25 , 0.875 , 0.08474576, 0. ],
[0.33333333, 0.91666667, 0.06779661, 0.04166667],
[0.16666667, 0.45833333, 0.08474576, 0. ],
[0.19444444, 0.5 , 0.03389831, 0.04166667],
[0.33333333, 0.625 , 0.05084746, 0.04166667],
[0.16666667, 0.45833333, 0.08474576, 0. ],
[0.02777778, 0.41666667, 0.05084746, 0.04166667],
[0.22222222, 0.58333333, 0.08474576, 0.04166667],
[0.19444444, 0.625 , 0.05084746, 0.08333333],
[0.05555556, 0.125 , 0.05084746, 0.08333333],
[0.02777778, 0.5 , 0.05084746, 0.04166667],
[0.19444444, 0.625 , 0.10169492, 0.20833333],
[0.22222222, 0.75 , 0.15254237, 0.125 ],
[0.13888889, 0.41666667, 0.06779661, 0.08333333],
[0.22222222, 0.75 , 0.10169492, 0.04166667],
[0.08333333, 0.5 , 0.06779661, 0.04166667],
[0.27777778, 0.70833333, 0.08474576, 0.04166667],
[0.19444444, 0.54166667, 0.06779661, 0.04166667],
[0.75 , 0.5 , 0.62711864, 0.54166667],
[0.58333333, 0.5 , 0.59322034, 0.58333333],
[0.72222222, 0.45833333, 0.66101695, 0.58333333],
[0.33333333, 0.125 , 0.50847458, 0.5 ],
[0.61111111, 0.33333333, 0.61016949, 0.58333333],
[0.38888889, 0.33333333, 0.59322034, 0.5 ],
[0.55555556, 0.54166667, 0.62711864, 0.625 ],
[0.16666667, 0.16666667, 0.38983051, 0.375 ],
[0.63888889, 0.375 , 0.61016949, 0.5 ],
[0.25 , 0.29166667, 0.49152542, 0.54166667],
[0.19444444, 0. , 0.42372881, 0.375 ],
[0.44444444, 0.41666667, 0.54237288, 0.58333333],
[0.47222222, 0.08333333, 0.50847458, 0.375 ],
[0.5 , 0.375 , 0.62711864, 0.54166667],
[0.36111111, 0.375 , 0.44067797, 0.5 ],
[0.66666667, 0.45833333, 0.57627119, 0.54166667],
[0.36111111, 0.41666667, 0.59322034, 0.58333333],
[0.41666667, 0.29166667, 0.52542373, 0.375 ],
[0.52777778, 0.08333333, 0.59322034, 0.58333333],
[0.36111111, 0.20833333, 0.49152542, 0.41666667],
[0.44444444, 0.5 , 0.6440678 , 0.70833333],
[0.5 , 0.33333333, 0.50847458, 0.5 ],
[0.55555556, 0.20833333, 0.66101695, 0.58333333],
[0.5 , 0.33333333, 0.62711864, 0.45833333],
[0.58333333, 0.375 , 0.55932203, 0.5 ],
[0.63888889, 0.41666667, 0.57627119, 0.54166667],
[0.69444444, 0.33333333, 0.6440678 , 0.54166667],
[0.66666667, 0.41666667, 0.6779661 , 0.66666667],
[0.47222222, 0.375 , 0.59322034, 0.58333333],
[0.38888889, 0.25 , 0.42372881, 0.375 ],
[0.33333333, 0.16666667, 0.47457627, 0.41666667],
[0.33333333, 0.16666667, 0.45762712, 0.375 ],
[0.41666667, 0.29166667, 0.49152542, 0.45833333],
[0.47222222, 0.29166667, 0.69491525, 0.625 ],
[0.30555556, 0.41666667, 0.59322034, 0.58333333],
[0.47222222, 0.58333333, 0.59322034, 0.625 ],
[0.66666667, 0.45833333, 0.62711864, 0.58333333],
[0.55555556, 0.125 , 0.57627119, 0.5 ],
[0.36111111, 0.41666667, 0.52542373, 0.5 ],
[0.33333333, 0.20833333, 0.50847458, 0.5 ],
[0.33333333, 0.25 , 0.57627119, 0.45833333],
[0.5 , 0.41666667, 0.61016949, 0.54166667],
[0.41666667, 0.25 , 0.50847458, 0.45833333],
[0.19444444, 0.125 , 0.38983051, 0.375 ],
[0.36111111, 0.29166667, 0.54237288, 0.5 ],
[0.38888889, 0.41666667, 0.54237288, 0.45833333],
[0.38888889, 0.375 , 0.54237288, 0.5 ],
[0.52777778, 0.375 , 0.55932203, 0.5 ],
[0.22222222, 0.20833333, 0.33898305, 0.41666667],
[0.38888889, 0.33333333, 0.52542373, 0.5 ],
[0.55555556, 0.54166667, 0.84745763, 1. ],
[0.41666667, 0.29166667, 0.69491525, 0.75 ],
[0.77777778, 0.41666667, 0.83050847, 0.83333333],
[0.55555556, 0.375 , 0.77966102, 0.70833333],
[0.61111111, 0.41666667, 0.81355932, 0.875 ],
[0.91666667, 0.41666667, 0.94915254, 0.83333333],
[0.16666667, 0.20833333, 0.59322034, 0.66666667],
[0.83333333, 0.375 , 0.89830508, 0.70833333],
[0.66666667, 0.20833333, 0.81355932, 0.70833333],
[0.80555556, 0.66666667, 0.86440678, 1. ],
[0.61111111, 0.5 , 0.69491525, 0.79166667],
[0.58333333, 0.29166667, 0.72881356, 0.75 ],
[0.69444444, 0.41666667, 0.76271186, 0.83333333],
[0.38888889, 0.20833333, 0.6779661 , 0.79166667],
[0.41666667, 0.33333333, 0.69491525, 0.95833333],
[0.58333333, 0.5 , 0.72881356, 0.91666667],
[0.61111111, 0.41666667, 0.76271186, 0.70833333],
[0.94444444, 0.75 , 0.96610169, 0.875 ],
[0.94444444, 0.25 , 1. , 0.91666667],
[0.47222222, 0.08333333, 0.6779661 , 0.58333333],
[0.72222222, 0.5 , 0.79661017, 0.91666667],
[0.36111111, 0.33333333, 0.66101695, 0.79166667],
[0.94444444, 0.33333333, 0.96610169, 0.79166667],
[0.55555556, 0.29166667, 0.66101695, 0.70833333],
[0.66666667, 0.54166667, 0.79661017, 0.83333333],
[0.80555556, 0.5 , 0.84745763, 0.70833333],
[0.52777778, 0.33333333, 0.6440678 , 0.70833333],
[0.5 , 0.41666667, 0.66101695, 0.70833333],
[0.58333333, 0.33333333, 0.77966102, 0.83333333],
[0.80555556, 0.41666667, 0.81355932, 0.625 ],
[0.86111111, 0.33333333, 0.86440678, 0.75 ],
[1. , 0.75 , 0.91525424, 0.79166667],
[0.58333333, 0.33333333, 0.77966102, 0.875 ],
[0.55555556, 0.33333333, 0.69491525, 0.58333333],
[0.5 , 0.25 , 0.77966102, 0.54166667],
[0.94444444, 0.41666667, 0.86440678, 0.91666667],
[0.55555556, 0.58333333, 0.77966102, 0.95833333],
[0.58333333, 0.45833333, 0.76271186, 0.70833333],
[0.47222222, 0.41666667, 0.6440678 , 0.70833333],
[0.72222222, 0.45833333, 0.74576271, 0.83333333],
[0.66666667, 0.45833333, 0.77966102, 0.95833333],
[0.72222222, 0.45833333, 0.69491525, 0.91666667],
[0.41666667, 0.29166667, 0.69491525, 0.75 ],
[0.69444444, 0.5 , 0.83050847, 0.91666667],
[0.66666667, 0.54166667, 0.79661017, 1. ],
[0.66666667, 0.41666667, 0.71186441, 0.91666667],
[0.55555556, 0.20833333, 0.6779661 , 0.75 ],
[0.61111111, 0.41666667, 0.71186441, 0.79166667],
[0.52777778, 0.58333333, 0.74576271, 0.91666667],
[0.44444444, 0.41666667, 0.69491525, 0.70833333]])
1.3.离散化
离散化是数值型特征非常重要的一个处理,其实就是要将数值型数据转化成类别型数据
连续值的取值空间可能是无穷的,为了便于表示和在模型中处理,需要对连续值特征进行离散化处理
在工业界,很少直接将连续值作为特征喂给逻辑回归模型,而是将连续特征离散化为一系列0、1特征交给逻辑回归模型,这样做的优势有以下几点:
-
稀疏向量内积乘法运算速度快,计算结果方便存储,容易scalable(扩展)。
-
离散化后的特征对异常数据有很强的鲁棒性:比如一个特征是年龄>30是1,否则0。如果特征没有离散化,一个异常数据“年龄300岁”会给模型造成很大的干扰。
-
逻辑回归属于广义线性模型,表达能力受限;单变量离散化为N个后,每个变量有单独的权重,相当于为模型引入了非线性,能够提升模型表达能力,加大拟合。
-
离散化后可以进行特征交叉,由M N个变量变为M*N个变量,进一步引入非线性,提升表达能力。
-
特征离散化后,模型会更稳定,比如如果对用户年龄离散化,20-30作为一个区间,不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反,所以怎么划分区间是门学问。
常用的离散化方法包括等值划分和等量划分。
(1).等值划分是将特征按照值域进行均分,每一段内的取值等同处理。例如某个特征的取值范围为[0,10],我们可以将其划分为10段,[0,1),[1,2),...,[9,10)。
(2).等量划分是根据样本总数进行均分,每段等量个样本划分为1段。例如距离特征,取值范围[0,3000000],现在需要切分成10段,如果按照等比例划分的话,会发现绝大部分样本都在第1段中。使用等量划分就会避免这种问题,最终可能的切分是[0,100),[100,300),[300,500),..,[10000,3000000],前面的区间划分比较密,后面的比较稀疏
下面看下代码实现
ages = np.array([20, 22,25,27,21,23,37,31,61,45,41,32]) #一些年龄数据
# 通过 pandas中的cut方法可以分割数据
# factory = pd.cut(ages,4) #arr原始数据 , 4:要分割成几段
factory = pd.cut(ages,4,labels=['Youth', 'YoungAdult', 'MiddleAged', 'Senior']) #lable,对于每个类别可以自己命名
# factory = pd.cut(arr,bins=[18,25,35,60,100],labels=['a','b','c','d']) #bins 自己指定的分割界限
# factory.dtype #CategoricalDtype,可以看到,cut后返回的是一个Categorical 类型的对象
test = np.array(factory) #获取出分类后的数据
test
# factory.codes # array([0, 0, 0, 0, 0, 0, 1, 1, 3, 2, 2, 1], dtype=int8)
array(['Youth', 'Youth', 'Youth', 'Youth', 'Youth', 'Youth', 'YoungAdult',
'YoungAdult', 'Senior', 'MiddleAged', 'MiddleAged', 'YoungAdult'],
dtype=object)
# 下面看下等量划分
# 通过 pandas中的qcut方法可以分割数据
factory = pd.qcut(ages,4)
# factory
factory.value_counts() #可以看到,通过等量划分,每个类别中的数据个数都一样
(19.999, 22.75] 3
(22.75, 29.0] 3
(29.0, 38.0] 3
(38.0, 61.0] 3
dtype: int64
3.2.2类别型数据
one-hot编码
对于类别型数据,最主要的一个处理,就是进行one-hot编码,看具体例子
# 创建一个简单的原始数据
testdata = pd.DataFrame({'age':[4,6,3,3],'pet':['cat','dog','dog','fish']})
testdata
| age | pet | |
|---|---|---|
| 0 | 4 | cat |
| 1 | 6 | dog |
| 2 | 3 | dog |
| 3 | 3 | fish |
#第一种方法,通过pandas中的提供的get_dummies方法
pd.get_dummies(testdata,columns=['pet']) #第一个参数为原始数据,columns传入需要编码转换的特征,可以为多个,返回新的数据
| age | pet_cat | pet_dog | pet_fish | |
|---|---|---|---|---|
| 0 | 4 | 1 | 0 | 0 |
| 1 | 6 | 0 | 1 | 0 |
| 2 | 3 | 0 | 1 | 0 |
| 3 | 3 | 0 | 0 | 1 |
testdata.pet.values.reshape(-1,1)
array([['cat'],
['dog'],
['dog'],
['fish']], dtype=object)
#第二种方法,使用sklearn中的OneHotEncoder方法
from sklearn.preprocessing import OneHotEncoder
OneHotEncoder().fit_transform(testdata.age.values.reshape(-1,1)).toarray()
array([[0., 1., 0.],
[0., 0., 1.],
[1., 0., 0.],
[1., 0., 0.]])
#OneHotEncoder不能对String型的数值做处理,对String类型做处理的话需要先进行转换
# OneHotEncoder().fit_transform(testdata.pet.values.reshape(-1,1)).toarray() #会报错
from sklearn.preprocessing import LabelEncoder
petvalue = LabelEncoder().fit_transform(testdata.pet)
print(petvalue) # [0 1 1 2] 将字符串类别转换成整型类别
OneHotEncoder().fit_transform(petvalue.reshape(-1,1)).toarray() #可以看到结果和上面通过get_dummies转换出的结果相同
[0 1 1 2]
array([[1., 0., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 0., 1.]])
3.2.3时间型数据
对于时间型数据来说,即可以把它转换成连续值,也可以转换成离散值。
连续值
比如持续时间(单页浏览时长),间隔时间(上次购买/点击离现在的时间)
离散值
比如一天中哪个时间段(hour_0-23) ,一周中星期几(week_monday...) ,一年中哪个星期 ,工作日/周末 , 一年中哪个季度 等
#下面看个例子,这个数据是一个2年内按小时做的自行车租赁数据
import pandas as pd
data = pd.read_csv('kaggle_bike_competition_train.csv', header = 0, error_bad_lines=False)
data.head() #先看下数据的样子,打印前5行
| datetime | season | holiday | workingday | weather | temp | atemp | humidity | windspeed | casual | registered | count | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2011-01-01 00:00:00 | 1 | 0 | 0 | 1 | 9.84 | 14.395 | 81 | 0.0 | 3 | 13 | 16 |
| 1 | 2011-01-01 01:00:00 | 1 | 0 | 0 | 1 | 9.02 | 13.635 | 80 | 0.0 | 8 | 32 | 40 |
| 2 | 2011-01-01 02:00:00 | 1 | 0 | 0 | 1 | 9.02 | 13.635 | 80 | 0.0 | 5 | 27 | 32 |
| 3 | 2011-01-01 03:00:00 | 1 | 0 | 0 | 1 | 9.84 | 14.395 | 75 | 0.0 | 3 | 10 | 13 |
| 4 | 2011-01-01 04:00:00 | 1 | 0 | 0 | 1 | 9.84 | 14.395 | 75 | 0.0 | 0 | 1 | 1 |
#下面我们只看datatime这个时间类型属性,
#首先,我们可以将它切分成
data = data.iloc[:,:1] #只看datatime这个属性
temp = pd.DatetimeIndex(data['datetime'])
data['date'] = temp.date #日期
data['time'] = temp.time #时间
data['year'] = temp.year #年
data['month'] = temp.month #月
data['day'] = temp.day #日
data['hour'] = temp.hour #小时
data['dayofweek'] = temp.dayofweek #具体星期几
data['dateDays'] = (data.date - data.date[0]) #生成一个时间长度特征 ['0days','0days',...,'1days',...]
data['dateDays'] = data['dateDays'].astype('timedelta64[D]') #转换成float型
data
| datetime | date | time | year | month | day | hour | dayofweek | dateDays | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 2011-01-01 00:00:00 | 2011-01-01 | 00:00:00 | 2011 | 1 | 1 | 0 | 5 | 0.0 |
| 1 | 2011-01-01 01:00:00 | 2011-01-01 | 01:00:00 | 2011 | 1 | 1 | 1 | 5 | 0.0 |
| 2 | 2011-01-01 02:00:00 | 2011-01-01 | 02:00:00 | 2011 | 1 | 1 | 2 | 5 | 0.0 |
| 3 | 2011-01-01 03:00:00 | 2011-01-01 | 03:00:00 | 2011 | 1 | 1 | 3 | 5 | 0.0 |
| 4 | 2011-01-01 04:00:00 | 2011-01-01 | 04:00:00 | 2011 | 1 | 1 | 4 | 5 | 0.0 |
| 5 | 2011-01-01 05:00:00 | 2011-01-01 | 05:00:00 | 2011 | 1 | 1 | 5 | 5 | 0.0 |
| 6 | 2011-01-01 06:00:00 | 2011-01-01 | 06:00:00 | 2011 | 1 | 1 | 6 | 5 | 0.0 |
| 7 | 2011-01-01 07:00:00 | 2011-01-01 | 07:00:00 | 2011 | 1 | 1 | 7 | 5 | 0.0 |
| 8 | 2011-01-01 08:00:00 | 2011-01-01 | 08:00:00 | 2011 | 1 | 1 | 8 | 5 | 0.0 |
| 9 | 2011-01-01 09:00:00 | 2011-01-01 | 09:00:00 | 2011 | 1 | 1 | 9 | 5 | 0.0 |
| 10 | 2011-01-01 10:00:00 | 2011-01-01 | 10:00:00 | 2011 | 1 | 1 | 10 | 5 | 0.0 |
| 11 | 2011-01-01 11:00:00 | 2011-01-01 | 11:00:00 | 2011 | 1 | 1 | 11 | 5 | 0.0 |
| 12 | 2011-01-01 12:00:00 | 2011-01-01 | 12:00:00 | 2011 | 1 | 1 | 12 | 5 | 0.0 |
| 13 | 2011-01-01 13:00:00 | 2011-01-01 | 13:00:00 | 2011 | 1 | 1 | 13 | 5 | 0.0 |
| 14 | 2011-01-01 14:00:00 | 2011-01-01 | 14:00:00 | 2011 | 1 | 1 | 14 | 5 | 0.0 |
| 15 | 2011-01-01 15:00:00 | 2011-01-01 | 15:00:00 | 2011 | 1 | 1 | 15 | 5 | 0.0 |
| 16 | 2011-01-01 16:00:00 | 2011-01-01 | 16:00:00 | 2011 | 1 | 1 | 16 | 5 | 0.0 |
| 17 | 2011-01-01 17:00:00 | 2011-01-01 | 17:00:00 | 2011 | 1 | 1 | 17 | 5 | 0.0 |
| 18 | 2011-01-01 18:00:00 | 2011-01-01 | 18:00:00 | 2011 | 1 | 1 | 18 | 5 | 0.0 |
| 19 | 2011-01-01 19:00:00 | 2011-01-01 | 19:00:00 | 2011 | 1 | 1 | 19 | 5 | 0.0 |
| 20 | 2011-01-01 20:00:00 | 2011-01-01 | 20:00:00 | 2011 | 1 | 1 | 20 | 5 | 0.0 |
| 21 | 2011-01-01 21:00:00 | 2011-01-01 | 21:00:00 | 2011 | 1 | 1 | 21 | 5 | 0.0 |
| 22 | 2011-01-01 22:00:00 | 2011-01-01 | 22:00:00 | 2011 | 1 | 1 | 22 | 5 | 0.0 |
| 23 | 2011-01-01 23:00:00 | 2011-01-01 | 23:00:00 | 2011 | 1 | 1 | 23 | 5 | 0.0 |
| 24 | 2011-01-02 00:00:00 | 2011-01-02 | 00:00:00 | 2011 | 1 | 2 | 0 | 6 | 1.0 |
| 25 | 2011-01-02 01:00:00 | 2011-01-02 | 01:00:00 | 2011 | 1 | 2 | 1 | 6 | 1.0 |
| 26 | 2011-01-02 02:00:00 | 2011-01-02 | 02:00:00 | 2011 | 1 | 2 | 2 | 6 | 1.0 |
| 27 | 2011-01-02 03:00:00 | 2011-01-02 | 03:00:00 | 2011 | 1 | 2 | 3 | 6 | 1.0 |
| 28 | 2011-01-02 04:00:00 | 2011-01-02 | 04:00:00 | 2011 | 1 | 2 | 4 | 6 | 1.0 |
| 29 | 2011-01-02 06:00:00 | 2011-01-02 | 06:00:00 | 2011 | 1 | 2 | 6 | 6 | 1.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 10856 | 2012-12-18 18:00:00 | 2012-12-18 | 18:00:00 | 2012 | 12 | 18 | 18 | 1 | 717.0 |
| 10857 | 2012-12-18 19:00:00 | 2012-12-18 | 19:00:00 | 2012 | 12 | 18 | 19 | 1 | 717.0 |
| 10858 | 2012-12-18 20:00:00 | 2012-12-18 | 20:00:00 | 2012 | 12 | 18 | 20 | 1 | 717.0 |
| 10859 | 2012-12-18 21:00:00 | 2012-12-18 | 21:00:00 | 2012 | 12 | 18 | 21 | 1 | 717.0 |
| 10860 | 2012-12-18 22:00:00 | 2012-12-18 | 22:00:00 | 2012 | 12 | 18 | 22 | 1 | 717.0 |
| 10861 | 2012-12-18 23:00:00 | 2012-12-18 | 23:00:00 | 2012 | 12 | 18 | 23 | 1 | 717.0 |
| 10862 | 2012-12-19 00:00:00 | 2012-12-19 | 00:00:00 | 2012 | 12 | 19 | 0 | 2 | 718.0 |
| 10863 | 2012-12-19 01:00:00 | 2012-12-19 | 01:00:00 | 2012 | 12 | 19 | 1 | 2 | 718.0 |
| 10864 | 2012-12-19 02:00:00 | 2012-12-19 | 02:00:00 | 2012 | 12 | 19 | 2 | 2 | 718.0 |
| 10865 | 2012-12-19 03:00:00 | 2012-12-19 | 03:00:00 | 2012 | 12 | 19 | 3 | 2 | 718.0 |
| 10866 | 2012-12-19 04:00:00 | 2012-12-19 | 04:00:00 | 2012 | 12 | 19 | 4 | 2 | 718.0 |
| 10867 | 2012-12-19 05:00:00 | 2012-12-19 | 05:00:00 | 2012 | 12 | 19 | 5 | 2 | 718.0 |
| 10868 | 2012-12-19 06:00:00 | 2012-12-19 | 06:00:00 | 2012 | 12 | 19 | 6 | 2 | 718.0 |
| 10869 | 2012-12-19 07:00:00 | 2012-12-19 | 07:00:00 | 2012 | 12 | 19 | 7 | 2 | 718.0 |
| 10870 | 2012-12-19 08:00:00 | 2012-12-19 | 08:00:00 | 2012 | 12 | 19 | 8 | 2 | 718.0 |
| 10871 | 2012-12-19 09:00:00 | 2012-12-19 | 09:00:00 | 2012 | 12 | 19 | 9 | 2 | 718.0 |
| 10872 | 2012-12-19 10:00:00 | 2012-12-19 | 10:00:00 | 2012 | 12 | 19 | 10 | 2 | 718.0 |
| 10873 | 2012-12-19 11:00:00 | 2012-12-19 | 11:00:00 | 2012 | 12 | 19 | 11 | 2 | 718.0 |
| 10874 | 2012-12-19 12:00:00 | 2012-12-19 | 12:00:00 | 2012 | 12 | 19 | 12 | 2 | 718.0 |
| 10875 | 2012-12-19 13:00:00 | 2012-12-19 | 13:00:00 | 2012 | 12 | 19 | 13 | 2 | 718.0 |
| 10876 | 2012-12-19 14:00:00 | 2012-12-19 | 14:00:00 | 2012 | 12 | 19 | 14 | 2 | 718.0 |
| 10877 | 2012-12-19 15:00:00 | 2012-12-19 | 15:00:00 | 2012 | 12 | 19 | 15 | 2 | 718.0 |
| 10878 | 2012-12-19 16:00:00 | 2012-12-19 | 16:00:00 | 2012 | 12 | 19 | 16 | 2 | 718.0 |
| 10879 | 2012-12-19 17:00:00 | 2012-12-19 | 17:00:00 | 2012 | 12 | 19 | 17 | 2 | 718.0 |
| 10880 | 2012-12-19 18:00:00 | 2012-12-19 | 18:00:00 | 2012 | 12 | 19 | 18 | 2 | 718.0 |
| 10881 | 2012-12-19 19:00:00 | 2012-12-19 | 19:00:00 | 2012 | 12 | 19 | 19 | 2 | 718.0 |
| 10882 | 2012-12-19 20:00:00 | 2012-12-19 | 20:00:00 | 2012 | 12 | 19 | 20 | 2 | 718.0 |
| 10883 | 2012-12-19 21:00:00 | 2012-12-19 | 21:00:00 | 2012 | 12 | 19 | 21 | 2 | 718.0 |
| 10884 | 2012-12-19 22:00:00 | 2012-12-19 | 22:00:00 | 2012 | 12 | 19 | 22 | 2 | 718.0 |
| 10885 | 2012-12-19 23:00:00 | 2012-12-19 | 23:00:00 | 2012 | 12 | 19 | 23 | 2 | 718.0 |
10886 rows × 9 columns
temp
DatetimeIndex(['2011-01-01 00:00:00', '2011-01-01 01:00:00',
'2011-01-01 02:00:00', '2011-01-01 03:00:00',
'2011-01-01 04:00:00', '2011-01-01 05:00:00',
'2011-01-01 06:00:00', '2011-01-01 07:00:00',
'2011-01-01 08:00:00', '2011-01-01 09:00:00',
...
'2012-12-19 14:00:00', '2012-12-19 15:00:00',
'2012-12-19 16:00:00', '2012-12-19 17:00:00',
'2012-12-19 18:00:00', '2012-12-19 19:00:00',
'2012-12-19 20:00:00', '2012-12-19 21:00:00',
'2012-12-19 22:00:00', '2012-12-19 23:00:00'],
dtype='datetime64[ns]', name='datetime', length=10886, freq=None)
3.3特征降维
在实际项目中,并不是维数越高越好,为什么要进行降维操作,主要是出于一下考虑
- 特征维数越高,模型越容易过拟合,此时更复杂的模型就不好用。
- 相互独立的特征维数越高,在模型不变的情况下,在测试集上达到相同的效果表现所需要的训练样本的数目就越大。
- 特征数量增加带来的训练、测试以及存储的开销都会增大。
- 在某些模型中,例如基于距离计算的模型KMeans,KNN等模型,在进行距离计算时,维度过高会影响精度和性能。5.可视化分析的需要。在低维的情况下,例如二维,三维,我们可以把数据绘制出来,可视化地看到数据。当维度增高时,就难以绘制出来了。
在机器学习中,有一个非常经典的维度灾难的概念。
正是由于高维特征有如上描述的各种各样的问题,所以我们需要进行特征降维和特征选择等工作。特征降维常用的算法有PCA,LDA等。特征降维的目标是将高维空间中的数据集映射到低维空间数据,同时尽可能少地丢失信息,或者降维后的数据点尽可能地容易被区分 关于PCA算法,在之前的文章有介绍 PCA算法分析
3.4 特征选择
当数据预处理完成后,我们需要选择有意义的特征输入机器学习的算法和模型进行训练。
特征选择的目标是寻找最优特征子集。特征选择能剔除不相关(irrelevant)或冗余(redundant )的特征,从而达到减少特征个数,提高模型精确度,减少运行时间的目的。另一方面,选取出真正相关的特征简化模型,协助理解数据产生的过程。
根据特征选项的形式,可以将特征选择方法分为三种
- Filter:过滤法,按照发散性或者相关性对各个特征进行评分,设定阈值或者待选择阈值的个数,排序留下Top 相关的特征部分。
- Wrapper:包装法,根据目标函数(通常是预测效果评分),每次选择若干特征,或者排除若干特征。
- Embedded:嵌入法,先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据系数从大到小选择特征。类似于Filter方法,但是是通过训练来确定特征的优劣。
3.4.1 Filter(过滤法)
方差选择法
使用方差选择法,先要计算各个特征的方差,然后根据阈值,选择方差大于阈值的特征。
from sklearn.feature_selection import VarianceThreshold
# iris.data[:,0].var() #0.6811222222222223
# iris.data[:,1].var() #0.18675066666666668
# iris.data[:,2].var() #3.092424888888889
# iris.data[:,3].var() #0.5785315555555555
#threshold:比较的方差的阈值,返回方差大于阈值的特征对应的数据。针对上面的鸢尾花数据集,只会返回第三列数据
# VarianceThreshold(threshold=3).fit_transform(iris.data)
相关系数法
使用相关系数法,先要计算各个特征对目标值的相关系数以及相关系数的P值。
用feature_selection库的SelectKBest类结合相关系数来选择特征的代码如下
#首先看下皮尔森相关系数的计算
from scipy.stats import pearsonr #用来计算相关系数
np.random.seed(0) #设置相同的seed,每次生成的随机数相同
size = 300
test = np.random.normal(0,1,size)
# print("加入低噪声后:",pearsonr(test,test+np.random.normal(0,1,size))) #返回的第一个值为相关系数,第二个值为P值
# print("加入高噪声后:",pearsonr(test,test+np.random.normal(0,10,size)))
#相关系统越高,p值越小
from sklearn.feature_selection import SelectKBest
#选择K个最好的特征,返回选择特征后的数据
#第一个参数为计算评估特征是否好的函数,该函数输入特征矩阵和目标向量,输出二元组(评分,P值)的数组,数组第i项为第i个特征的评分和P值。在此定义为计算相关系数
#参数k为选择的特征个数
SelectKBest(lambda X, Y: list(np.array(list(map(lambda x:pearsonr(x, Y), X.T))).T), k=2).fit_transform(iris.data, iris.target)
array([[1.4, 0.2],
[1.4, 0.2],
[1.3, 0.2],
[1.5, 0.2],
[1.4, 0.2],
[1.7, 0.4],
[1.4, 0.3],
[1.5, 0.2],
[1.4, 0.2],
[1.5, 0.1],
[1.5, 0.2],
[1.6, 0.2],
[1.4, 0.1],
[1.1, 0.1],
[1.2, 0.2],
[1.5, 0.4],
[1.3, 0.4],
[1.4, 0.3],
[1.7, 0.3],
[1.5, 0.3],
[1.7, 0.2],
[1.5, 0.4],
[1. , 0.2],
[1.7, 0.5],
[1.9, 0.2],
[1.6, 0.2],
[1.6, 0.4],
[1.5, 0.2],
[1.4, 0.2],
[1.6, 0.2],
[1.6, 0.2],
[1.5, 0.4],
[1.5, 0.1],
[1.4, 0.2],
[1.5, 0.1],
[1.2, 0.2],
[1.3, 0.2],
[1.5, 0.1],
[1.3, 0.2],
[1.5, 0.2],
[1.3, 0.3],
[1.3, 0.3],
[1.3, 0.2],
[1.6, 0.6],
[1.9, 0.4],
[1.4, 0.3],
[1.6, 0.2],
[1.4, 0.2],
[1.5, 0.2],
[1.4, 0.2],
[4.7, 1.4],
[4.5, 1.5],
[4.9, 1.5],
[4. , 1.3],
[4.6, 1.5],
[4.5, 1.3],
[4.7, 1.6],
[3.3, 1. ],
[4.6, 1.3],
[3.9, 1.4],
[3.5, 1. ],
[4.2, 1.5],
[4. , 1. ],
[4.7, 1.4],
[3.6, 1.3],
[4.4, 1.4],
[4.5, 1.5],
[4.1, 1. ],
[4.5, 1.5],
[3.9, 1.1],
[4.8, 1.8],
[4. , 1.3],
[4.9, 1.5],
[4.7, 1.2],
[4.3, 1.3],
[4.4, 1.4],
[4.8, 1.4],
[5. , 1.7],
[4.5, 1.5],
[3.5, 1. ],
[3.8, 1.1],
[3.7, 1. ],
[3.9, 1.2],
[5.1, 1.6],
[4.5, 1.5],
[4.5, 1.6],
[4.7, 1.5],
[4.4, 1.3],
[4.1, 1.3],
[4. , 1.3],
[4.4, 1.2],
[4.6, 1.4],
[4. , 1.2],
[3.3, 1. ],
[4.2, 1.3],
[4.2, 1.2],
[4.2, 1.3],
[4.3, 1.3],
[3. , 1.1],
[4.1, 1.3],
[6. , 2.5],
[5.1, 1.9],
[5.9, 2.1],
[5.6, 1.8],
[5.8, 2.2],
[6.6, 2.1],
[4.5, 1.7],
[6.3, 1.8],
[5.8, 1.8],
[6.1, 2.5],
[5.1, 2. ],
[5.3, 1.9],
[5.5, 2.1],
[5. , 2. ],
[5.1, 2.4],
[5.3, 2.3],
[5.5, 1.8],
[6.7, 2.2],
[6.9, 2.3],
[5. , 1.5],
[5.7, 2.3],
[4.9, 2. ],
[6.7, 2. ],
[4.9, 1.8],
[5.7, 2.1],
[6. , 1.8],
[4.8, 1.8],
[4.9, 1.8],
[5.6, 2.1],
[5.8, 1.6],
[6.1, 1.9],
[6.4, 2. ],
[5.6, 2.2],
[5.1, 1.5],
[5.6, 1.4],
[6.1, 2.3],
[5.6, 2.4],
[5.5, 1.8],
[4.8, 1.8],
[5.4, 2.1],
[5.6, 2.4],
[5.1, 2.3],
[5.1, 1.9],
[5.9, 2.3],
[5.7, 2.5],
[5.2, 2.3],
[5. , 1.9],
[5.2, 2. ],
[5.4, 2.3],
[5.1, 1.8]])
卡方检验
经典的卡方检验是检验定性自变量对定性因变量的相关性。假设自变量有N种取值,因变量有M种取值,考虑自变量等于i且因变量等于j的样本频数的观察值与期望的差距,构建统计量:
用feature_selection库的SelectKBest类结合卡方检验来选择特征的代码如下:
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
#选择K个最好的特征,返回选择特征后的数据
SelectKBest(chi2, k=2).fit_transform(iris.data, iris.target)
array([[1.4, 0.2],
[1.4, 0.2],
[1.3, 0.2],
[1.5, 0.2],
[1.4, 0.2],
[1.7, 0.4],
[1.4, 0.3],
[1.5, 0.2],
[1.4, 0.2],
[1.5, 0.1],
[1.5, 0.2],
[1.6, 0.2],
[1.4, 0.1],
[1.1, 0.1],
[1.2, 0.2],
[1.5, 0.4],
[1.3, 0.4],
[1.4, 0.3],
[1.7, 0.3],
[1.5, 0.3],
[1.7, 0.2],
[1.5, 0.4],
[1. , 0.2],
[1.7, 0.5],
[1.9, 0.2],
[1.6, 0.2],
[1.6, 0.4],
[1.5, 0.2],
[1.4, 0.2],
[1.6, 0.2],
[1.6, 0.2],
[1.5, 0.4],
[1.5, 0.1],
[1.4, 0.2],
[1.5, 0.1],
[1.2, 0.2],
[1.3, 0.2],
[1.5, 0.1],
[1.3, 0.2],
[1.5, 0.2],
[1.3, 0.3],
[1.3, 0.3],
[1.3, 0.2],
[1.6, 0.6],
[1.9, 0.4],
[1.4, 0.3],
[1.6, 0.2],
[1.4, 0.2],
[1.5, 0.2],
[1.4, 0.2],
[4.7, 1.4],
[4.5, 1.5],
[4.9, 1.5],
[4. , 1.3],
[4.6, 1.5],
[4.5, 1.3],
[4.7, 1.6],
[3.3, 1. ],
[4.6, 1.3],
[3.9, 1.4],
[3.5, 1. ],
[4.2, 1.5],
[4. , 1. ],
[4.7, 1.4],
[3.6, 1.3],
[4.4, 1.4],
[4.5, 1.5],
[4.1, 1. ],
[4.5, 1.5],
[3.9, 1.1],
[4.8, 1.8],
[4. , 1.3],
[4.9, 1.5],
[4.7, 1.2],
[4.3, 1.3],
[4.4, 1.4],
[4.8, 1.4],
[5. , 1.7],
[4.5, 1.5],
[3.5, 1. ],
[3.8, 1.1],
[3.7, 1. ],
[3.9, 1.2],
[5.1, 1.6],
[4.5, 1.5],
[4.5, 1.6],
[4.7, 1.5],
[4.4, 1.3],
[4.1, 1.3],
[4. , 1.3],
[4.4, 1.2],
[4.6, 1.4],
[4. , 1.2],
[3.3, 1. ],
[4.2, 1.3],
[4.2, 1.2],
[4.2, 1.3],
[4.3, 1.3],
[3. , 1.1],
[4.1, 1.3],
[6. , 2.5],
[5.1, 1.9],
[5.9, 2.1],
[5.6, 1.8],
[5.8, 2.2],
[6.6, 2.1],
[4.5, 1.7],
[6.3, 1.8],
[5.8, 1.8],
[6.1, 2.5],
[5.1, 2. ],
[5.3, 1.9],
[5.5, 2.1],
[5. , 2. ],
[5.1, 2.4],
[5.3, 2.3],
[5.5, 1.8],
[6.7, 2.2],
[6.9, 2.3],
[5. , 1.5],
[5.7, 2.3],
[4.9, 2. ],
[6.7, 2. ],
[4.9, 1.8],
[5.7, 2.1],
[6. , 1.8],
[4.8, 1.8],
[4.9, 1.8],
[5.6, 2.1],
[5.8, 1.6],
[6.1, 1.9],
[6.4, 2. ],
[5.6, 2.2],
[5.1, 1.5],
[5.6, 1.4],
[6.1, 2.3],
[5.6, 2.4],
[5.5, 1.8],
[4.8, 1.8],
[5.4, 2.1],
[5.6, 2.4],
[5.1, 2.3],
[5.1, 1.9],
[5.9, 2.3],
[5.7, 2.5],
[5.2, 2.3],
[5. , 1.9],
[5.2, 2. ],
[5.4, 2.3],
[5.1, 1.8]])
3.4.2 Wrapper(包裹型)
把特征选择看做一个特征子集搜索问题,筛选各种特 征子集,用模型评估效果。
典型的包裹型算法为 “递归特征删除算 法”
递归特征消除法
递归消除特征法使用一个基模型来进行多轮训练,每轮训练后,消除若干权值系数的特征,再基于新的特征集进行下一轮训练。
比如用逻辑回归,怎么做这个事情呢?
① 用全量特征跑一个模型
② 根据线性模型的系数(体现相关性),删掉5-10%的弱特征,观 察准确率/auc的变化
③ 逐步进行,直至准确率/auc出现大的下滑停止
from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression
#递归特征消除法,返回特征选择后的数据
#参数estimator为基模型
#参数n_features_to_select为选择的特征个数
RFE(estimator=LogisticRegression(), n_features_to_select=2).fit_transform(iris.data, iris.target)
array([[3.5, 0.2],
[3. , 0.2],
[3.2, 0.2],
[3.1, 0.2],
[3.6, 0.2],
[3.9, 0.4],
[3.4, 0.3],
[3.4, 0.2],
[2.9, 0.2],
[3.1, 0.1],
[3.7, 0.2],
[3.4, 0.2],
[3. , 0.1],
[3. , 0.1],
[4. , 0.2],
[4.4, 0.4],
[3.9, 0.4],
[3.5, 0.3],
[3.8, 0.3],
[3.8, 0.3],
[3.4, 0.2],
[3.7, 0.4],
[3.6, 0.2],
[3.3, 0.5],
[3.4, 0.2],
[3. , 0.2],
[3.4, 0.4],
[3.5, 0.2],
[3.4, 0.2],
[3.2, 0.2],
[3.1, 0.2],
[3.4, 0.4],
[4.1, 0.1],
[4.2, 0.2],
[3.1, 0.1],
[3.2, 0.2],
[3.5, 0.2],
[3.1, 0.1],
[3. , 0.2],
[3.4, 0.2],
[3.5, 0.3],
[2.3, 0.3],
[3.2, 0.2],
[3.5, 0.6],
[3.8, 0.4],
[3. , 0.3],
[3.8, 0.2],
[3.2, 0.2],
[3.7, 0.2],
[3.3, 0.2],
[3.2, 1.4],
[3.2, 1.5],
[3.1, 1.5],
[2.3, 1.3],
[2.8, 1.5],
[2.8, 1.3],
[3.3, 1.6],
[2.4, 1. ],
[2.9, 1.3],
[2.7, 1.4],
[2. , 1. ],
[3. , 1.5],
[2.2, 1. ],
[2.9, 1.4],
[2.9, 1.3],
[3.1, 1.4],
[3. , 1.5],
[2.7, 1. ],
[2.2, 1.5],
[2.5, 1.1],
[3.2, 1.8],
[2.8, 1.3],
[2.5, 1.5],
[2.8, 1.2],
[2.9, 1.3],
[3. , 1.4],
[2.8, 1.4],
[3. , 1.7],
[2.9, 1.5],
[2.6, 1. ],
[2.4, 1.1],
[2.4, 1. ],
[2.7, 1.2],
[2.7, 1.6],
[3. , 1.5],
[3.4, 1.6],
[3.1, 1.5],
[2.3, 1.3],
[3. , 1.3],
[2.5, 1.3],
[2.6, 1.2],
[3. , 1.4],
[2.6, 1.2],
[2.3, 1. ],
[2.7, 1.3],
[3. , 1.2],
[2.9, 1.3],
[2.9, 1.3],
[2.5, 1.1],
[2.8, 1.3],
[3.3, 2.5],
[2.7, 1.9],
[3. , 2.1],
[2.9, 1.8],
[3. , 2.2],
[3. , 2.1],
[2.5, 1.7],
[2.9, 1.8],
[2.5, 1.8],
[3.6, 2.5],
[3.2, 2. ],
[2.7, 1.9],
[3. , 2.1],
[2.5, 2. ],
[2.8, 2.4],
[3.2, 2.3],
[3. , 1.8],
[3.8, 2.2],
[2.6, 2.3],
[2.2, 1.5],
[3.2, 2.3],
[2.8, 2. ],
[2.8, 2. ],
[2.7, 1.8],
[3.3, 2.1],
[3.2, 1.8],
[2.8, 1.8],
[3. , 1.8],
[2.8, 2.1],
[3. , 1.6],
[2.8, 1.9],
[3.8, 2. ],
[2.8, 2.2],
[2.8, 1.5],
[2.6, 1.4],
[3. , 2.3],
[3.4, 2.4],
[3.1, 1.8],
[3. , 1.8],
[3.1, 2.1],
[3.1, 2.4],
[3.1, 2.3],
[2.7, 1.9],
[3.2, 2.3],
[3.3, 2.5],
[3. , 2.3],
[2.5, 1.9],
[3. , 2. ],
[3.4, 2.3],
[3. , 1.8]])
3.4.3 Embedded(嵌入型)
基于惩罚项的特征选择法
使用带惩罚项的基模型,除了筛选出特征外,同时也进行了降维。使用feature_selection库的SelectFromModel类结合带L1惩罚项的逻辑回归模型,来选择特征的代码如下:
from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression
#带L1惩罚项的逻辑回归作为基模型的特征选择
SelectFromModel(LogisticRegression(penalty="l1", C=0.1)).fit_transform(iris.data, iris.target)
array([[5.1, 3.5, 1.4],
[4.9, 3. , 1.4],
[4.7, 3.2, 1.3],
[4.6, 3.1, 1.5],
[5. , 3.6, 1.4],
[5.4, 3.9, 1.7],
[4.6, 3.4, 1.4],
[5. , 3.4, 1.5],
[4.4, 2.9, 1.4],
[4.9, 3.1, 1.5],
[5.4, 3.7, 1.5],
[4.8, 3.4, 1.6],
[4.8, 3. , 1.4],
[4.3, 3. , 1.1],
[5.8, 4. , 1.2],
[5.7, 4.4, 1.5],
[5.4, 3.9, 1.3],
[5.1, 3.5, 1.4],
[5.7, 3.8, 1.7],
[5.1, 3.8, 1.5],
[5.4, 3.4, 1.7],
[5.1, 3.7, 1.5],
[4.6, 3.6, 1. ],
[5.1, 3.3, 1.7],
[4.8, 3.4, 1.9],
[5. , 3. , 1.6],
[5. , 3.4, 1.6],
[5.2, 3.5, 1.5],
[5.2, 3.4, 1.4],
[4.7, 3.2, 1.6],
[4.8, 3.1, 1.6],
[5.4, 3.4, 1.5],
[5.2, 4.1, 1.5],
[5.5, 4.2, 1.4],
[4.9, 3.1, 1.5],
[5. , 3.2, 1.2],
[5.5, 3.5, 1.3],
[4.9, 3.1, 1.5],
[4.4, 3. , 1.3],
[5.1, 3.4, 1.5],
[5. , 3.5, 1.3],
[4.5, 2.3, 1.3],
[4.4, 3.2, 1.3],
[5. , 3.5, 1.6],
[5.1, 3.8, 1.9],
[4.8, 3. , 1.4],
[5.1, 3.8, 1.6],
[4.6, 3.2, 1.4],
[5.3, 3.7, 1.5],
[5. , 3.3, 1.4],
[7. , 3.2, 4.7],
[6.4, 3.2, 4.5],
[6.9, 3.1, 4.9],
[5.5, 2.3, 4. ],
[6.5, 2.8, 4.6],
[5.7, 2.8, 4.5],
[6.3, 3.3, 4.7],
[4.9, 2.4, 3.3],
[6.6, 2.9, 4.6],
[5.2, 2.7, 3.9],
[5. , 2. , 3.5],
[5.9, 3. , 4.2],
[6. , 2.2, 4. ],
[6.1, 2.9, 4.7],
[5.6, 2.9, 3.6],
[6.7, 3.1, 4.4],
[5.6, 3. , 4.5],
[5.8, 2.7, 4.1],
[6.2, 2.2, 4.5],
[5.6, 2.5, 3.9],
[5.9, 3.2, 4.8],
[6.1, 2.8, 4. ],
[6.3, 2.5, 4.9],
[6.1, 2.8, 4.7],
[6.4, 2.9, 4.3],
[6.6, 3. , 4.4],
[6.8, 2.8, 4.8],
[6.7, 3. , 5. ],
[6. , 2.9, 4.5],
[5.7, 2.6, 3.5],
[5.5, 2.4, 3.8],
[5.5, 2.4, 3.7],
[5.8, 2.7, 3.9],
[6. , 2.7, 5.1],
[5.4, 3. , 4.5],
[6. , 3.4, 4.5],
[6.7, 3.1, 4.7],
[6.3, 2.3, 4.4],
[5.6, 3. , 4.1],
[5.5, 2.5, 4. ],
[5.5, 2.6, 4.4],
[6.1, 3. , 4.6],
[5.8, 2.6, 4. ],
[5. , 2.3, 3.3],
[5.6, 2.7, 4.2],
[5.7, 3. , 4.2],
[5.7, 2.9, 4.2],
[6.2, 2.9, 4.3],
[5.1, 2.5, 3. ],
[5.7, 2.8, 4.1],
[6.3, 3.3, 6. ],
[5.8, 2.7, 5.1],
[7.1, 3. , 5.9],
[6.3, 2.9, 5.6],
[6.5, 3. , 5.8],
[7.6, 3. , 6.6],
[4.9, 2.5, 4.5],
[7.3, 2.9, 6.3],
[6.7, 2.5, 5.8],
[7.2, 3.6, 6.1],
[6.5, 3.2, 5.1],
[6.4, 2.7, 5.3],
[6.8, 3. , 5.5],
[5.7, 2.5, 5. ],
[5.8, 2.8, 5.1],
[6.4, 3.2, 5.3],
[6.5, 3. , 5.5],
[7.7, 3.8, 6.7],
[7.7, 2.6, 6.9],
[6. , 2.2, 5. ],
[6.9, 3.2, 5.7],
[5.6, 2.8, 4.9],
[7.7, 2.8, 6.7],
[6.3, 2.7, 4.9],
[6.7, 3.3, 5.7],
[7.2, 3.2, 6. ],
[6.2, 2.8, 4.8],
[6.1, 3. , 4.9],
[6.4, 2.8, 5.6],
[7.2, 3. , 5.8],
[7.4, 2.8, 6.1],
[7.9, 3.8, 6.4],
[6.4, 2.8, 5.6],
[6.3, 2.8, 5.1],
[6.1, 2.6, 5.6],
[7.7, 3. , 6.1],
[6.3, 3.4, 5.6],
[6.4, 3.1, 5.5],
[6. , 3. , 4.8],
[6.9, 3.1, 5.4],
[6.7, 3.1, 5.6],
[6.9, 3.1, 5.1],
[5.8, 2.7, 5.1],
[6.8, 3.2, 5.9],
[6.7, 3.3, 5.7],
[6.7, 3. , 5.2],
[6.3, 2.5, 5. ],
[6.5, 3. , 5.2],
[6.2, 3.4, 5.4],
[5.9, 3. , 5.1]])
基于树模型的特征选择法
树模型中GBDT也可用来作为基模型进行特征选择,使用feature_selection库的SelectFromModel类结合GBDT模型,来选择特征的代码如下
from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import GradientBoostingClassifier
#GBDT作为基模型的特征选择
SelectFromModel(GradientBoostingClassifier()).fit_transform(iris.data, iris.target)
array([[1.4, 0.2],
[1.4, 0.2],
[1.3, 0.2],
[1.5, 0.2],
[1.4, 0.2],
[1.7, 0.4],
[1.4, 0.3],
[1.5, 0.2],
[1.4, 0.2],
[1.5, 0.1],
[1.5, 0.2],
[1.6, 0.2],
[1.4, 0.1],
[1.1, 0.1],
[1.2, 0.2],
[1.5, 0.4],
[1.3, 0.4],
[1.4, 0.3],
[1.7, 0.3],
[1.5, 0.3],
[1.7, 0.2],
[1.5, 0.4],
[1. , 0.2],
[1.7, 0.5],
[1.9, 0.2],
[1.6, 0.2],
[1.6, 0.4],
[1.5, 0.2],
[1.4, 0.2],
[1.6, 0.2],
[1.6, 0.2],
[1.5, 0.4],
[1.5, 0.1],
[1.4, 0.2],
[1.5, 0.1],
[1.2, 0.2],
[1.3, 0.2],
[1.5, 0.1],
[1.3, 0.2],
[1.5, 0.2],
[1.3, 0.3],
[1.3, 0.3],
[1.3, 0.2],
[1.6, 0.6],
[1.9, 0.4],
[1.4, 0.3],
[1.6, 0.2],
[1.4, 0.2],
[1.5, 0.2],
[1.4, 0.2],
[4.7, 1.4],
[4.5, 1.5],
[4.9, 1.5],
[4. , 1.3],
[4.6, 1.5],
[4.5, 1.3],
[4.7, 1.6],
[3.3, 1. ],
[4.6, 1.3],
[3.9, 1.4],
[3.5, 1. ],
[4.2, 1.5],
[4. , 1. ],
[4.7, 1.4],
[3.6, 1.3],
[4.4, 1.4],
[4.5, 1.5],
[4.1, 1. ],
[4.5, 1.5],
[3.9, 1.1],
[4.8, 1.8],
[4. , 1.3],
[4.9, 1.5],
[4.7, 1.2],
[4.3, 1.3],
[4.4, 1.4],
[4.8, 1.4],
[5. , 1.7],
[4.5, 1.5],
[3.5, 1. ],
[3.8, 1.1],
[3.7, 1. ],
[3.9, 1.2],
[5.1, 1.6],
[4.5, 1.5],
[4.5, 1.6],
[4.7, 1.5],
[4.4, 1.3],
[4.1, 1.3],
[4. , 1.3],
[4.4, 1.2],
[4.6, 1.4],
[4. , 1.2],
[3.3, 1. ],
[4.2, 1.3],
[4.2, 1.2],
[4.2, 1.3],
[4.3, 1.3],
[3. , 1.1],
[4.1, 1.3],
[6. , 2.5],
[5.1, 1.9],
[5.9, 2.1],
[5.6, 1.8],
[5.8, 2.2],
[6.6, 2.1],
[4.5, 1.7],
[6.3, 1.8],
[5.8, 1.8],
[6.1, 2.5],
[5.1, 2. ],
[5.3, 1.9],
[5.5, 2.1],
[5. , 2. ],
[5.1, 2.4],
[5.3, 2.3],
[5.5, 1.8],
[6.7, 2.2],
[6.9, 2.3],
[5. , 1.5],
[5.7, 2.3],
[4.9, 2. ],
[6.7, 2. ],
[4.9, 1.8],
[5.7, 2.1],
[6. , 1.8],
[4.8, 1.8],
[4.9, 1.8],
[5.6, 2.1],
[5.8, 1.6],
[6.1, 1.9],
[6.4, 2. ],
[5.6, 2.2],
[5.1, 1.5],
[5.6, 1.4],
[6.1, 2.3],
[5.6, 2.4],
[5.5, 1.8],
[4.8, 1.8],
[5.4, 2.1],
[5.6, 2.4],
[5.1, 2.3],
[5.1, 1.9],
[5.9, 2.3],
[5.7, 2.5],
[5.2, 2.3],
[5. , 1.9],
[5.2, 2. ],
[5.4, 2.3],
[5.1, 1.8]])
上述就是关于特征工程的相关说明,至于特征监控相关的内容,目前还没了解过,等后面学习了再进行补充。
再进行完特征工程后,下一步需要做的就是模型选择与调优,下篇文章将主要学习整理这方面的知识
参考文章:
1.blog.csdn.net/rosenor1/ar…
2.www.cnblogs.com/jasonfreak/…
欢迎关注我的个人公众号 AI计算机视觉工坊,本公众号不定期推送机器学习,深度学习,计算机视觉等相关文章,欢迎大家和我一起学习,交流。
