起源
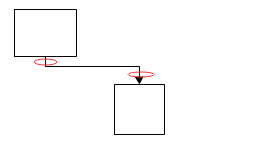
要用svg做一个流程图类似visio的连线,如下图的
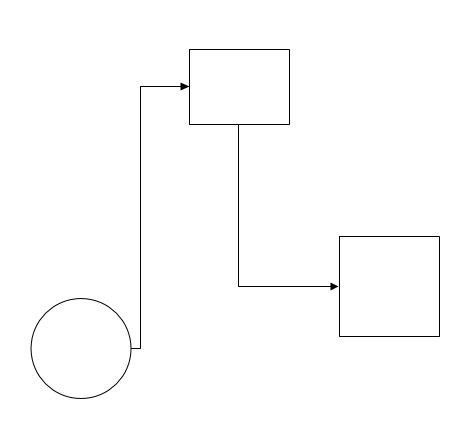
其实有很多库已经实现了流程图,比如 jointjs,gojs,jsplumb 等等。可惜都不是免费的。
分析
如果要做的简单呢,就用贝塞尔曲线就好了,只需要提供起点终点两个点的坐标,就能用简单的算法生成一个svg 的path了。这样算法网上应该找得到。
但是如果要用正交连线来实现,这个复杂度就上升了几个档次。我们来看看正交连线的多个情况:
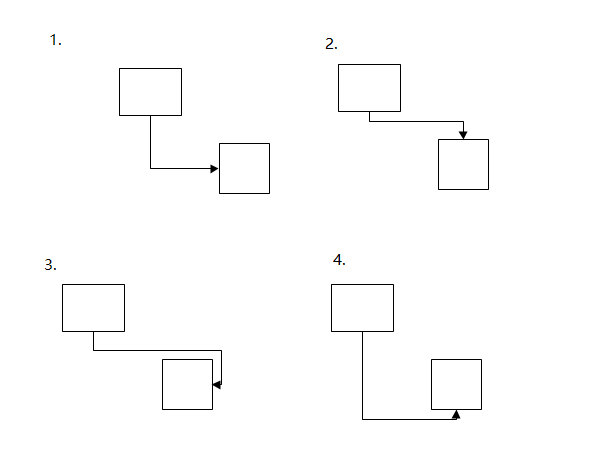
假设起点往下,目标节点在起始节点的右下方,那么可能存在的情况一共有四种。考虑到目标节点相对起始节点的方位有四种可能,那么所有连线的可能有4*4=16 种,再考虑到起点出发方向也有四种,那么所有的可能性有16 *4 = 64种。也就是说,如果你要用if else 来写,需要写64个分支。
怎么办
当然不必写64个if else ,写程序不就是要抽象出规律嘛! 将这个连线分成这么几个部分:
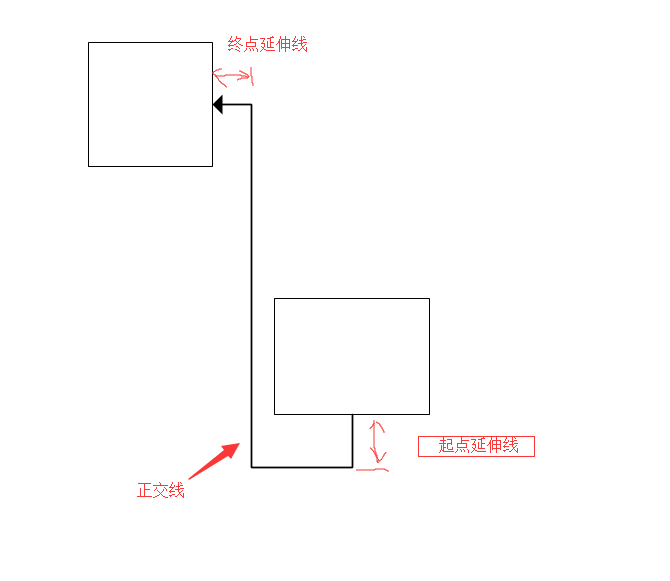
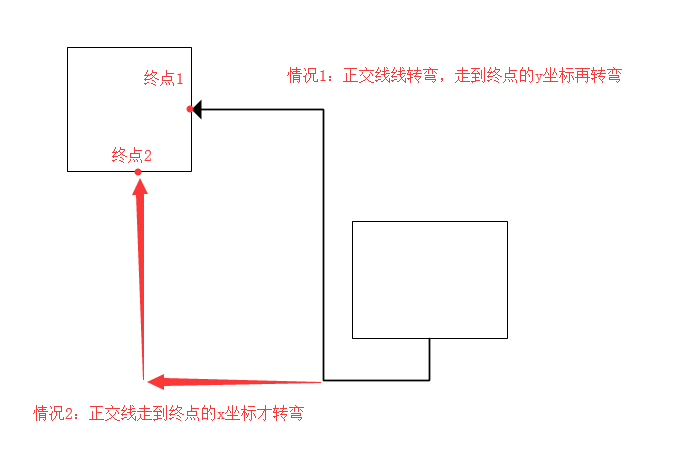
但是,我用了十八牛二虎之力找到了它的规律。
真相
这个连线的最终走向与这几个条件有关:
- 起点的出发方向
- 终点的进入方向
- 终点相对于起点的方向
- 起点开始的最小延伸线
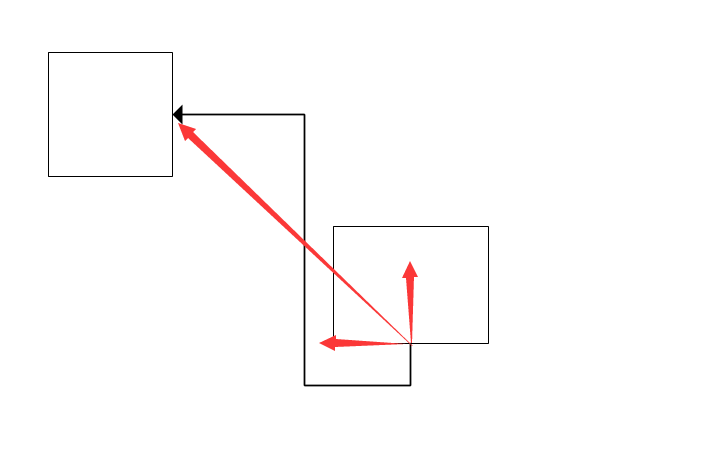
- 终点进入前的最小延伸线 (看下图)
实现思路
- 因为使用svg 的path 来画正交线。核心点是要找到转折点的坐标(其实用什么都一样)。
- 先获取起点到终点的向量(下文称为直接向量),以及两个正交向量(下文称为 直接向量的水平向量和竖直向量)
判断平行: x0 * y1-x1 * y0 === 0;
判断是否同公式,向量夹角为0度,则向量点积为1:x0 * y0 + x1 * y1 === 1
- 然后要获取正交线的最终方向。也是一样的思路,如果终点的进入方向与直接方向相反则取垂直方向,如果相同则取同向
- 得到了正交线起始方向和最终方向,现在需要获取正交线中间转弯的情况。判断这正交线起始方向和最终方向是否同向,如果同向,则需要转两个弯,如果不是同向,则只需转一个弯。
如果 正交线起始方向 == 正交线最终方向
那么 转弯数 = 2
否则 转弯数 = 1
- 如果转一个弯,那么获取转弯的坐标点
转弯的坐标点 = 正交线的第一个点 + 正交线起始方向向量
如果转两个弯,先获取第一个转弯点,既正交线始末方向的中点
第一个转弯点= 正交线的第一个点 + 正交线起始方向向量 * 0.5
再获取第二个转弯点 ,
非起始方向向量 = 从直接向量的水平向量和竖直向量 中取出与起始方向向量垂直的那个向量
第二个转弯点 = 第一个转弯点 + 非起始方向向量
- 最终生成所有点的坐标集合
所有点的坐标集合 = [起点,正交线的起点,...正交线的转弯点,正交线的终点,终点]
总结
这个算法的计算量不是很大,性能ok,适合边拖曳边重绘。但不是寻路算法,意味着没有避让节点的功能。
下一步要用曼哈顿算法来做一个。
这个demo拿去玩
desdesdesgo.github.io/flow-connec…
生成点的算法 github.com/Desdesdesgo…