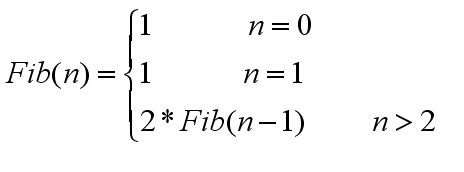在邓俊辉的数据结构教材的1.4节中简要介绍了一下递归问题,在查阅相关资料后,发现递归问题包含了以下几个方面:
- 线性递归(减而治之)
- 二分递归(分而治之)
- 动态规划问题
接下来结合教材以及网上相关资料对递归以及动态规划问题做一个简单的肤浅的入门的总结。
1.线性递归
线性递归(linear recursion)即减而治之(decrease-and-conquer)的思想:递归每深入一层,待求解问题的规模都缩减一个常数,直至最终蜕化为平凡的小(简单)问题。将一个规模为n的大问题退化为一个规模为n-1的小问题,直至退化为规模为1的平凡情况,这种情况称之为递归基(base case of recursion)。
比如如下教材中对数组求和的代码,若n=0则总和必为0(这也是最终的平凡情况,递归基);否则一般的,总和可理解为前n-1个整数(A[0,-1))之和,再加上末尾元素A[n-1]。
int sum(int A[], int n) { //数组求和算法(线性递归版)
if (1 > n) //平凡情况,递归基
return 0; //直接(非递归式)计算
else //一般情况
return sum(A, n - 1) + A[n - 1]; //递归:前n - 1向之和,再累计第n - 1项
} //O(n)
又比如下面的数组倒置问题,也就是将数组中各元素的次选前后翻转。借助线性递归不难解决这一问题,为此只需注意到并利用如下事实:为得到整个数组的倒置,可以先对换其首、末元素,然后递归地倒置除这两个元素以外的部分。
void reverse(int* A, int lo, int hi) { //数组倒置(多递归基线性递归版)
if (lo < hi) {
swap(A[lo], A[hi]); //交换A[lo]和A[hi]
reverse(A, lo + 1, hi - 1); //递归倒置A(lo, hi)
} //else隐含了两递归基
} //O(hi - lo + 1)
2.二分递归
二分递归(binary recursion)即分而治之(divide-and-conquer)的思想:将其分解为若干规模更小的子问题, 再通过递归机制分别求解。 这种分解持续进行,直到子问题规模缩减至平凡情况。在这种情况下,每一递归实例会调用多个递归来完成,故称作多路递归(multi-way recursion),通常都是将原问题一分为二,故有二分递归。
以下代码是对数组求和的二分递归的实现,新算法的思路是:以居中的元素为界将数组一分为二;递归地对子数组分别求和;最后,子数组之和相加即为原数组的总和。
int sum(int A[], int lo, int hi) { //数组求和算法(二分递归版,入口为sum(A, 0, n - 1))
if (lo == hi) //如遇递归基(区间长度已降至1),则
return A[lo]; //直接返回元素
else { //否则(一般情况下lo < hi),则
int mi = (lo + hi) >> 1; //以居中单元为界,将原区间间一分为二
return sum(A, lo, mi) + sum(A, mi + 1, hi); //递归对各子数组求和,然后合计
}
} //O(hi - lo + 1),线性正比与区间的长度
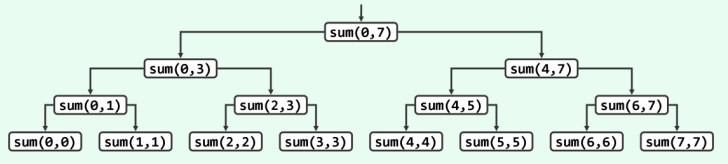
二分递归的效率问题 以下引用来自邓俊辉数据结构教材1.4节P24
当然,并非所有问题都适宜于采用分治策略。实际上除了递归,此类算法的计算消耗主要来自两个方面。首先是
子问题划分,即把原问题分解为形式相同、规模更小的多个子问题,比如sum()算法将待求和数组分为前、后两段。其次是子解答合并,即由递归所得子问题的解,得到原问题的整体解,比如由子数组之和累加得到整个数组之和。 为使分治策略真正有效, 不仅必须保证以上两方面的计算都能高效地实现, 还必须保证子问题之间相互独立———— 各子问题可独立求解, 而无需借助其它子问题的原始数据或中间结果。否则,或者子问题之间必须传递数据,或者子问题之间需要相互调用,无论如何都会导致时间和空间复 杂度的无谓增加。 以下就以Fibonacci数列的计算为例说明这一点。
Fibonacci数列定于如下:
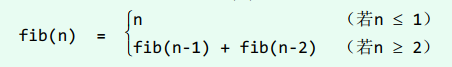
int fib(int n) { //计算Fibonacci数列列第n项(二分递归版): O(2^n)
//若达到递归基,直接取值,否则,递归计算前两项,其和即为正解
return (2 > n) ? n : fib(n - 1) + fib(n - 2);
}
基于Fibonacci数列原始定义的这一算法实现,不仅正确性一目了然,而且简洁自然。然而不幸的是,在这种场合采用二分递归策略的效率极其低下。实际上,该算法需要运行O(2^n)时间才能计算出第n个Fibonacci数。这一指数复杂度的算法,在实际环境中毫无价值。
对于Fibonacci问题最简单的实现就是迭代循环,也是一种比较直观的算法,g为当前项的值,f为前一项的值,从0开始往前计算直到返回欲求的第n项的数值。
int fibI(int n) { //计算Fibonacci数列的第n项(迭代版): O(n)
int f = 0, g = 1; //初始化: fib(0) = 0, fib(1) = 1
while (0 < n--) { g += f; f = g - f; } //依据原始定义,通过n次加法和减法计算fib(n)
return f; //迒回
}
3.动态规划
以下内容主要来自CSDN博客-HankingHu

A : "1+1+1+1+1+1+1+1 =?"
A : "上面等式的值是多少"
B : *计算* "8!"
A *在上面等式的左边写上 "1+" *
A : "此时等式的值为多少"
B : *quickly* "9!"
A : "你怎么这么快就知道答案了"
A : "只要在8的基础上加1就行了"
A : "所以你不用重新计算因为你记住了第一个等式的值为8!动态规划算法也可以说是 '记住求过的解来节省时间'"
由上面的图片和小故事可以知道动态规划算法的核心就是记住已经解决过的子问题的解。
动态规划算法的两种形式
上面已经知道动态规划算法的核心是记住已经求过的解,记住求解的方式有两种:①自顶向下的备忘录法 ②自底向上。为了说明动态规划的这两种方法,举一个最简单的例子:求斐波拉契数列Fibonacci 。
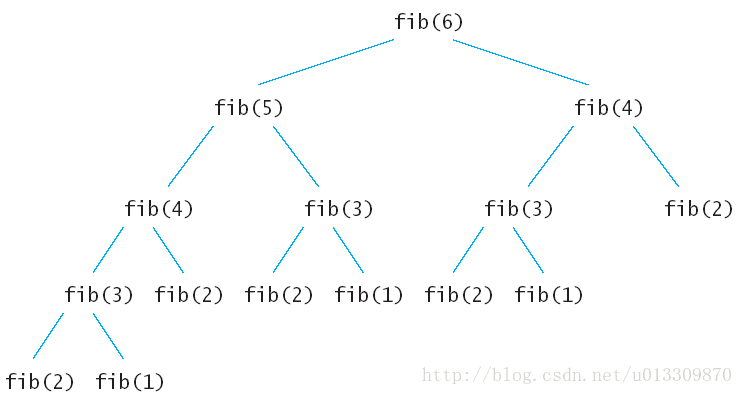
递归版本的Fibonacci算法在上面已经有了,此处不再重复。其执行的递归树如下图:
1.自顶向下的备忘录法
public static int Fibonacci(int n)
{
if(n<=0)
return n;
int []Memo=new int[n+1]; //备忘录数组
for(int i=0;i<=n;i++)
Memo[i]=-1;
return fib(n, Memo);
}
public static int fib(int n,int []Memo)
{
//如果已经求出了fib(n)的值直接返回,否则将求出的值保存在Memo备忘录中。
if(Memo[n]!=-1) return Memo[n];
if(n<=2) Memo[n]=1;
else Memo[n]=fib( n-1,Memo)+fib(n-2,Memo);
return Memo[n];
}
备忘录法也是比较好理解的,创建了一个n+1大小的数组来保存求出的斐波拉契数列中的每一个值,在递归的时候如果发现前面fib(n)的值计算出来了就不再计算,如果未计算出来,则计算出来后保存在Memo数组中,下次在调用fib(n)的时候就不会重新递归了。比如上面的递归树中在计算fib(6)的时候先计算fib(5),调用fib(5)算出了fib(4)后,fib(6)再调用fib(4)就不会再递归fib(4)的子树了,因为fib(4)的值已经保存在Memo[4]中。
2.自底向上的动态规划
备忘录法还是利用了递归,上面算法不管怎样,计算fib(6)的时候最后还是要计算出fib(1)、fib(2)、fib(3)……,那么何不先计算出fib(1)、fib(2)、fib(3)……,呢?这也就是动态规划的核心,先计算子问题,再由子问题计算父问题。
public static int fib(int n)
{
if(n<=0)
return n;
int []Memo=new int[n+1];
Memo[0]=0;
Memo[1]=1;
for(int i=2;i<=n;i++)
{
Memo[i]=Memo[i-1]+Memo[i-2];
}
return Memo[n];
}
自底向上方法也是利用数组保存了先计算的值,为后面的调用服务。观察参与循环的只有i,i-1,i-2三项,因此该方法的空间可以进一步的压缩如下。
public static int fib(int n)
{
if(n<=1)
return n;
int Memo_i_2=0;
int Memo_i_1=1;
int Memo_i=1;
for(int i=2;i<=n;i++)
{
Memo_i=Memo_i_2+Memo_i_1;
Memo_i_2=Memo_i_1;
Memo_i_1=Memo_i;
}
return Memo_i;
}
一般来说由于备忘录方式的动态规划方法使用了递归,递归的时候会产生额外的开销,使用自底向上的动态规划方法要比备忘录方法好。
4.跳台阶问题
跳台阶问题是典型的Fibonacci问题,有以下两种版本,以下内容主要来自hackbuteer1的CSDN博客:程序员面试100题之二:跳台阶问题(变态跳台阶)。
题目1:一个台阶总共有n级,如果一次可以跳1级,也可以跳2级。求总共有多少总跳法,并分析算法的时间复杂度。
分析:
这道题最近经常出现,包括MicroStrategy等比较重视算法的公司都曾先后选用过个这道题作为面试题或者笔试题。 首先我们考虑最简单的情况。如果只有1级台阶,那显然只有一种跳法。如果有2级台阶,那就有两种跳的方法了:一种是分两次跳,每次跳1级;另外一种就是一次跳2级。 现在我们再来讨论一般情况。我们把n级台阶时的跳法看成是n的函数,记为f(n)。当n>2时,第一次跳的时候就有两种不同的选择:一是第一次只跳1级,此时跳法数目等于后面剩下的n-1级台阶的跳法数目,即为f(n-1);另外一种选择是第一次跳2级,此时跳法数目等于后面剩下的n-2级台阶的跳法数目,即为f(n-2)。因此n级台阶时的不同跳法的总数f(n)=f(n-1)+(f-2)。我们把上面的分析用一个公式总结如下:
分析到这里,相信很多人都能看出这就是我们熟悉的Fibonacci序列。
题目2:一个台阶总共有n级,如果一次可以跳1级,也可以跳2级......它也可以跳上n级。此时该青蛙跳上一个n级的台阶总共有多少种跳法?
分析:
用Fib(n)表示青蛙跳上n阶台阶的跳法数,青蛙一次性跳上n阶台阶的跳法数1(n阶跳),设定Fib(0) = 1;
- 当n = 1 时, 只有一种跳法,即1阶跳:Fib(1) = 1;
- 当n = 2 时, 有两种跳的方式,一阶跳和二阶跳:Fib(2) = Fib(1) + Fib(0) = 2;
- 当n = 3 时,有三种跳的方式,第一次跳出一阶后,后面还有Fib(3-1)中跳法; 第一次跳出二阶后,后面还有Fib(3-2)中跳法;第一次跳出三阶后,后面还有Fib(3-3)中跳法
- 总计:
Fib(3) = Fib(2) + Fib(1)+Fib(0)=4;
当n = n 时,共有n种跳的方式:
- 第一次跳出一阶后,后面还有Fib(n-1)中跳法;
- 第一次跳出二阶后,后面还有Fib(n-2)中跳法;
- ……
- 第一次跳出n阶后,后面还有 Fib(n-n)中跳法.
- 总计:
Fib(n) = Fib(n-1)+Fib(n-2)+Fib(n-3)+...+Fib(n-n)=Fib(0)+Fib(1)+Fib(2)+...+Fib(n-1)- 又因为
Fib(n-1)=Fib(0)+Fib(1)+Fib(2)+...+Fib(n-2);- 两式相减得:
Fib(n)-Fib(n-1)=Fib(n-1)===== 》Fib(n) = 2*Fib(n-1); 递归等式如下:
5.总结及后续
HankingHu的博客在最后用一个切钢条的例子对动态规划做了更加详细的说明,但本文不再继续介绍了。因为本文主要是数据结构教材中递归(线性递归、二分递归)部分的简要总结,然后对Fibonacci的典型应用-跳台阶问题进行了介绍。关于动态规划的问题留待以后完善和总结。 博客对动态规划总结的很好,以后应该深入学习一下动态规划。