《The Book Of Shader》笔记,有增删。
一、随机(random)
说到随机函数,JavaScript 中有 Math.random(),PHP 中有rand(),在图形绘制时,随机也无处不在。《The Book Of Shader》 通过一个简单的函数衍化,让我们了解随机:
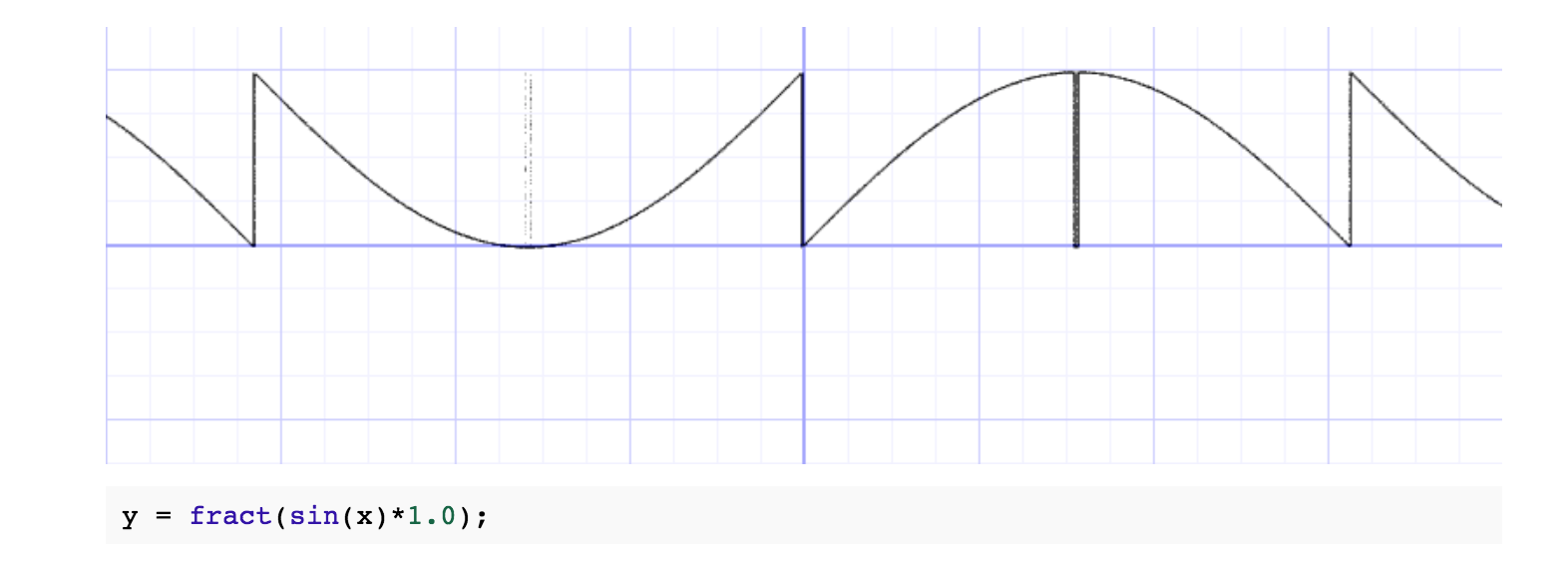
通过fract()和sin()的结合,我们得到了一个有一定规律但被打乱的曲线,当我们把1.0变成无限大时,再看看效果:
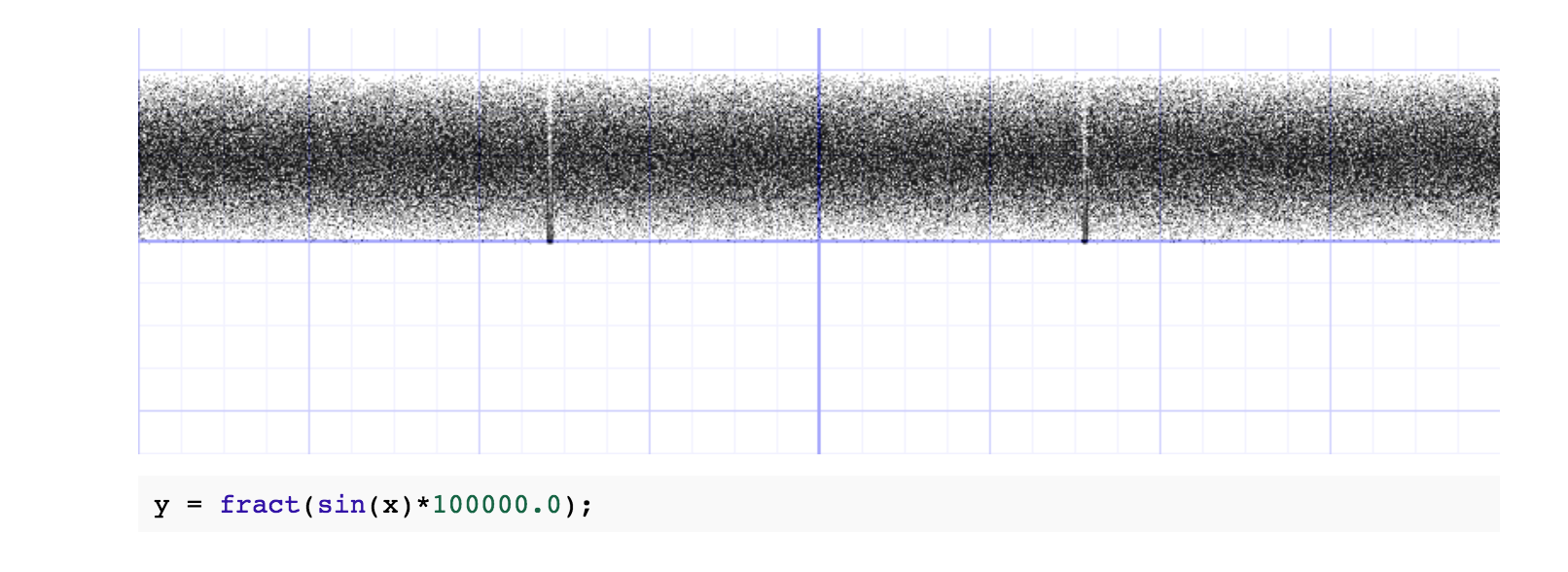
我们把上面的公式封装成rand()函数:
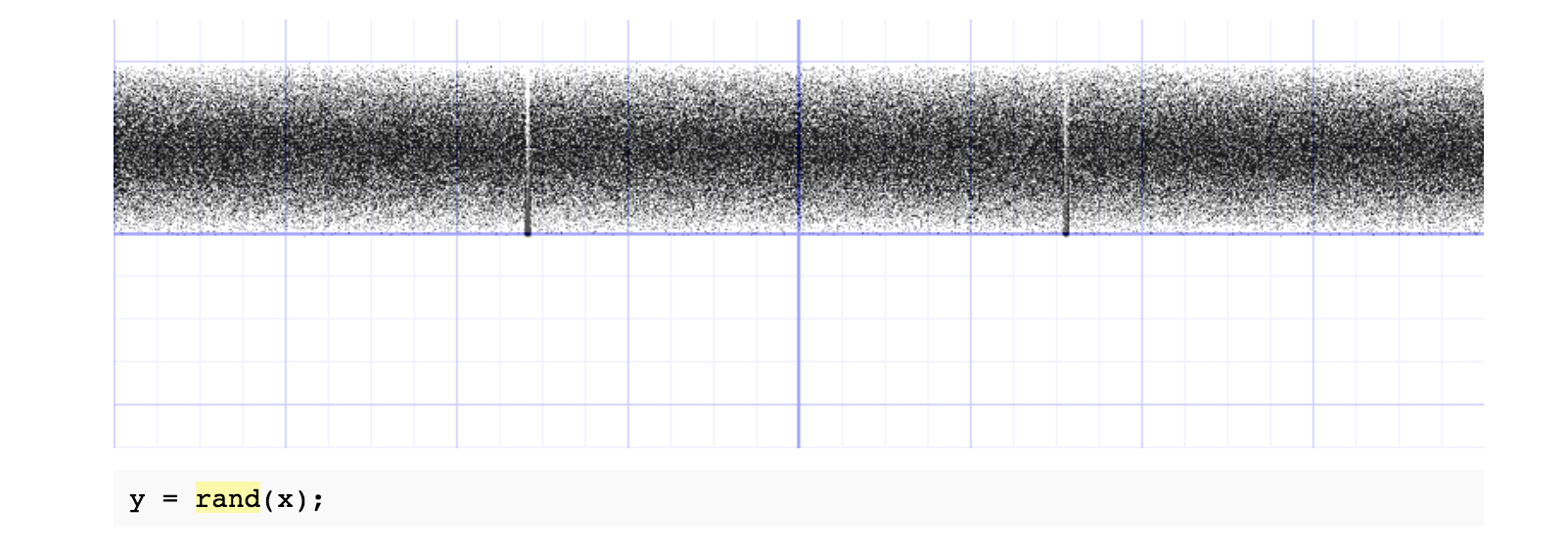
Shader 中的随机是确定性随机(伪随机),也就是当我们的输入值确定时,输出值也是确定的,而 JavaScript 和 PHP 则是非确定随机,每次随机出来的内容是不一样的。当然我们还可以对随机增加一些变化:
rand()*rand() 会让值更趋近于 0:
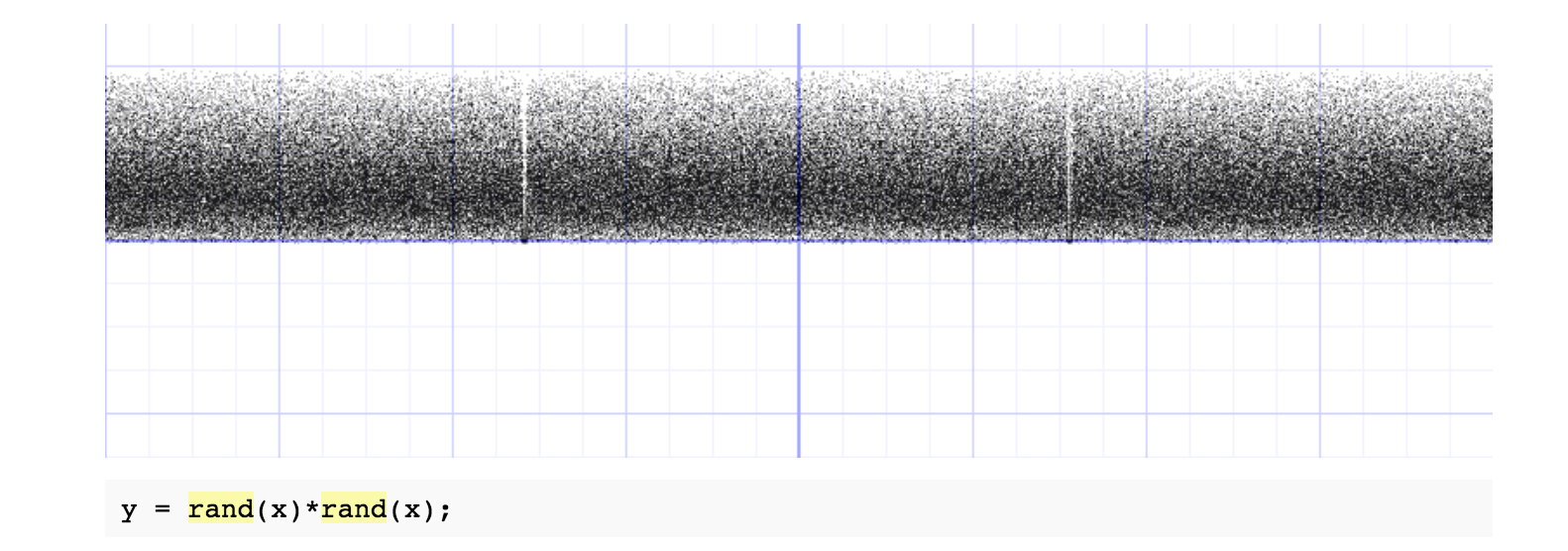
更多的随机研究可以看这篇文章,你会发现随机数也是可以「操作」的:
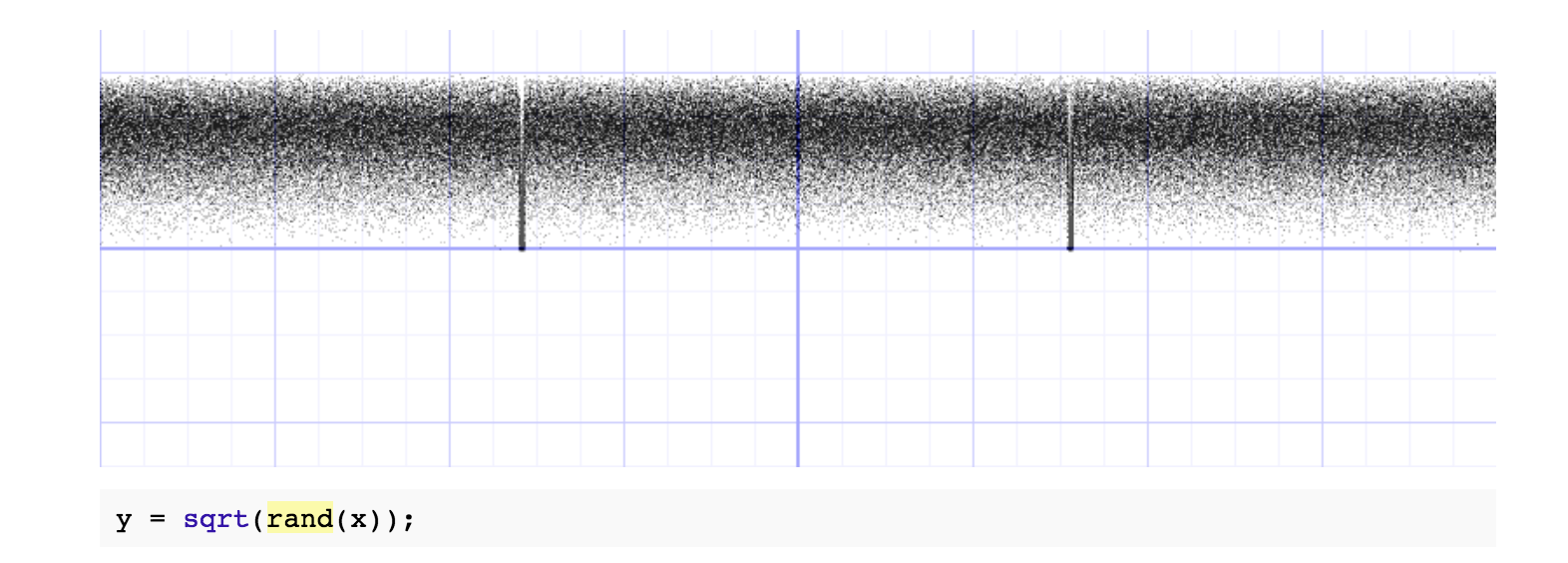
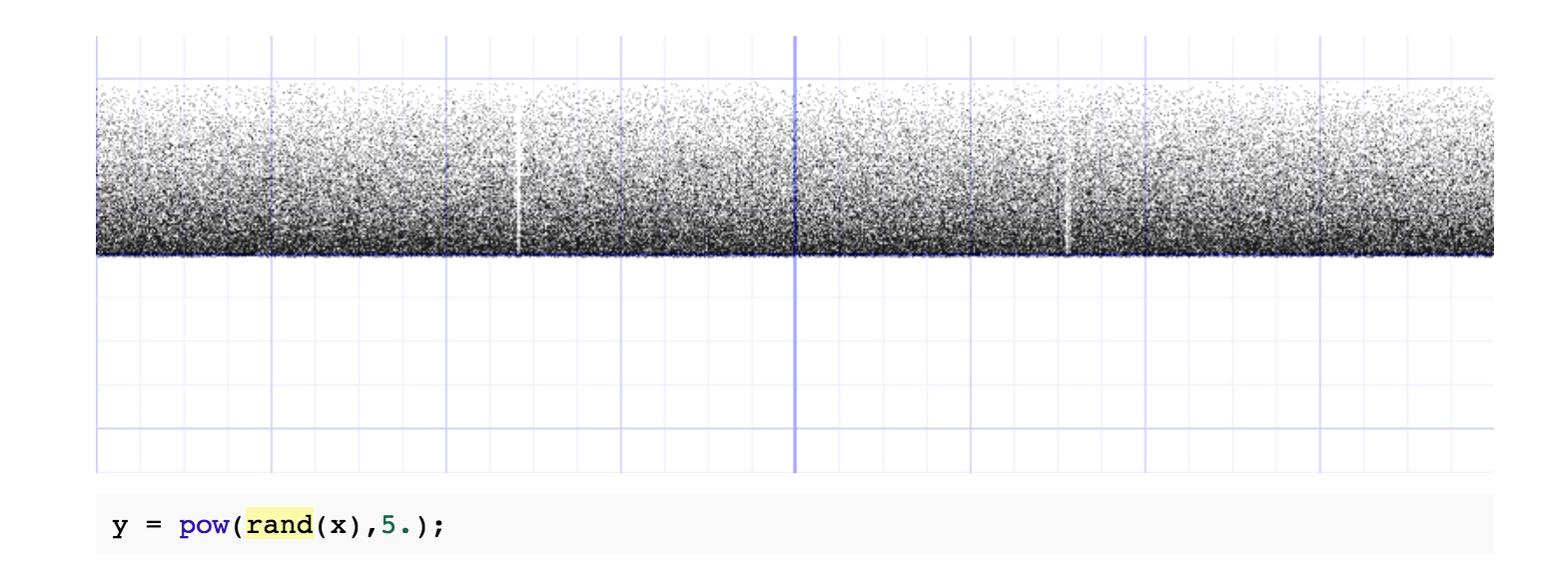
你会发现随机图表中,会有两个地方的随机分布不均匀(-1.5707 ~ 1.5707),这是 sin() 最大值和最小值的地方,所以我们在取值的时候尽量避免这两个地方:
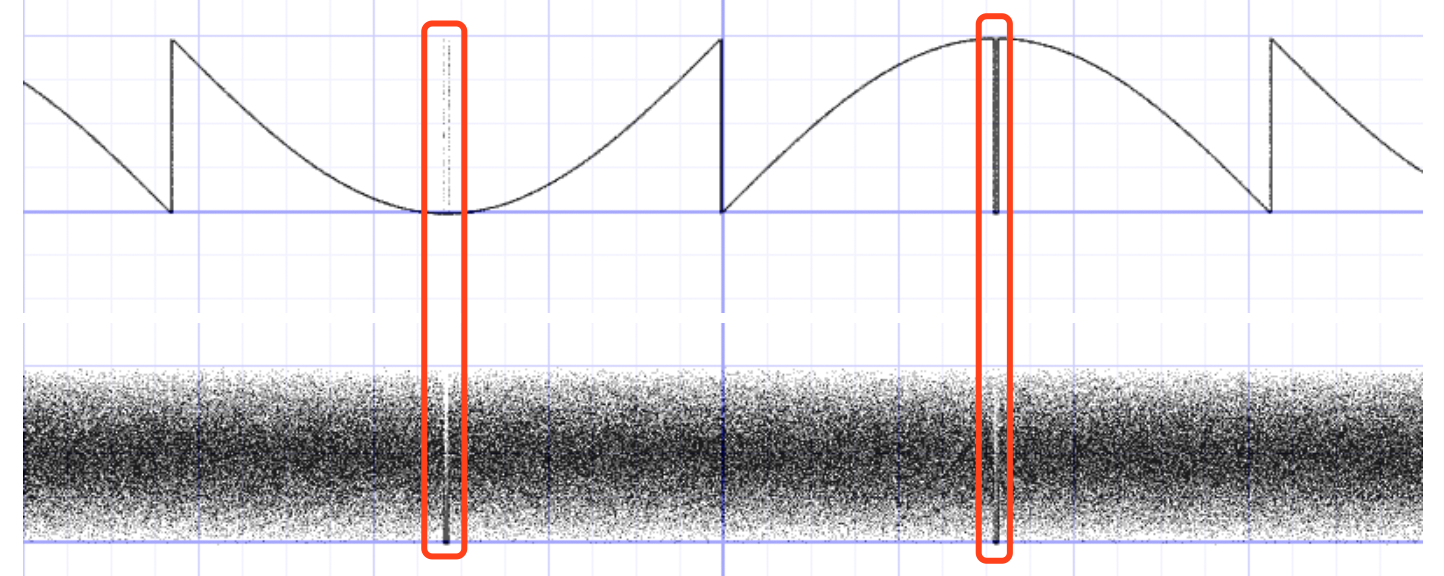
2D 随机
现在我们对随机有了深入的理解,是时候将它应用到二维,x 轴和 y 轴。为此我们需要将一个二维向量转化为一维浮点数。这里有几种不同的方法来实现,但 dot() 函数在这个例子中尤其有用。它根据两个向量的方向返回一个 0.0 到 1.0 之间的值。—— refer
如果你对下面的vec2(12.23,78.32)))*232348.23)留有疑问,姑且将其理解为 magic number,它的效果就跟电视没有信号时的雪花效果一样:
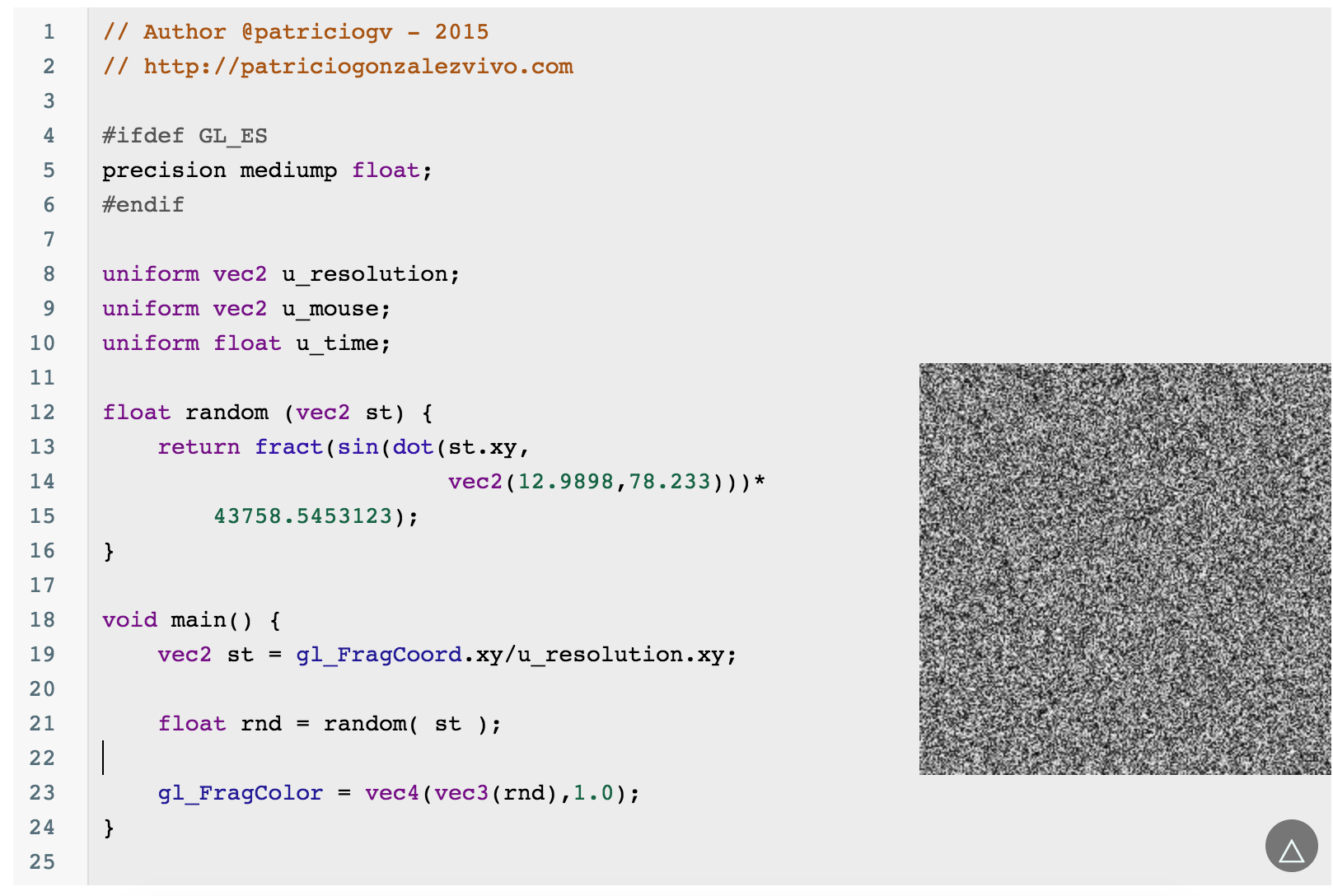
下面对这些随机数做一些操作:
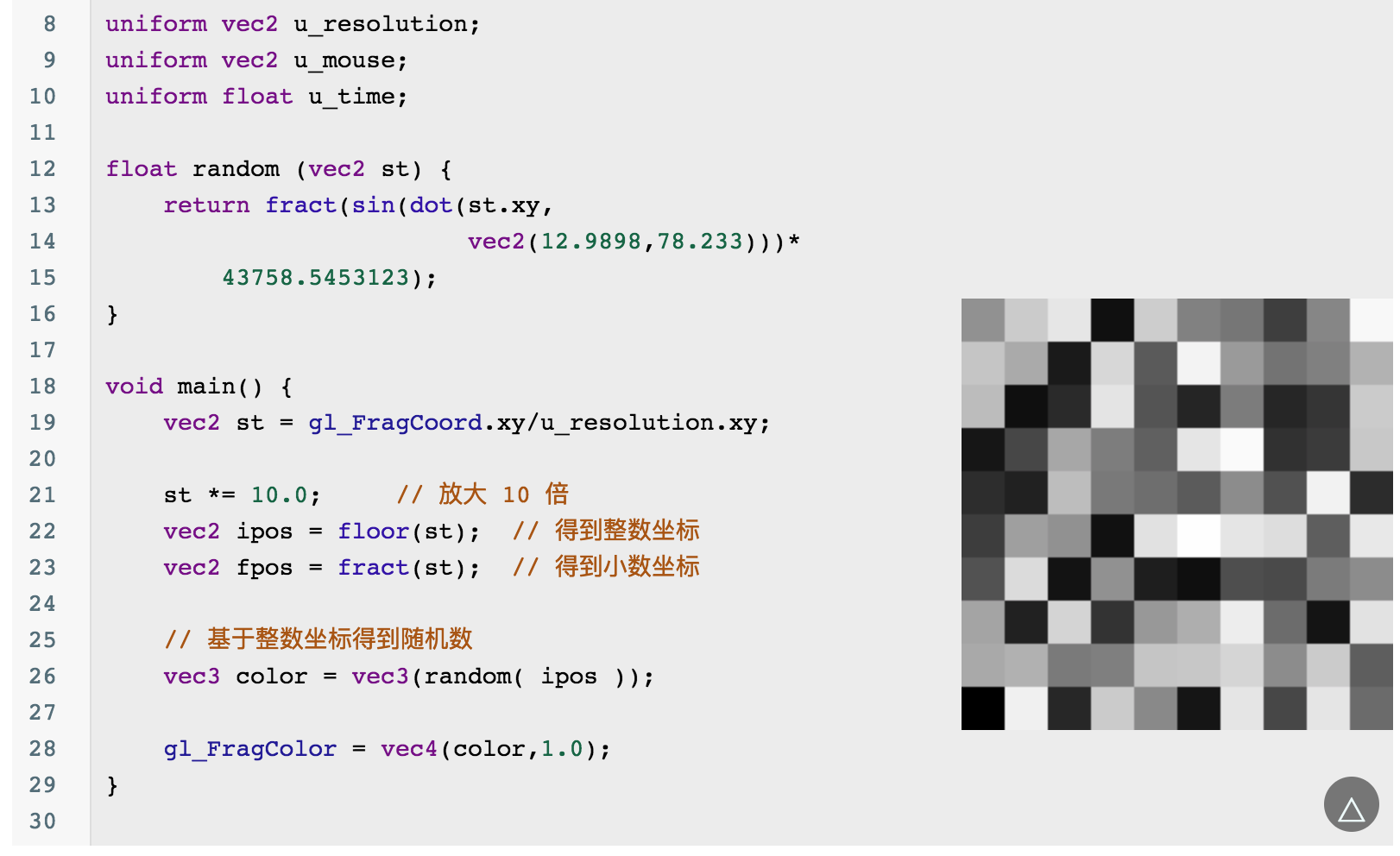
封装函数:
// 伪随机
float random (float n) {
return fract(sin(n)*1000000.);
}
float random (vec2 st) {
return fract(sin(dot(st.xy,vec2(12.9898,78.233)))*43758.5453123);
}
// 散列函数(哈希值)
float hash(float n) {
return fract(sin(n) * 1e4);
}
float hash(vec2 p) {
return fract(1e4 * sin(17.0 * p.x + p.y * 0.1) * (0.1 + abs(sin(p.y * 13.0 + p.x))));
}
二、噪声(noise)
噪声跟随机有什么不同?
噪音的基础来自于随机数,随机数的特点是每个点的值都是离散的,相互完全没有关系,而噪音则是让离散的随机数连续起来。最简单的连续化处理就是插值,在离散数据中间用函数插值的方法把空隙填满空间就自然连续了。说到插值,学过数值分析的立刻就能想到七八种插值方法,只要能保持连续性不管是三角函数,正态分布,还是样条曲线都可以使用。—— 不只是噪音
有了噪音我们就可以还原出自然界的真实景象:

如何得到一个离散的随机值,可以通过上面的随机函数:
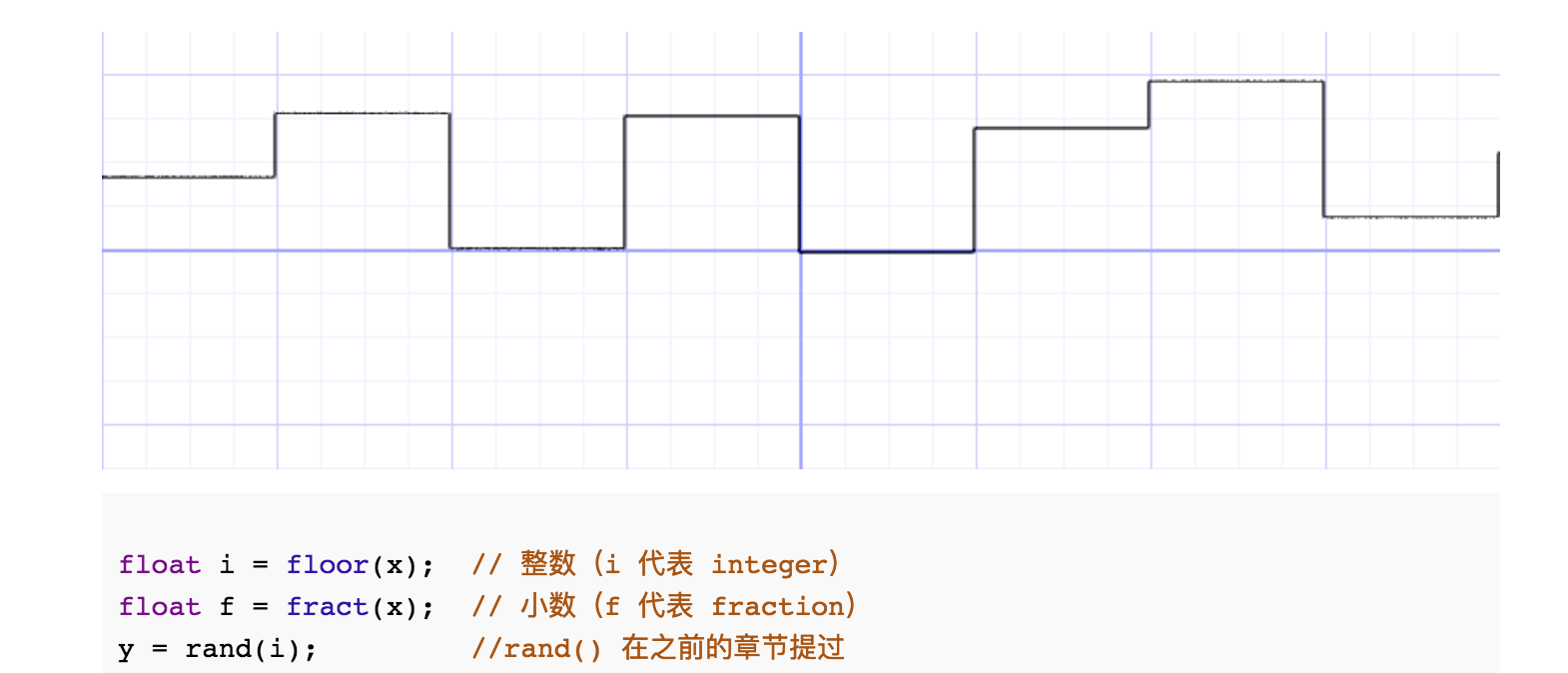
接着把这些离散的随机值通过mix()线性插值的方式连接起来:
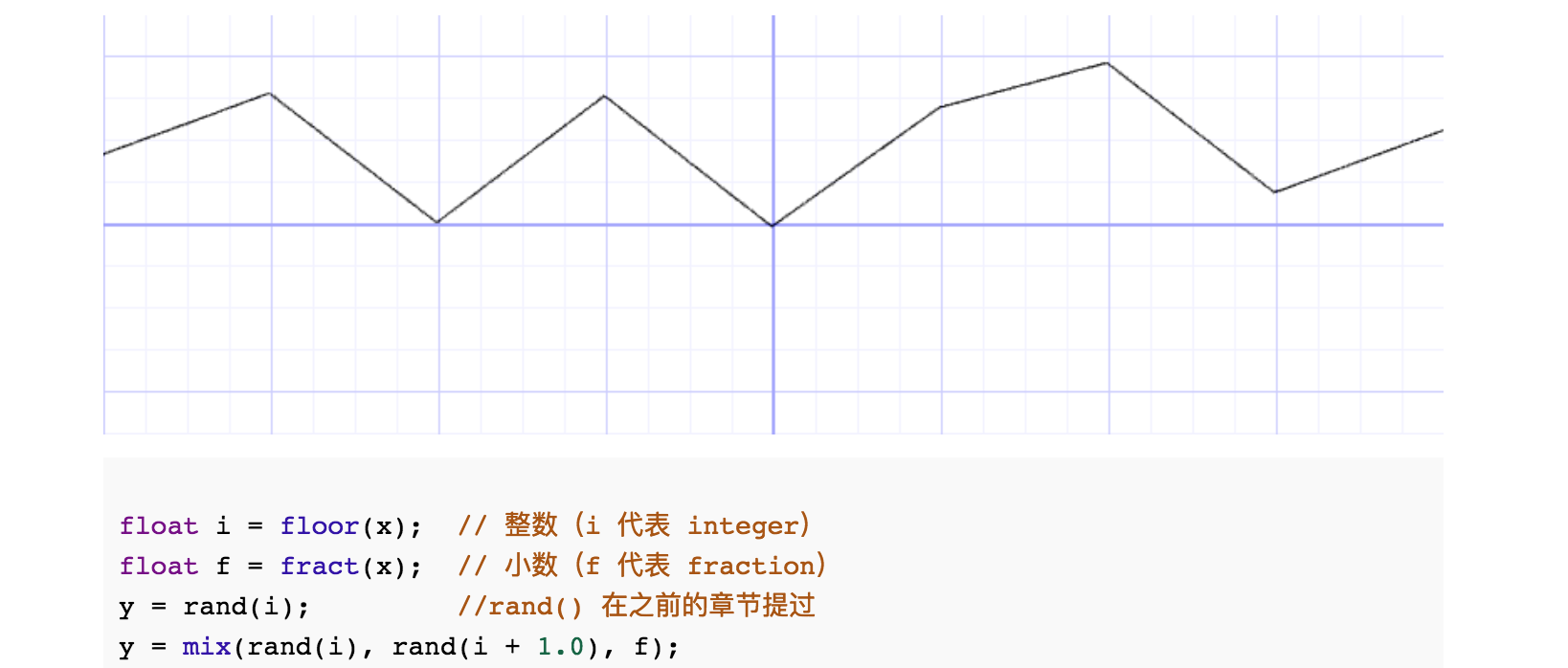
通过smoothstep()函数让变化更圆滑:
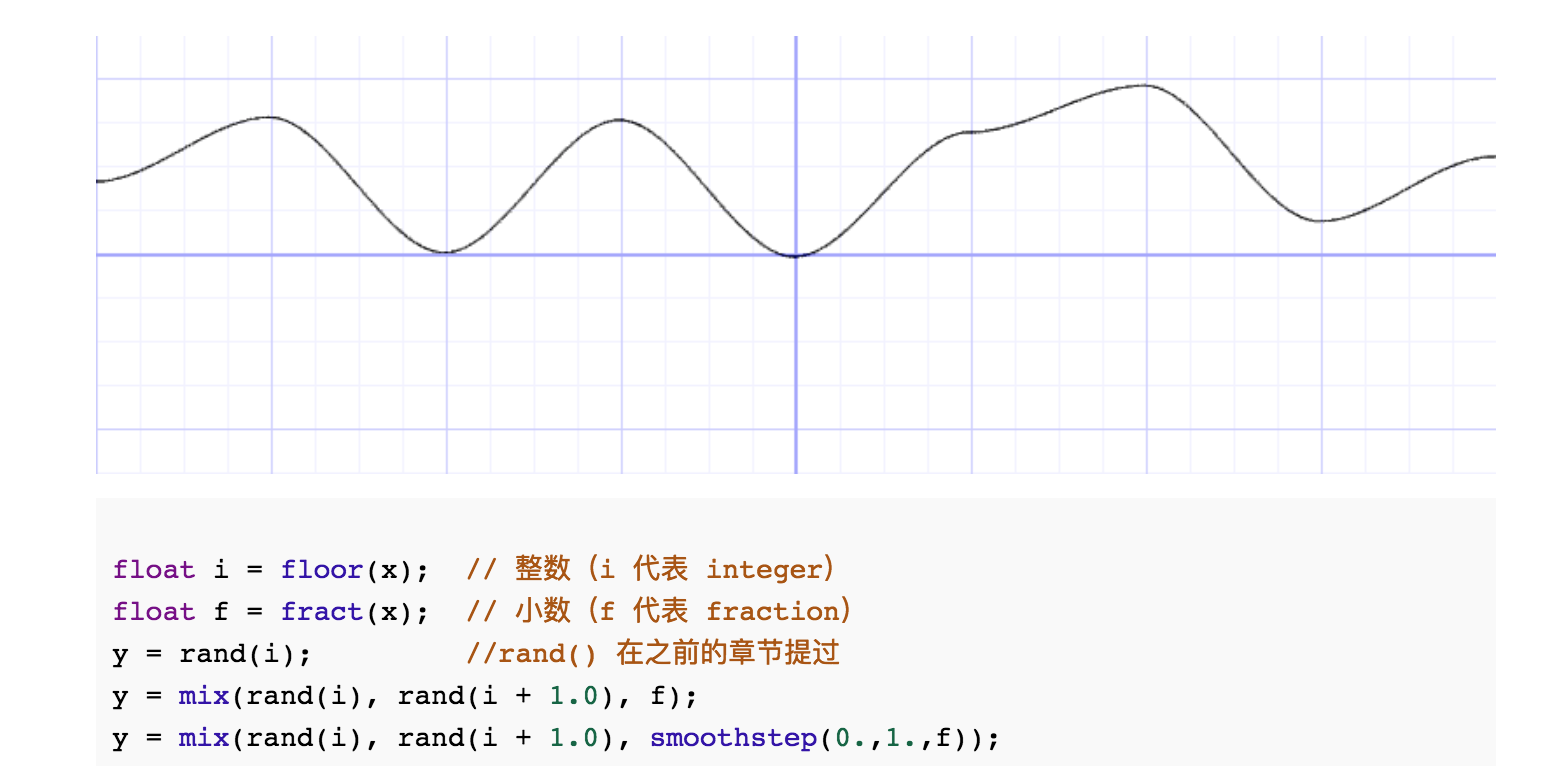
在一些 noise 的应用中你会发现程序员喜欢用他们自己的三次多项式函数(比如下面的例子),而不是用smoothstep(),结果是一样的。
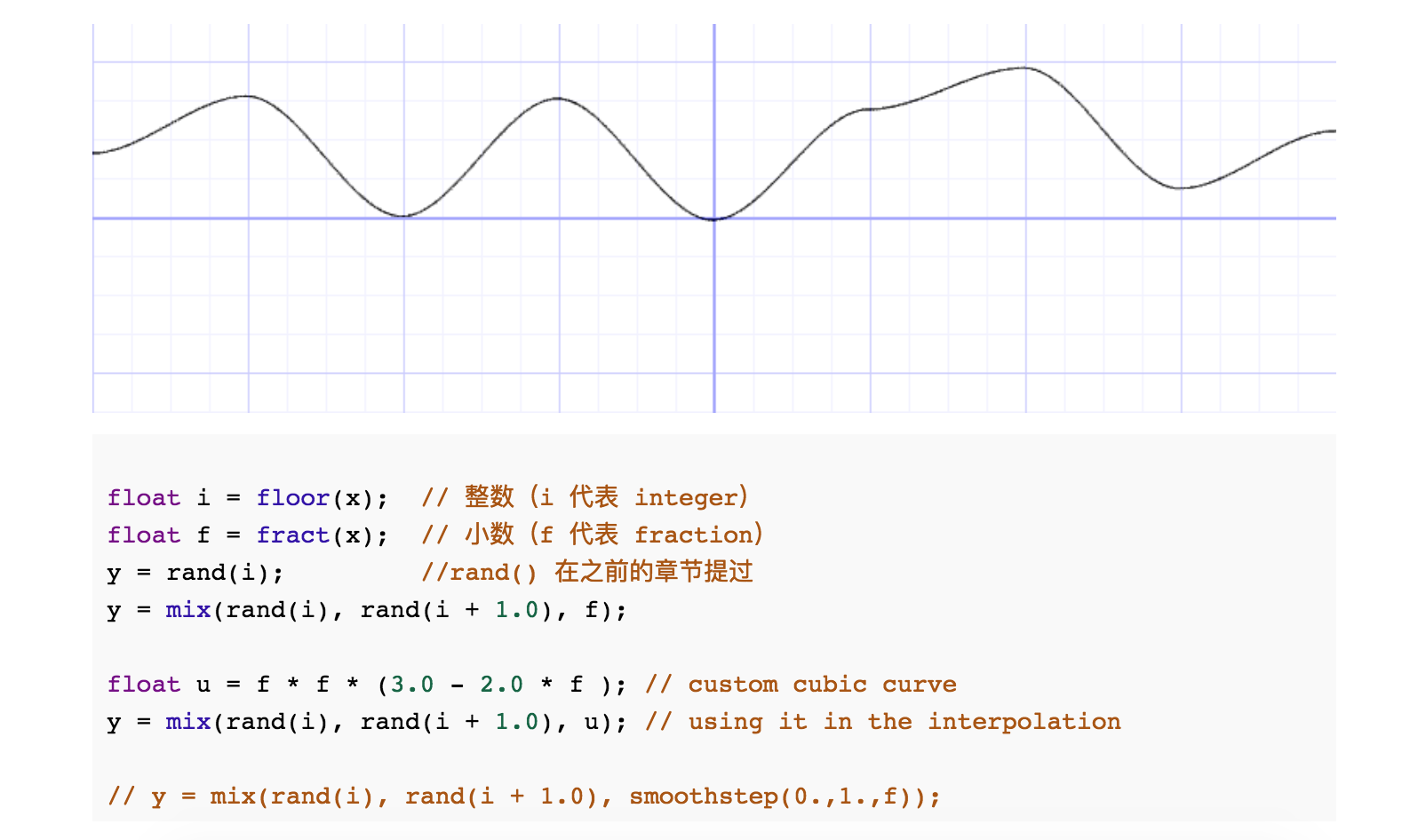
通过这种方式得到了一段 「噪音」。
当我们把它作为值,显示在画布中,会是什么样子呢?可以看到一维的噪音并没有太大的价值:

可以用直接封装好的noise()函数(文章底部会罗列这些函数的声明):

2D 噪声
2D 噪声在图形角度才更具备价值,其自变量不再是水平或垂直的一个值而是二维的值:
当我们使用已经封装好后的 2D noise() 函数并传入坐标后,看看效果:

函数封装:
// 一维(这里都是基于hash,也可以改成基于random
float noise(float x) {
float i = floor(x);
float f = fract(x);
float u = f * f * (3.0 - 2.0 * f);
return mix(hash(i), hash(i + 1.0), u);
}
// 二维
float noise(vec2 x) {
vec2 i = floor(x);
vec2 f = fract(x);
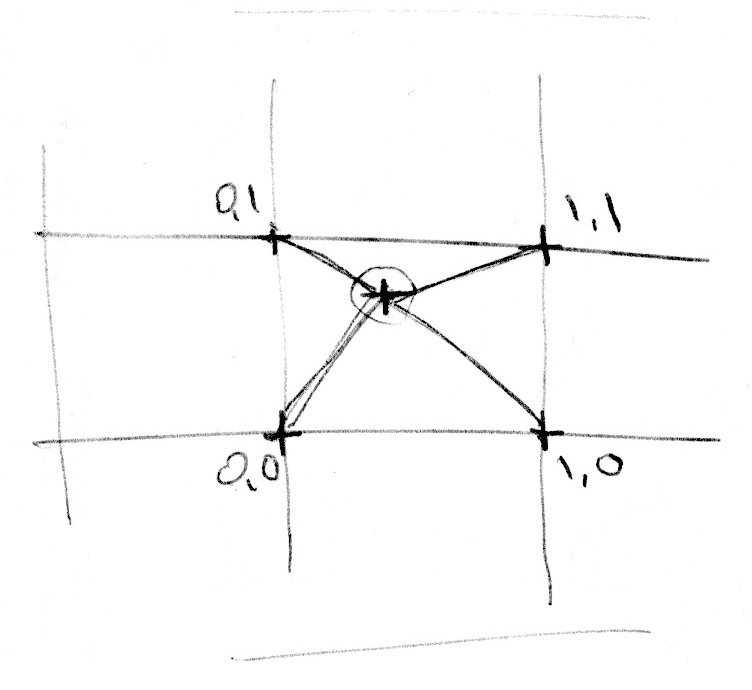
// Four corners in 2D of a tile
float a = hash(i);
float b = hash(i + vec2(1.0, 0.0));
float c = hash(i + vec2(0.0, 1.0));
float d = hash(i + vec2(1.0, 1.0));
// Simple 2D lerp using smoothstep envelope between the values.
// return vec3(mix(mix(a, b, smoothstep(0.0, 1.0, f.x)),
// mix(c, d, smoothstep(0.0, 1.0, f.x)),
// smoothstep(0.0, 1.0, f.y)));
// Same code, with the clamps in smoothstep and common subexpressions
// optimized away.
vec2 u = f * f * (3.0 - 2.0 * f);
return mix(a, b, u.x) + (c - a) * u.y * (1.0 - u.x) + (d - b) * u.x * u.y;
}
// 三维
float noise(vec3 x) {
const vec3 step = vec3(110, 241, 171);
vec3 i = floor(x);
vec3 f = fract(x);
// For performance, compute the base input to a 1D hash from the integer part of the argument and the
// incremental change to the 1D based on the 3D -> 1D wrapping
float n = dot(i, step);
vec3 u = f * f * (3.0 - 2.0 * f);
return mix(mix(mix( hash(n + dot(step, vec3(0, 0, 0))), hash(n + dot(step, vec3(1, 0, 0))), u.x),
mix( hash(n + dot(step, vec3(0, 1, 0))), hash(n + dot(step, vec3(1, 1, 0))), u.x), u.y),
mix(mix( hash(n + dot(step, vec3(0, 0, 1))), hash(n + dot(step, vec3(1, 0, 1))), u.x),
mix( hash(n + dot(step, vec3(0, 1, 1))), hash(n + dot(step, vec3(1, 1, 1))), u.x), u.y), u.z);
}
相关链接: