Logistic Regression笔记

2018-10-17 1,170 阅读7分钟

声明：本文由罗周杨原创，转载请注明作者和出处

本文是阅读斯坦福经典教材 Speech and Language Processing-Logistic Regression 所做的笔记，推荐看原文。

Logistic Regression可以用于二分类问题和多分类问题(Multinomial logistic regression)。逻辑回归是一种分类算法，并不是回归算法。逻辑回归属于判别式分类器（discriminative classifier），而朴素贝叶斯属于生成式分类器（generative classifier）。

判别式分类器和生成式分类器

为了区别这两种分类器，我们可以举一个简单的例子：区分照片里面的动物是猫还是狗。

Generative model的目标是，理解什么是猫什么事狗，然后做出判断。而Discriminative model则是紧紧学习怎样去区分这两种动物，而不是去学习它们是什么。

在数学上更直观的比较，首先看我们的niave Bayes分类公式：

\hat{c}=\mathop{\arg\max}_{c\in C}\overbrace{P(d\vert c)}^{\text{likelihood}} \overbrace{P(c)}^{\text{prior}}

对于generative model（例如naive Bayes）使用一个**似然(likelihood)**项来计算 $P(c\vert d)$ ，这个项表示的是如何生成一个文档的特征，如果我们知道它是类别c的话。而对于discriminative model，它会尝试直接去计算 $P(c\vert d)$ 。

基于概率的机器学习分类器的组成

基于概率的机器学习分类器有以下几个组成部分：

特征表示，即对每一个输入的表示
一个分类函数，用来估算当前输入的类别，例如sigmoid和softmax
一个目标函数，通常涉及在训练集上最小化误差，例如交叉熵损失函数
一个优化目标函数的算法，例如SGD

Sigmoid

二分类逻辑回归的目标是训练一个分类器，可以做出二分类决策，sigmoid就是可行的方式之一。

逻辑回归通过从训练集学习两个参数 $w$ 和 $b$ 来做出决策。

逻辑回归的类别估算公式如下：

z=(\sum_{i=1}^nw_ix_i)+b

要学习的两个参数在上式也有直接体现。

在线性代数里面，通常把上面的加权和 $\sum_{i=1}^nw_ix_i$ 用**点积(dot product)**来表示，所以上式等价于：

z=w\cdot x+b

那么得到的结果是一个浮点数，对于二分类为题，结果只有0和1两种，那我们怎么判断这个z是属于0类别还是1类别呢？

我们先看看sigmoid函数长什么样吧。

\sigma(z)=\frac{1}{1+e^{-z}}

图像如下：

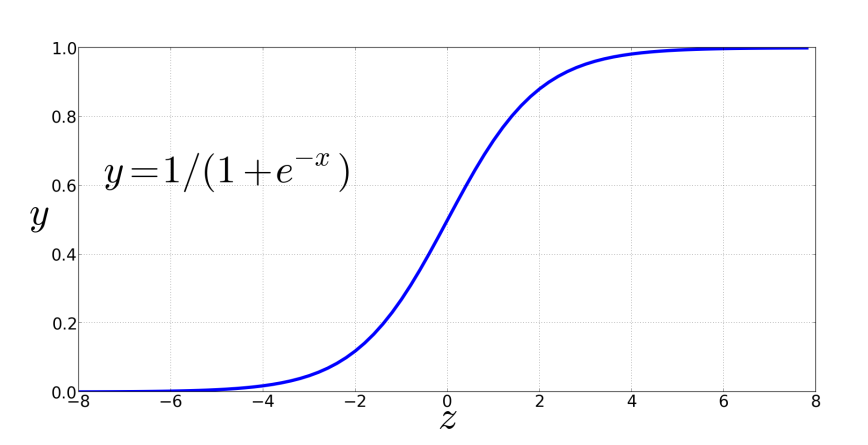
sigmoid funtion

可以看到，sigmoid函数的值域是(0,1)，并且是关于(0,0.5)对称的，所以很容易得到一个决策边界：

z<=0.5时属于0类别
z>0.5时属于1类别

sigmoid函数有很多很好的性质：

它的输入范围是 $(-\inf,\inf)$ ，输出值范围是 $(0,1)$ ，这就是天然的概率表示啊！
在x=0附近几乎是线性的，在非常负或者非常正的时候，变化不大

至此，我们可以计算类别0和类别1的概率：

P(y=1) = \sigma(w\cdot x +b) = \frac{1}{1+e^{-(w\cdot x+b)}}

P(y=0) = 1-P(y=1) = 1-\sigma(w\cdot x+b) = 1-\frac{1}{1+e^{-(w\cdot x+b)}} = \frac{e^{-(w\cdot x+b)}}{1+e^{-(w\cdot x+b)}}

cross-entropy损失函数

说到损失函数，你可能会想到均方差损失(MSE)：

L_{\text{MSE}}(\hat{y},y) = \frac{1}{2}(\hat{y}-y)^2

这个损失在线性回归里面用的很多，但是将它应用于概率分类的话，就变得难以优化了（主要是非凸性）。

条件似然估计(conditional maximum likelihood estimation)：选择参数 $w$ 和 $b$ 来最大化标签和训练数据之间（ $P(y\vert x)$ ）的对数概率。

因为类别的分布是一个伯努利分布(Bernoulli distribution)，所以我们可以很容易写出：

p(y\vert x) = \hat{y}^y(1-\hat{y})^{1-y}

因为，当y=1时， $p(y\vert x)=\hat{y}$ ，当y=0时， $p(y\vert x)=1-\hat{y}$ 。

由此，可以得到对数概率：

\log p(y\vert x) = \log[\hat{y}^y(1-\hat{y})^{1-y}] = y\log\hat{y}+(1-y)\log(1-\hat{y})

我们的训练过程就是要最大化这个对数概率。如果对上式两边取负数，最大化问题就变成了最小化问题，即训练的目标就是最小化：

L_{CE}(\hat{y},y)=-\log p(y\vert x)=-[y\log\hat{y}+(1-y)\log(1-\hat{y})]

又因为 $\hat{y}=w\cdot x+b$ ，所以我们的负对数似然损失公式为：

L_{CE}=-[y\log\sigma(w\cdot x+b)+(1-y)\log(1-\sigma(w\cdot x+b))]

这也就是我们的交叉熵损失(cross-entorpy loss)，至于为什么是这个名称，因为上述公式就是： $y$ 的概率分布和估计分布 $\hat{y}$ 之间的交叉熵。

所以，在整个批量的数据上，我们可以得到平均损失为：

Cost(w,b) = \frac{1}{m}\sum_{i=1}^mL_{CE}(\hat{y}^{(i)},y^{(i)}) = -\frac{1}{m}\sum_{i=1}^m y^{(i)}\log\sigma(w\cdot x^{(i)}) + (1-\hat{y}^{(i)})\log(1-\sigma(w\cdot x^{(i)}+b))

梯度下降

梯度下降的目标就是最小化损失，用公式表示就是：

\hat{\theta} = \mathop{\arg\min}_{\theta}\frac{1}{m}\sum_{i=1}^mL_{CE}(y^{(i)},x^{(i)};\theta)

对于我们的Logistic Regression， $\theta$ 就是 $w$ 和 $b$ 。

那么我们如何最小化这个损失呢？梯度下降就是一种寻找最小值的方式，它是通过倒数来得到函数的最快衰减方向来完成的。

对于逻辑回归的这个损失函数来说，它是凸函数(convex function)，所以它只有一个最小值，没有局部最小值，所以优化过程中肯定可以找到全局最小点。

举个二维的例子，感受一下这个过程，如下图所示：

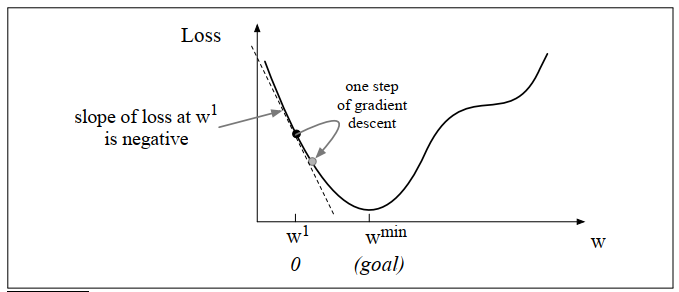
gredient decent example

可见，上述损失函数的优化过程就是每次向着梯度的正方向移动一小步!可以用公式表示如下：

w^{t+1} = w^t - \eta\frac{\partial}{\partial w}f(x;w)

上面 $\eta$ 决定了这个一小步是多少，也称作学习率(learning rate)。

上面的梯度 $\frac{\partial}{\partial w}f(x;w)$ 结果是一个常数。

如果是N维空间呢？那么梯度就是一个矢量了，如下所示：

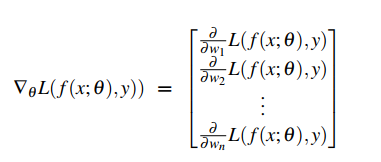
那么，我们的参数更新就是：

\theta_{t+1}=\theta_t - \eta\nabla L(f(x;\theta),y)

Logistic Regression的梯度

逻辑回归的损失如下：

L_{CE}(w;b)=-[y\log\sigma(w\cdot x+b)+(1-y)\log(1-\sigma(w\cdot x+b))]

我们有：

\frac{\partial L_{CE}(w,b)}{\partial w_j} = [\sigma(w\cdot x+b)-y]x_j

对于一个批量的数据，我们的梯度如下：

\frac{\partial Cost(w,b)}{\partial w_j} = \sum_{i=1}^m[\sigma(w\cdot x^{(i)}+b)-y^{(i)}]x_j^{(i)}

正则化

上面训练的模型可能会出现过拟合(overfitting)，为了解决这个问题，我们需要一项技术，叫做正则化(regularization)。

正则化是对权重的一种约束，更细致一点地说，是在以最大化对数概率 $\log P(y\vert x)$ 的前提下，对权重 $w$ 的约束。

所以我们的目标可以用下面的公式描述：

\hat{w} = \mathop{\arg\max}_w\sum_{i=1}^m\log P(y^{(i)}\vert x^{(i)})-\alpha R(w)

其中， $R(w)$ 就是正则项(regularization term)。

上式可以看出，正则项是为了惩罚大的权重。我们总是倾向于，在效果差不多的模型中，选择 $w$ 更少的那一个。所谓 $w$ 更少就是 $w$ 的特征更少，即指 $w$ 的向量中0的个数更多的。

常用的正则化方式有L2正则和L1正则。

L2正则计算的是欧氏距离，公式如下：

R(W) = ||W||^2 = \sum_{j=1}^Nw_j^2

L1正则计算的是马哈顿距离，公式如下：

R(W) = ||W||_1 = \sum_{i=1}^N|w_i|

那么L2正则和L1正则有什么优缺点呢？

L2正则比较容易优化，因为它的导数就是 $2w$ ，而L1的导数在0出不连续
L2正则更偏向于需要小的权重值，L1正则更偏向于某些权重值更大，但是同时也更多的权重值为0，也就是说L1正则化的结果倾向于稀疏的权重矩阵。

L1和L2正则都有贝叶斯解释。L1正则可以解释为权重的Laplace先验概率，L2正则对应这样一个假设：权重的分布是一个均值为0( $\mu = 0$ )的正态分布。

权重的高斯分布如下：

\frac{1}{\sqrt{2\pi\sigma_j^2}}\exp(-\frac{(w_j-\mu_j)^2}{2\mu_j^2})

根据Bayes法则，我们的权重可以用以下公式估算：

\hat{w} = \mathop{\arg\max}_w\prod_{i=1}^M P(y^{(i)}\vert x^{(i)})\times P(w)

使用上面的高斯分布计算先验概率 $P(w)$ ，可以得到：

\hat{w} = \mathop{\arg\max}_w\prod_{i=1}^M P(y^{(i)}\vert x^{(i)})\times \prod_{j=1}^n\frac{1}{\sqrt{2\pi\sigma_j^2}}\exp(-\frac{(w_j-\mu_j)^2}{2\mu_j^2})

我们让 $\mu = 0$ ， $2\sigma^2 = 1$ ，取对数，则有：

\hat{w} = \mathop{\arg\max}\sum_{i=1}^m\log P(y^{(i)}\vert x^{(i)})-\alpha\sum_{j=1}^nw_j^2

Multinomial logistic regression

上面我们讨论的都是二分类问题，如果我们想要多分类呢？这个时候就需要Multinomial logistic regression了，这种多分类也叫作softmax regression或者maxent classifier。

多分类的类别集合就是不 $[0,1]$ 两种了，所以我们更换一个给输出结果计算概率的函数，用来替代sigmoid,那就是sigmoid的泛华版本softmax。

\text{softmax}(z_j) = \frac{e^{z_i}}{\sum_{j=1}^ke^{z_j}}

其中， $1\leq i \leq k$ 。

所以，对于输入

z = [z_1,z_2,\dots,z_k]

我们有：

\text{softmax} = [\frac{e^{z_1}}{\sum_{i=1}^ke^{z_i}},\frac{e^{z_2}}{\sum_{i=1}^ke^{z_i}},\dots,\frac{e^{z_k}}{\sum_{i=1}^ke^{z_i}}]

显然，softmax函数的分母是一个累加，因此softmax对于每一个输入，都输出一个概率值，并且所有输入的概率值和为1！

和sigmoid类似，把 $z=w\cdot x+b$ 带入：

p(y=c\vert x) = \frac{e^{w_c\cdot x+b_c}}{\sum_{j=1}^k e^{w_j\cdot x+b_j}}

注意的是，我们的 $w$ 和 $b$ 都是对应此时的分类的，所以写成 $w_c$ 和 $b_c$ 。

同样的，我们的损失函数也变成了泛化版本：

L_{CE}(\hat{y},y) = -\sum_{k=1}^K 1\{y=k\}\log p(y=k\vert x) = -\sum_{k=1}^K 1\{y=k\}\log\frac{e^{w_k\cdot x+b_k}}{\sum_{j=1}^Ke^{w_j\cdot x+b_j}}

其中，1{y=k}表示 $y=k$ 时值为1，否则为0。

因此，可以得到下面的导数(没有推导过程)：

\frac{\partial L_{CE}}{\partial w_k} = (1\{y=k\} - p(y=k\vert x))x_k = (1\{y=k\}-\frac{e^{w_k\cdot x+b_k}}{\sum_{j=1}^Ke^{w_j\cdot x+b_j}})x_k

思考题

logistic regression和神经网络是不是很相似呢？你能说出它们的异同吗？

联系我

WeChat: luozhouyang0528
Email: stupidme.me.lzy@gmail.com
公众号: stupidmedotme

友情链接：