Lintcode第二题

这是Lintcode第二题，原题在此 尾部的零。题目虽然标为“简单”，但答对率却不高。

看到这一题，比较直观的想法是计算从1到n的连乘，但这样很容易溢出，因为乘起来的数字太大。

换一个思路，我们将n阶乘做质因数分解，将n阶乘表示成

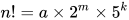
其中a, m, n都是非负整数，且a不能被2和5整除。

上面的表达式中，每一对2和5都贡献了一个末尾的零，所以我们只要知道n的阶乘中有多少个因子2，有多少个因子5，求两者的最小值

就是末尾零的个数了。

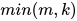
我们先来看一下n的阶乘有多少个因子5。

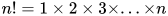
从1到n中，每一个5的倍数都至少贡献了一个5，比如数字5，10，15，都贡献了一个5。每个

的倍数都至少贡献了两个5，比如数字25，50。所以n的阶乘中包含的5的因子的个数，可以用下面的表达式来计算

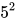
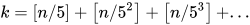
同样的，n的阶乘包含的2的因子的个数可以用下面的表达式计算

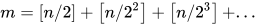
很显然 m > k。前面说过，末尾零的个数是

也就是k了。

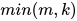
理解了上面的步骤，接下来就可以用代码来实现算法了，如下

def trailing_zero_num(n):
    num = 0

    while True:
        n = int(n / 5)
        if n == 0:
            break
        num = num + n

    return num