[译] 降维技术中常用的几种降维方法

leeyangtju
2,090 阅读18分钟

在本文中，我将尽最大的努力来阐明降维技术中常用的三种降维方法：即 PCA、t-SNE 和自动编码器。本文的动机是由于这些方法多被当作黑盒使用，而有时会被误用。理解它们将可以帮助大家决定何时以及如何使用它们。

我将使用 TensorFlow 从头开始介绍每个方法的内部结构和对应代码（其中不包括 t-SNE）。为什么使用 TensorFlow？因为它主要用于深度学习，让我们使用它做一些其它的挑战性任务 :) 本文的代码可以在这个笔记中找到。

动机

在处理实际问题和实际数据时，我们通常面临的是高达百万维度的数据。

虽然数据在其原始高维结构中更能够表达自己的特性，但有时候我们可能需要降低它的维度。 一般需要减少维度的通常与可视化相关（减少到 2 到 3 个维度上，这样我们就可以绘制它），但情况并非总是如此。

有时，在实际应用中我们可能认为性能比精度更重要，这样我们就可以把 1000 维的数据降低到 10 维，这样我们就能更快地处理它（比如在距离计算中）。

有时纬度降低的需求是真实存在的，并且有很多的应用。

在开始之前，如果你必须为下列情况选择一种降维技术，那么你会选择哪一种呢？

  1. 你的系统使用余弦相似度来度量距离，但是你需要把它进行可视化，展示给一些没有技术背景的董事会成员，他们可能根本不熟悉余弦相似度的概念 —— 你会怎么做呢？

  2. 你需要将数据压缩到尽可能小的维度，并且你得到的约束条件是保持大约 80% 的数据，你又会怎么做呢？

  3. 你有一个数据库，其中包含经过长时间收集的某类数据，并且数据（类似的类型）不断地添加进来。

你需要降低数据的维度，无论是目前已有的数据还是源源不断的新数据，你会选择哪种方法呢？

我希望本文能帮助你更好地理解降维，这样你就能处理好类似的问题。

让我们从 PCA 方法开始。

PCA 方法

PCA（Principal Component Analysis）方法大概是书本中最古老的降维技术了。

因此 PCA 已经得到了很好的研究，并且很多的方法也可以得到相同的解，我们将在这里讨论其中的两种方法，即特征分解和奇异值分解（SVD），然后我们将在 TensorFlow 中实现 SVD 方法。

从现在开始，X 为我们要处理的数据矩阵，形状为 (n, p)，其中 n 表示样本数量，p 表示维度。

给定 X，以上这两种方法都试图以它们自己的方式，来处理和分解 X，之后我们可以将分解后的结果相乘，以在更小的维数中表示最多的信息。我知道这听起来很可怕，所以这里我将省去大部分的数学知识，只保留有助于理解这些方法优缺点的部分。

因此特征分解和奇异之分解是两种不同的矩阵分解方法，让我们看看它们在主成分分析中有什么用，以及它们之间有什么联系。

先看一眼下面的流程图，我马上就会解释其中的内容。

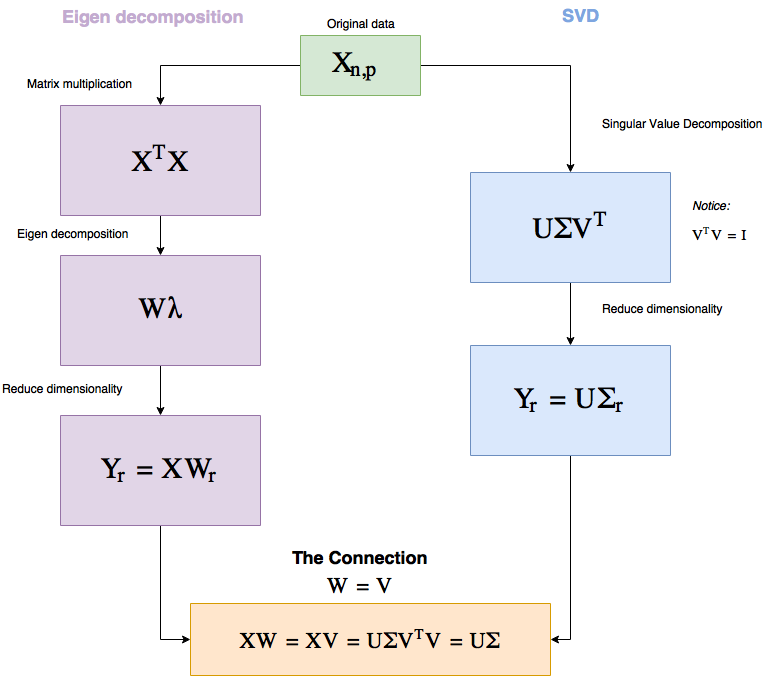
图 1 PCA 工作流图

为什么要关心这个呢？因为这两个过程中有一些非常基本的东西，它们可以告诉我们很多关于主成分分析（PCA）的知识。

正如你所看到的这样，这两种方法都是纯粹的线性代数方法，这基本上告诉我们，使用 PCA 方法就是从不同的角度观察真实数据 —— 这是 PCA 方法独有的，而其它的方法则是将数据从低维进行随机表示，并且试图让它表现得像高维度数据一样。

另外值得注意的是，所有的操作都是线性的，所以使用 SVD 的方法速度非常快。

同样给定相同的数据，PCA 方法总是能给出相同的答案（另外两种方法则不是这样）。

注意到在 SVD 方法中我们如何选择参数 r（r 是我们想要降到的维度）对于更低的维度来说能够保留更大的 Σ 值？ 其中 Σ 有一些特别之处。

Σ 是一个对角矩阵，其中有 p（p 为维度大小）个对角值（一般又称为奇异值），并且它们的大小表示了它们对于信息保存的重要性。

因此我们可以选择将维度减少，且减少到一个要大约保留的维度数量。给定一个维度数量的百分比，然后我将在代码中演示它（比如在丢失最多 15% 的数据约束下，我们给出的减少维度的能力）。

正如你看到的一样，使用 TensorFlow 实现这个功能是相当简单的 —— 我们只需要编写一个类，该类中包含有一个 fit 方法和 reduce 方法即可，我们需要提供的参数是需要降维到的维度。

代码（PCA）

让我们来看一下 fit 方法是什么样的，这里的 self.X 包含参与计算的数据，并且其类型为 self.dtype=tf.float32。

def fit(self):
    self.graph = tf.Graph()
    with self.graph.as_default():
        self.X = tf.placeholder(self.dtype, shape=self.data.shape)

        # 执行 SVD 方法
        singular_values, u, _ = tf.svd(self.X)

        # 创建 sigma 矩阵
        sigma = tf.diag(singular_values)

    with tf.Session(graph=self.graph) as session:
        self.u, self.singular_values, self.sigma = session.run([u, singular_values, sigma],
                                                               feed_dict={self.X: self.data})

因此方法 fit 的目的是创建我们后面会使用到的 Σ 和 U。 我们从 tf.svd 这一行开始，它给我们计算出了对应的奇异值，也就是图 1 中表示为 Σ 的对角线的值，同时它也计算出了 U 和 V 矩阵。

然后 tf.diag 是 TensorFlow 中将一维向量转换成对角线矩阵的方法，这里将奇异值转换成对角线矩阵 Σ。

在 fit 方法的最后我们就可以计算出奇异值、矩阵 Σ 和 U。

现在让我们来实现 reduce 方法。

def reduce(self, n_dimensions=None, keep_info=None):
    if keep_info:
        # 奇异值规范化
        normalized_singular_values = self.singular_values / sum(self.singular_values)

        # 为每个维度创建保存信息的梯形累计和
        ladder = np.cumsum(normalized_singular_values)

        # 获取超过给定信息阈值的第一个索引
        index = next(idx for idx, value in enumerate(ladder) if value >= keep_info) + 1
        n_dimensions = index

    with self.graph.as_default():
        # 从 sigma 中删去相关部分
        sigma = tf.slice(self.sigma, [0, 0], [self.data.shape[1], n_dimensions])

        # PCA 方法
        pca = tf.matmul(self.u, sigma)

    with tf.Session(graph=self.graph) as session:
        return session.run(pca, feed_dict={self.X: self.data})

如上所示，reduce 方法接受参数 keep_info 或者 n_dimensions（这里我没有写输入检查，输入检查是必须要有的呀）。
如果使用时提供参数 n_dimensions，该方法会简单将数据维度降低到该值，但是如果我们使用时提供参数 keep_info，该参数是一个 0 到 1 的浮点数，那么该方法就需要保留原始数据的该数据对应百分比（比如 0.9 —— 表示保留原始数据的 90%）。 在第一个 “if” 判断语句中，我们将数据进行了归一化，并且检查了需要使用多少个奇异值，接下来基本上是从 keep_info 中求出 n_dimensions 的值。

在图中，我们只是把 Σ（sigma） 矩阵进行切片以对应尽可能多的需求数据，然后我们执行矩阵乘法。

让我们在鸢尾花（iris）数据集上试一下，这是包含有 3 种形状为（150,4）的鸢尾花数据集。

from sklearn import datasets
import matplotlib.pyplot as plt
import seaborn as sns

tf_pca = TF_PCA(iris_dataset.data, iris_dataset.target)
tf_pca.fit()
pca = tf_pca.reduce(keep_info=0.9)  # Results in 2 dimensions

color_mapping = {0: sns.xkcd_rgb['bright purple'], 1: sns.xkcd_rgb['lime'], 2: sns.xkcd_rgb['ochre']}
colors = list(map(lambda x: color_mapping[x], tf_pca.target))

plt.scatter(pca[:, 0], pca[:, 1], c=colors)

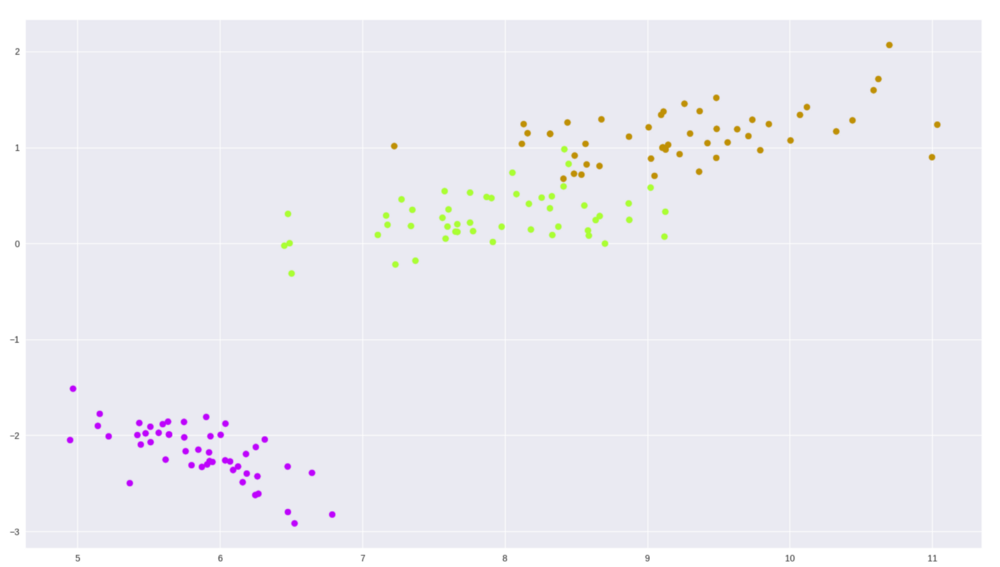
图 2 在 Iris 数据集上通过 PCA 方法进行二维展示

还不错，对吧？

t-SNE 方法

t-SNE 相对于 PCA 来说是一个相对较新的方法，源自于 2008 年的一篇论文（原始论文链接）。

它比 PCA 方法理解起来要复杂，所以请耐心听我说。
我们对 t-SNE 的表示法是这样的，X 表示原始数据，P 是一个矩阵，它保存着高维（原始）空间中 X 的点之间的亲密程度（即距离），Q 也是一个矩阵，它保存着低维空间中数据点之间的亲密程度。如果我们有 n 个数据样本，Q 和 P 都是 n×n 的矩阵（即从任意点到包括它自身在内的任意点之间的距离）。

现在 t-SNE 方法有它自己“独特的方式”（我们将很快介绍）来衡量物体之间的距离，一种测量高维空间中数据点之间的距离的方法，而另外一种方法是在低维度空间中测量数据点之间的距离，还有第三种方法是度量 P 和 Q 之间的距离的方法。 从原始文献可知，一个点 x_j 与另一个点 x_i 的相似度由 _p_j|i 给出，其中，如果在以 x_i 为中心的高斯分布下，按其概率密度的比例选取邻点 x_j。

“什么？”别担心，就像我说的那样，t-SNE 有它自己的距离测量方法，所以我们来看一下距离（亲密程度）测量公式，从中找出一些解释来理解 t-SNE 的行为。

从高级层面来说，这就是该算法的工作原理（注意，它与 PCA 不同，它是一种迭代算法）。

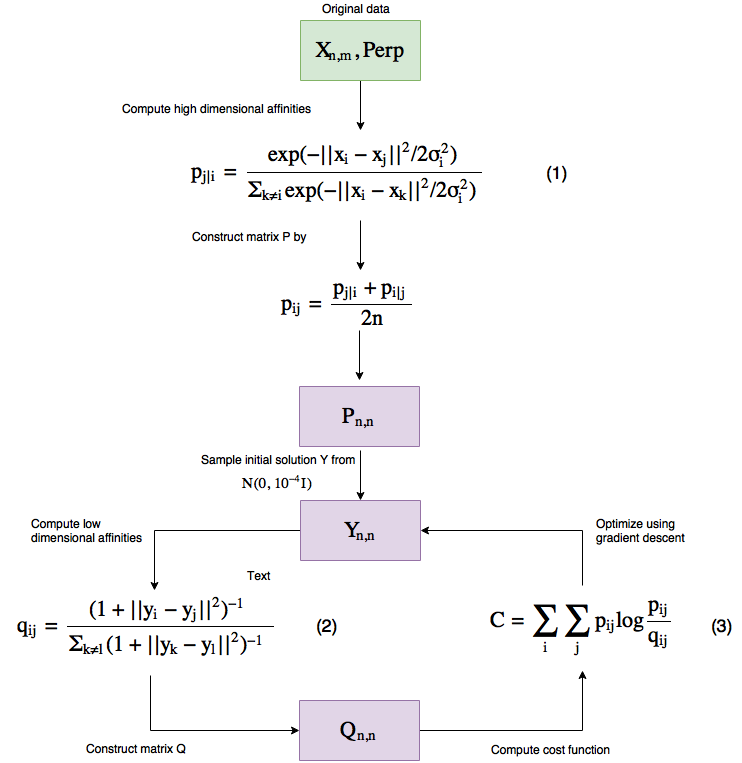
图 3 t-SNE 工作流

让我们一步一步来。

该算法接受两个输入，一个是数据本身，另一个是复杂度（Perp）。

复杂度简单来讲就是你想要如何平衡在优化过程中的数据局部（关闭点）结构和全局结构之间的焦点 —— 本文建议将其保持在 5 到 50 之间。

较高的复杂度意味着数据点会考虑更多的点作为其近邻点，较低的值则意味着考虑较少的点。

复杂度真的会影响到可视化效果，并且一定要小心，因为它会在低维数据的可视化中产生一些误导现象 —— 因此我强烈建议阅读这篇非常好的文章如何正确使用 t-SNE，这篇文章涉及到了复杂度取值不同的影响。

这种复杂度从何而来？它是用来计算出方程 （1）中的 σ_i，因为它们有一个由二叉搜索树构成的单调连接。

因此 σ_i 基本上是使用我们为算法提供的复杂度数据，以不同的方式计算出来的。

让我们来看一下 t-SNE 中的公式能够告诉我们什么。

在我们研究方程（1）和方程（2）之前需要知道的是，p_ii 被设置为 0，q_ii 也被设置为 0（这只是一个给定的值，我们将它应用于两个相似的点，方程不会输出 0）。

所以我们来看方程（1）和方程（2），请注意，如果两个点是接近的（在高纬度结构表示下），那么分子将产生一个约为 1 的值，而如果它们相距很远，那么我们会得到一个无限小的值 —— 这在后面将有助于我们理解成本函数。

现在我们已经看到了 t-SNE 的一些性质。

一个是由于关联关系方程的建立方式的原因，在 t-SNE 图中解释距离是有问题的。

这意味着集群之间的距离和集群大小可能会产生误导，并且也会受到所选择的复杂度大小的影响（再次提醒，我将参考上面文中提到的文章中的方法，以查看这些现象的可视化数据）。

另外一件需要注意的事情是方程（1）中我们如何计算点与点之间的欧氏距离的？这里非常强大的地方是，我们可以将距离度量切换成其它任何我们想要使用的距离度量方法，比如余弦距离、曼哈顿距离等等（只要保持空间度量即可），并保持低维结构下的亲和力是相同的 —— 这将以欧几里德距离方式下，导致绘制比较复杂的距离。

举个例子，如果你是 CTO，并且有一些数据，你想要使用余弦相似性来作为其距离度量，而你的 CEO 希望你现在来做一些展示来表现这些数据的特性，我不确定你有时间来向董事会解释余弦相似性以及如何操作集群数据，你只需要简单地绘制出余弦相似集群即可，这正如在 t-SNE 算法中使用的欧几里德距离集群一样 —— 这就是我想说的，这已经很好了。

在代码中，你可以在 scikit-learn 中通过提供一个距离矩阵来使用 TSNE 方法来实现这些。

好了，现在我们知道了，如果 x_i 和 x_j 相距很近时，p_ij/q_ij 的值就会很大，相反地，相距很远时其值就会很小。

让我们通过绘制出其图像来看一下我们的损失函数（我们称之为 Kullback–Leibler 散度）的影响，另外来检查一下没有求和部分时的公式（3）。

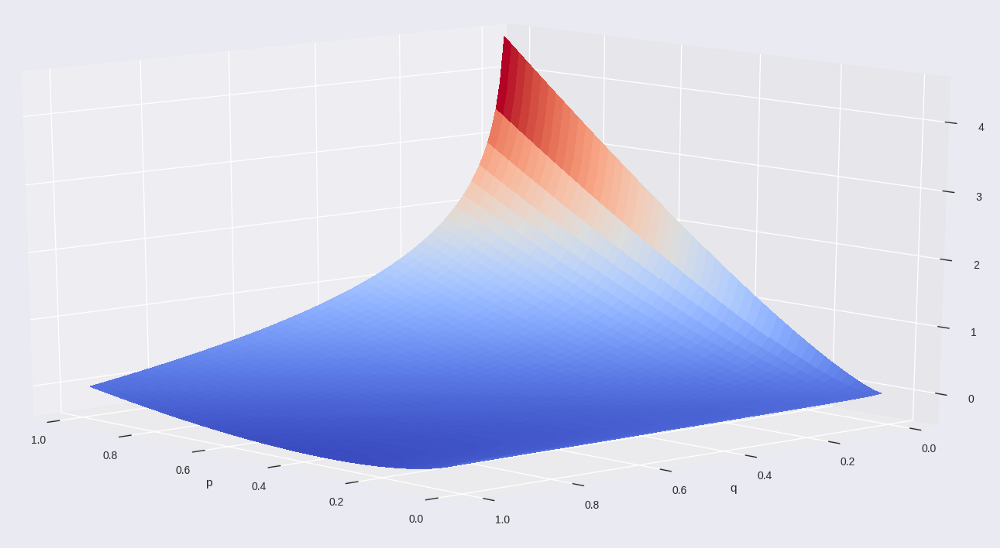
图 4 t-SNE 的不包括求和部分的损失函数

这很难理解，但是我确实把坐标轴的名字写在这里了。 可以看到，损失函数是非对称的。

当点在高维空间（p 轴）附近时，它会产生一个很大的代价值，但是却由低维度空间下的相距较远的点来表示，同样地，高维度空间下较远的点会产生较小的代价值，却由低维度空间下相距较近的点来表示。

这进一步说明了 t-SNE 绘制图的距离解释能力问题。

在鸢尾花数据集上使用 t-SNE 算法，看看在不同的复杂度下会发生什么

model = TSNE(learning_rate=100, n_components=2, random_state=0, perplexity=5)
tsne5 = model.fit_transform(iris_dataset.data)

model = TSNE(learning_rate=100, n_components=2, random_state=0, perplexity=30)
tsne30 = model.fit_transform(iris_dataset.data)

model = TSNE(learning_rate=100, n_components=2, random_state=0, perplexity=50)
tsne50 = model.fit_transform(iris_dataset.data)

plt.figure(1)
plt.subplot(311)
plt.scatter(tsne5[:, 0], tsne5[:, 1], c=colors)

plt.subplot(312)
plt.scatter(tsne30[:, 0], tsne30[:, 1], c=colors)

plt.subplot(313)
plt.scatter(tsne50[:, 0], tsne50[:, 1], c=colors)

plt.show()

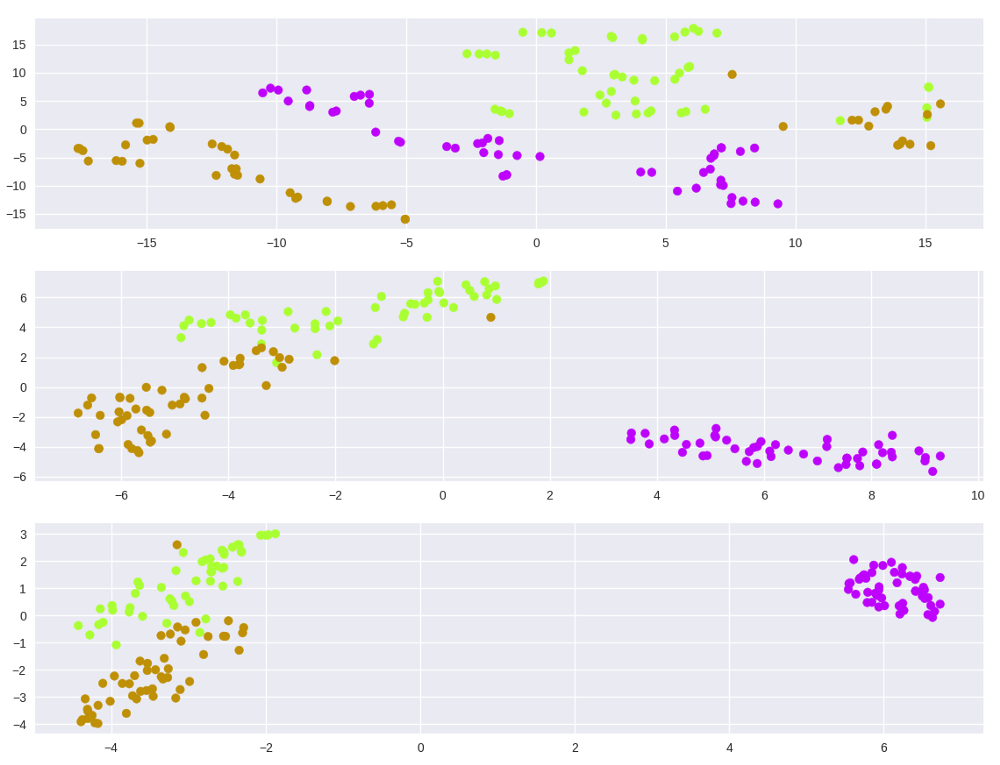
图 5 在鸢尾花数据集上使用 t-SNE 算法，不同的复杂度

正如我们从数学的角度理解的那样，可以看到，如果给定一个很好的复杂度的值，数据确实能够很好地聚类，同时请注意超参数的敏感性（如果不提供梯度下降的学习率，我们就无法找到该聚类）。

在我们继续之前，我想说，如果你能够正确地应用，那么 t-SNE 就是一个非常强大的方法，不要把你所学到的知识用到消极的一面上去，只要知道如何使用它即可。

接下来是自动编码器的内容。

自动编码器

PCA 和 t-SNE 是一种方法，而自动编码器则是一类方法。
自动编码器是一种神经网络，该网络的目标是通过使用更少的隐藏节点（编码器输出节点）来预测输入（训练该网络以输出与输入尽可能相似的结果），通过使用更少的隐藏节点（编码器输出节点）来编码与输入节点尽可能多的信息。

我们的 4 维鸢尾花数据集的自动编码器基本实现如图 6 所示，其中连接输入层和隐藏层的连线被称为“编码器”，隐藏层和输出层之间的连线被称为“解码器”。

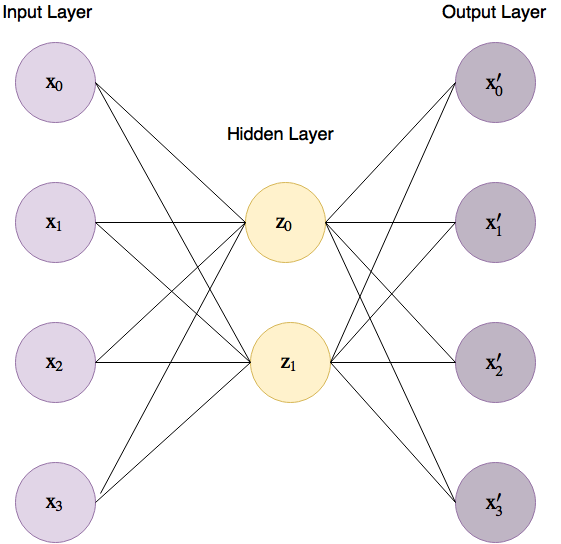
图 6 鸢尾花数据集上基础自动编码器结构

那么为什么自动编码器是是一个方法簇呢？因为我们唯一的限制是输入和输出层的相同维度，而在内部我们却可以创建任何我们想要使用的并能够最好地编码高维数据即可。

自动编码器从一些随机的低维表示法（z）开始，通过改变连接输入层和隐藏层，以及连接隐藏层和输出层的权重，并且使用梯度下降方法计算出最优的解决方案。

到目前为止，我们已经可以学习一些关于自动编码器的重要知识，因为我们控制着网络内部结构，所以我们可以设计编码器，使其能够选择特征之间非常复杂的关系。

自动编码器的另一个优点，是在训练结束时我们就得到了指向隐藏层的权重，我们可以对特定的输入进行训练，如果稍后我们遇到另外一个数据，我们可以使用这个权重来降低它的维数，而不需要重新训练 —— 但是需要小心，这样的方案只有在数据点与训练数据相似时才会有效。

在这种情况下，自动编码器的数学原理可能很简单，研究这个并不是很有用，因为我们选择的每个内部架构和成本函数的数学原理都是不同的。

但是如果我们花点时间想想如何优化自动编码器的权重，这样我们就会明白成本函数的定义有着非常重要的作用。

因为自动编码器会使用成本函数来决定它的预测的效果，所以我们可以使用这个能力来强调我们想要的。
无论我们想要欧几里德距离还是其它距离度量值，我们都可以通过成本函数将它反映到编码的数据上，使用不同的距离方法，使用对称和非对称函数等等。

更有说服力的是，由于自动编码器本质上是一个神经网络，我们甚至可以在训练时对类和样本进行加权，从而赋予数据中的某些现象更多的内涵。

这为我们压缩数据提供了很大的灵活性。

自动编码器非常强大，并且在某些情况下与其它方法（比如谷歌的“PCA 对自动编码器方法”）相比显示了一些非常好的结果，因此它们肯定是一种有效的方法。

让我们使用 TensorFlow 来实现一个基本的自动编码器，使用鸢尾花数据集来测试使用并绘制其图像

代码（自动编码器）

又一次，我们需要实现 fit 和 reduce 方法

def fit(self, n_dimensions):
    graph = tf.Graph()
    with graph.as_default():

        # 输入变量
        X = tf.placeholder(self.dtype, shape=(None, self.features.shape[1]))

        # 网络参数
        encoder_weights = tf.Variable(tf.random_normal(shape=(self.features.shape[1], n_dimensions)))
        encoder_bias = tf.Variable(tf.zeros(shape=[n_dimensions]))

        decoder_weights = tf.Variable(tf.random_normal(shape=(n_dimensions, self.features.shape[1])))
        decoder_bias = tf.Variable(tf.zeros(shape=[self.features.shape[1]]))

        # 编码部分
        encoding = tf.nn.sigmoid(tf.add(tf.matmul(X, encoder_weights), encoder_bias))

        # 解码部分
        predicted_x = tf.nn.sigmoid(tf.add(tf.matmul(encoding, decoder_weights), decoder_bias))

        # 以最小平方误差定义成本函数和优化器
        cost = tf.reduce_mean(tf.pow(tf.subtract(predicted_x, X), 2))
        optimizer = tf.train.AdamOptimizer().minimize(cost)

    with tf.Session(graph=graph) as session:
        # 初始化全局的变量参数
        session.run(tf.global_variables_initializer())

        for batch_x in batch_generator(self.features):
            self.encoder['weights'], self.encoder['bias'], _ = session.run([encoder_weights, encoder_bias, optimizer],
                                                                        feed_dict={X: batch_x})

这里没有什么特别之处，代码基本可以自解释，我们将编码器的权重保存在偏差中，这样我们就可以在接下来的 reduce 方法中减少数据。

def reduce(self):
    return np.add(np.matmul(self.features, self.encoder['weights']), self.encoder['bias'])

呵，就是这么简单 :)

让我们看看效果如何（批量大小为 50，1000 个轮次迭代）

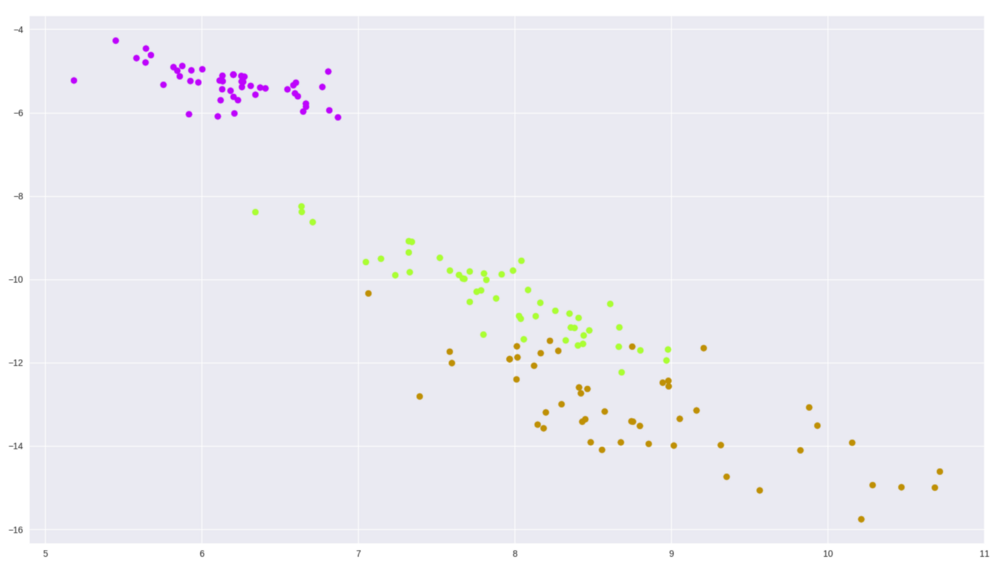
图 7 简单的自动编码器在鸢尾花数据集上的输出

即使不改变内部结构，我们使用不同的批量大小、轮次数量和不同的优化器等参数，也可能会得到不同的结果 —— 这只是刚刚开始的。

注意，我只是随机选择了一些超参数的值，在真实的场景中，我们将通过交叉验证或测试数据来衡量我们这么做的效果，并找到最佳的设置。

结语

像这样的帖文通常会以一些比较图表、优缺点等来结尾。 但这与我想要达到的目标恰恰相反。

我的目标是揭示这些方法的内部实现，这样读者就能理解每个方法的优缺点了。
我希望你能享受本次阅读，并且学到一些新的东西。

从文章的开头，到上面这三个问题，你现在感觉舒服多了吧？

如果发现译文存在错误或其他需要改进的地方，欢迎到 掘金翻译计划 对译文进行修改并 PR，也可获得相应奖励积分。文章开头的 本文永久链接 即为本文在 GitHub 上的 MarkDown 链接。

掘金翻译计划 是一个翻译优质互联网技术文章的社区，文章来源为 掘金 上的英文分享文章。内容覆盖 Android、iOS、前端、后端、区块链、产品、设计、人工智能等领域，想要查看更多优质译文请持续关注 掘金翻译计划、官方微博、知乎专栏。

avatar
文章
阅读
粉丝
相关推荐
常用的解决跨域问题的几种方法总结
234阅读
 · 
5点赞
浏览器窗口中几种常用的Observer
218阅读
 · 
3点赞
为什么 Bun 可能对 Node 降维打击？
13k阅读
 · 
104点赞
集合中的几种遍历方法
286阅读
 · 
1点赞
朱雀-前端部署的几种方式[三]
2.1k阅读
 · 
20点赞