写在前面
本文首发于公众号:符合预期的CoyPan
最近做了一个移动端活动页的需求,大概就是diy一个页面。用户可以对物料进行拖动、缩放、旋转,来达到diy的目的。用DOM来实现是不现实的,我采用了canvas来实现和用户的交互。开发过程中,涉及到了canvas中对物料元素的拖动、缩放、旋转等。本文将详细介绍在不使用任何第三方库的情况下,如何实现这些功能。最终的效果demo,可以参考上面的gif图。demo体验地址在这里:请用手机或浏览器模拟手机访问
本文先介绍整个需求中需要注意的数学知识。
需求分析
整个需求的大致流程是:
- 用户点击选择一个元素,则将该元素画在canvas中。
- 用户在canvas中对元素进行拖动、缩放、旋转等操作。
- 用户可以删除canvas中的某个元素。
在canvas中实现拖动、缩放、旋转等交互,最核心的两个点就是:
- 用户触摸时,判断用户是否触摸到了元素、是否触摸到了元素的缩放,旋转按钮。
- 用户移动手指时,根据手指的路劲,控制元素的运动。
我们知道,canvas中最基础的是坐标系统。本次的需求中,两个最关键的点是:
- 如何判断用户是否触摸到了某个元素,即触摸的落点问题。
- 如何通过坐标控制canvas中的元素的运动:移动、缩放、旋转。
落点问题:如何判断是否触摸到了某元素
首先提供一种简单的方法,canvas中有一个isPointInPath方法可以判断一个落点是否在某个路径中。不过如果canvas中的元素是图片,那么我们必须在画每一张图片时,为其加上一个路径包裹起来。这是一种解决落点问题的方案。这里不做深入介绍了,我采用的是下面的方案。
为了使问题简单化,可以大胆假设:
canvas中的所有元素(图片、各种图形等)都是长方形的。这已经能覆盖大部分情况了。长方形四个顶点的坐标就能确定一个元素的位置了。
而当用户触摸canvas时,通过触摸事件,可以拿到用户触摸的坐标。如果触摸坐标在长方形顶点坐标"内部",则表示触摸到了元素。于是,我们的问题可以抽象为:
已知长方形四个顶点坐标,某点的坐标,如何判断这个点是否在这个长方形内部。
如果长方形没有产生旋转,那么问题很简单,只用判断点的横纵坐标均在长方形的横纵坐标范围内即可。如果长方形产生了旋转,这种方法就没用了。要解决这个问题,先复习一下高中数学 。
向量
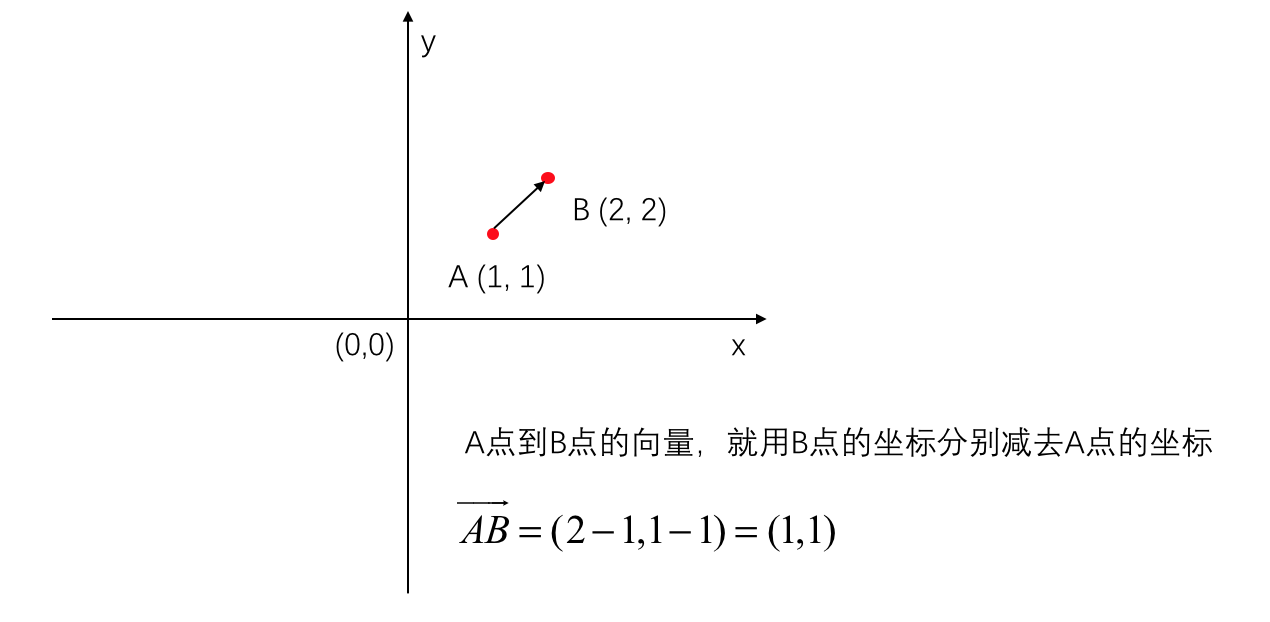
我们可以将二维平面上的坐标都转化为向量来计算,可以将问题简化很多。
向量的叉积
两个向量的叉积运算结果是一个向量而不是一个标量。叉积的方向与这两个向量所在的平面垂直。

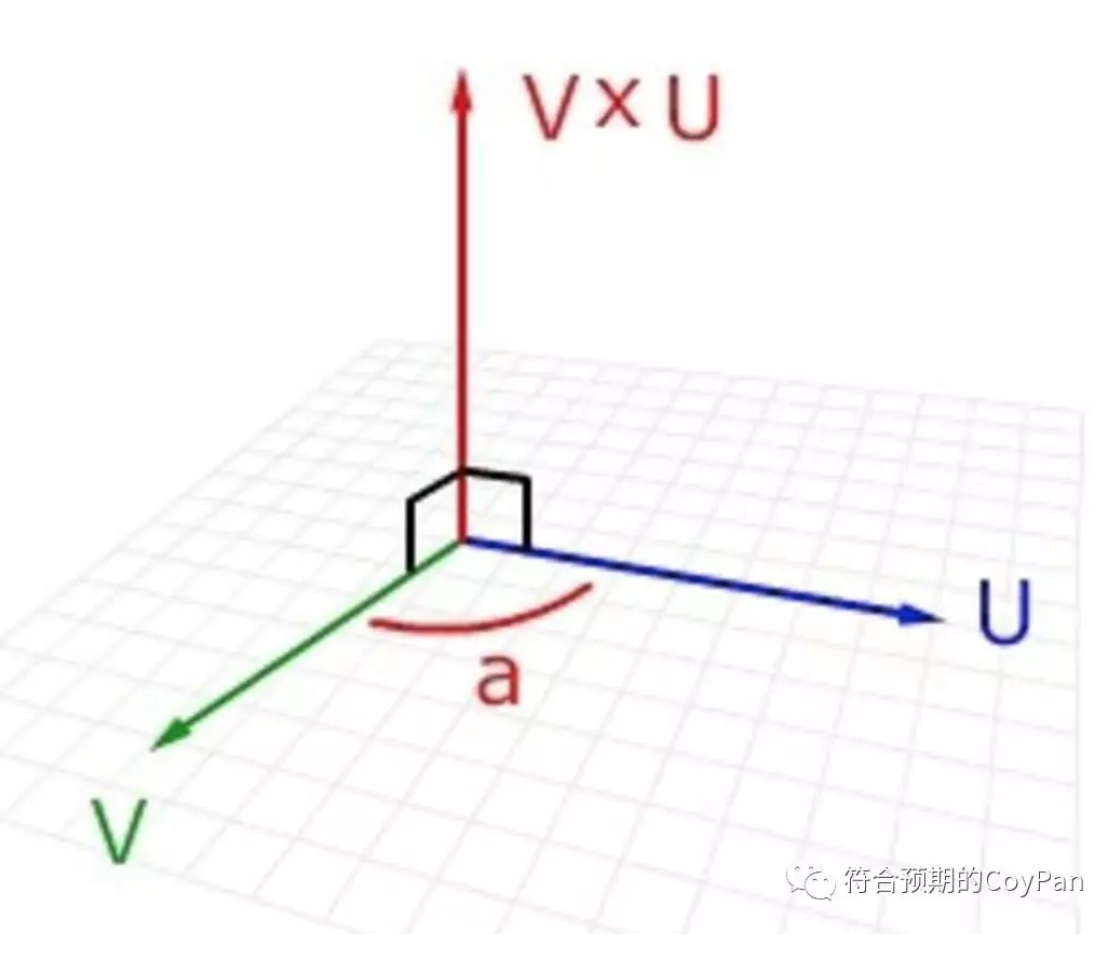

对于平面中的两个向量,第三维方向上的值都为0,其叉积的值为:

换句话说,我们可以很方便地判断:
一个平面中,在旋转角不超过180度的情况下,从一个向量到另外一个向量,是顺时针转动还是逆时针转动。
直接以canvas的二维坐标系统为例:
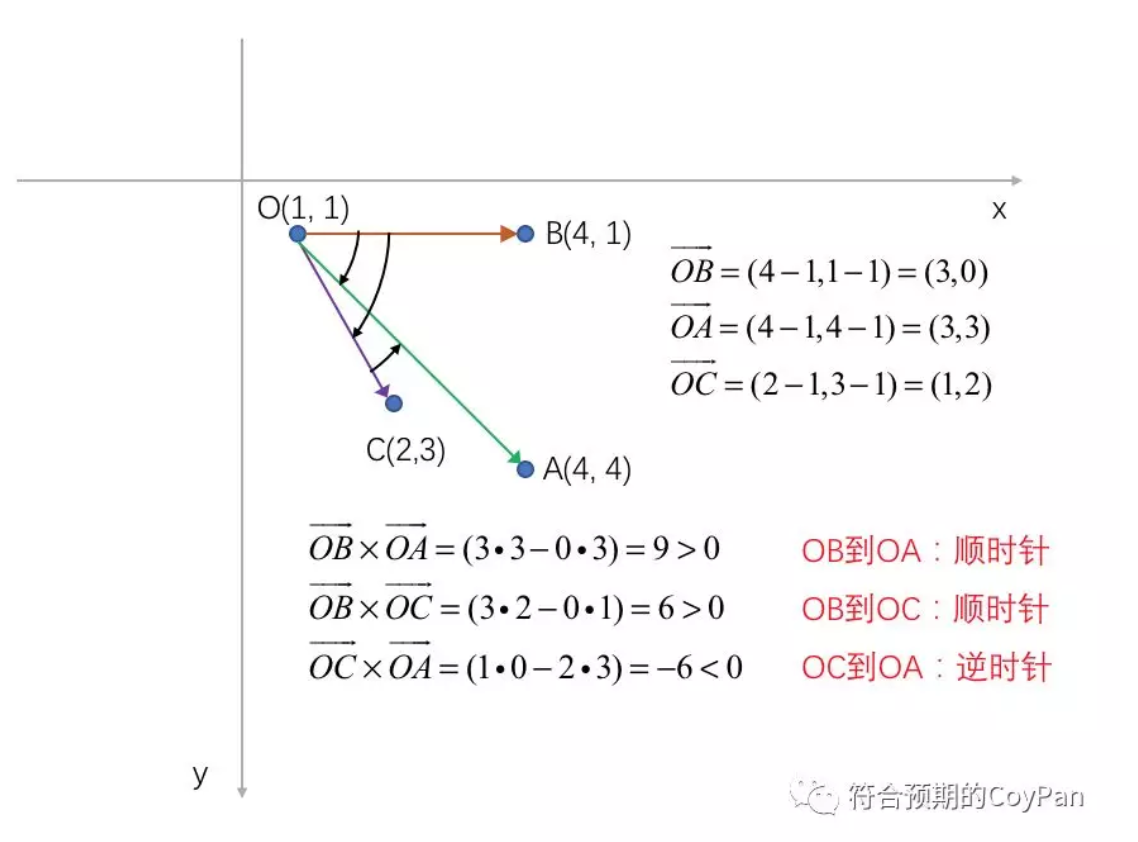
可以得到这样的结论:
在canvas二维平面中,设向量A与向量B的叉积对应的二项式的值为m。如果m>0,则向量A顺时针转动一个角度(小于180度),就能够到达向量B的方向。如果m<0,则需要逆时针转动。
判断落点在长方形内
落点在长方形内的情景如下:
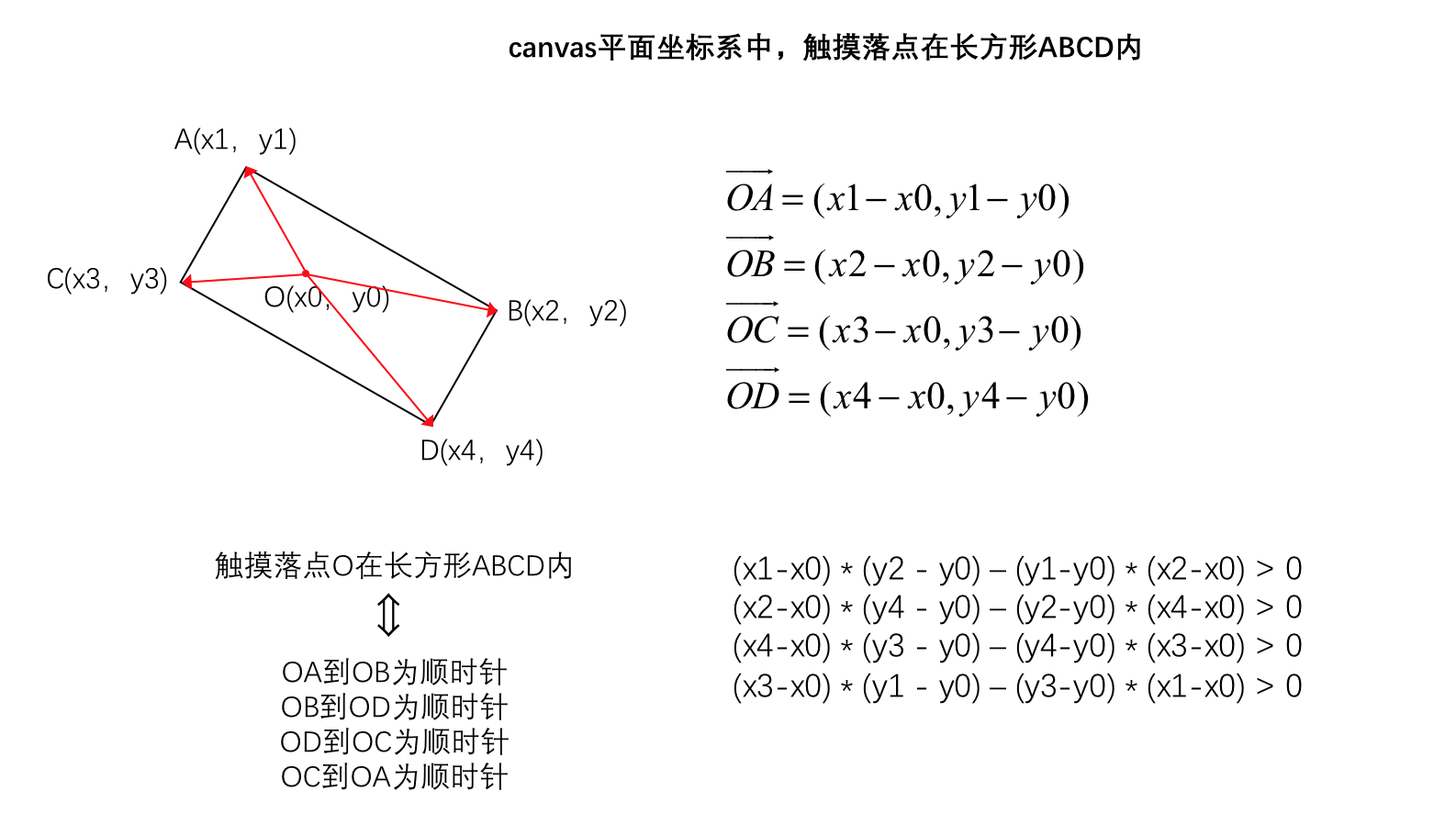
于是,判断【是否触摸到了canvas中某元素】的函数就有了:
/**
* 判断落点是否在长方形内
*
* @param {Array} point 落点坐标。 数组:[x, y]
* @param {Array} rect 长方形坐标, 按顺序分别是:左上、右上、左下、右下。
* 数组:[[x1, y1], [x2, y2], [x3, y3], [x4, y4]]
*
* @return {boolean}
*/
function isPointInRect(point, rect) {
const [touchX, touchY] = point;
// 长方形四个点的坐标
const [[x1, y1], [x2, y2], [x3, y3], [x4, y4]] = rect;
// 四个向量
const v1 = [x1 - touchX, y1 - touchY];
const v2 = [x2 - touchX, y2 - touchY];
const v3 = [x3 - touchX, y3 - touchY];
const v4 = [x4 - touchX, y4 - touchY];
if(
(v1[0] * v2[1] - v2[0] * v1[1]) > 0
&& (v2[0] * v4[1] - v4[0] * v2[1]) > 0
&& (v4[0] * v3[1] - v3[0] * v4[1]) > 0
&& (v3[0] * v1[1] - v1[0] * v3[1]) > 0
){
return true;
}
return false;
}
旋转角度
用户可以对canvas中的元素进行旋转,那么如何通过用户前后两次的触摸落点坐标求旋转角度呢?

从上面的等式可以看出,点积和叉积都能求夹角。选用哪一个呢?
在旋转的场景中,旋转的方向(逆时针or顺时针)是很重要的,而点积最终得到的只是一个标量,是没有方向。叉积是一个向量,是有方向的。我们选择叉积来计算旋转角度。
1、一般以canvas中的元素的中心为旋转原点,用户在canvas中触摸移动时,通过事件监听函数得到的前后两次触摸点的位移是很小的,与旋转中心形成的向量夹角必然是小于90度的。
2、向量的叉积正负值可以确定旋转方向。
3、反正弦函数是在负90度到90度之间单调递增的。
通过以上三点,可以得到:

于是,在canvas中,可以用以下函数来计算连续两次触摸落点与旋转中心形成的旋转角度:
/**
* 计算旋转角度
*
* @param {Array} centerPoint 旋转中心坐标
* @param {Array} startPoint 旋转起点
* @param {Array} endPoint 旋转终点
*
* @return {number} 旋转角度
*/
function getRotateAngle(centerPoint, startPoint, endPoint) {
const [centerX, centerY] = centerPoint;
const [rotateStartX, rotateStartY] = startPoint;
const [touchX, touchY] = endPoint;
// 两个向量
const v1 = [rotateStartX - centerX, rotateStartY - centerY];
const v2 = [touchX - centerX, touchY - centerY];
// 公式的分子
const numerator = v1[0] * v2[1] - v1[1] * v2[0];
// 公式的分母
const denominator = Math.sqrt(Math.pow(v1[0], 2) + Math.pow(v1[1], 2))
* Math.sqrt(Math.pow(v2[0], 2) + Math.pow(v2[1], 2));
const sin = numerator / denominator;
return Math.asin(sin);
}
已知旋转角度和初始坐标,求旋转后坐标
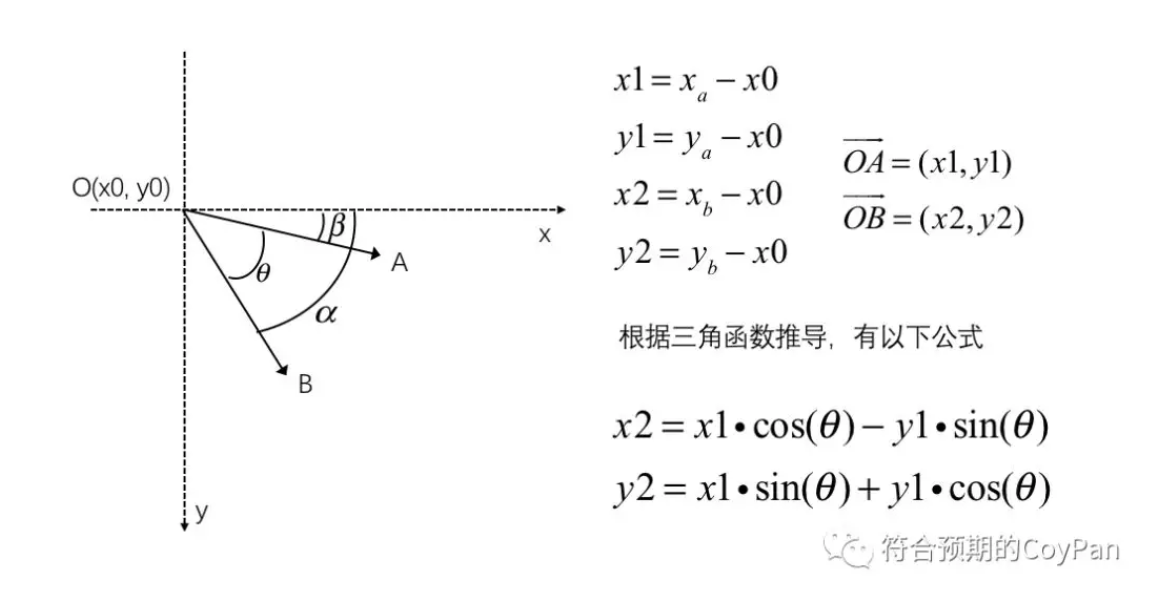
已知旋转起点、旋转中心以及旋转角度,求旋转终点坐标的函数如下:
/**
*
* 根据旋转起点、旋转中心和旋转角度计算旋转终点的坐标
*
* @param {Array} startPoint 起点坐标
* @param {Array} centerPoint 旋转点坐标
* @param {number} angle 旋转角度
*
* @return {Array} 旋转终点的坐标
*/
function getEndPointByRotate(startPoint, centerPoint, angle) {
const [centerX, centerY] = centerPoint;
const [x1, y1] = [startPoint[0] - centerX, startPoint[1] - centerY];
const x2 = x1 * Math.cos(angle) - y1 * Math.sin(angle);
const y2 = x1 * Math.sin(angle) + y1 * Math.cos(angle);
return [x2 + centerX, y2 + centerY];
}
拖拽、缩放
拖拽和缩放在本次需求中,对于数学上的要求并不高。 拖拽需要计算好触摸点横纵坐标的差值,加到canvas中的元素上即可。


写在后面
本文主要介绍了在canvas中实现拖拽、缩放、旋转等交互时,所需要的一些数学知识。如有不对的地方,欢迎指正。同时,如果有其他解决需求的思路,欢迎交流。
下一篇文章将介绍【使用本文介绍的数学知识,来实现文章开头的demo】的过程。
