对任意的可视化图形,都需要指定位置比例尺,也就是指定图形上数据所处的位置。如果我们不能将数据映射到位置——即使只是沿着坐标轴依次排列,那就谈不上数据可视化了。在常规的 2d 空间内,确定一个「点」的位置需要两个数据,因此我们需要两个的比例尺,通常情况下(但不一定)是 x 轴和 y 轴比例尺。我们还需要指定这些比例尺的相对几何排列。通常来说,x 轴是沿水平分布,而 y 轴则是沿着垂直方向,但我们也有其他选择。比如,我们可以让 y 轴相对于 x 轴某个角度分布,或者一个轴沿圆形(circle)分布,而另外一个轴沿径向(radial)分布。一组位置比例尺,和它们相对几何排列的组合就叫做坐标系(coordinate system)。
3.1 笛卡尔坐标系
使用作为广泛的可视化坐标系就是 2d 笛卡尔坐标系(2d Cartesian coordinate system),其中每个点的位置都由 x 值和 y 值来决定。x 轴和 y 轴相互垂直分布,呈正交坐标系,数据值沿两轴间隔分布(图 3.1)。两轴都是基于位置呈连续型比例尺分布,可以用来标示正负实数。要完全应用坐标系的话,我们需要指定每个轴所覆盖的输出范围(range)。在图 3.2 中,x 轴的 range 是 -2.2 到 3.2,而 y 轴是 -2.2 到 2.2。range 限制了只有落在这个区域中间的点才会被展示,range 之外的数据都会无法显示。
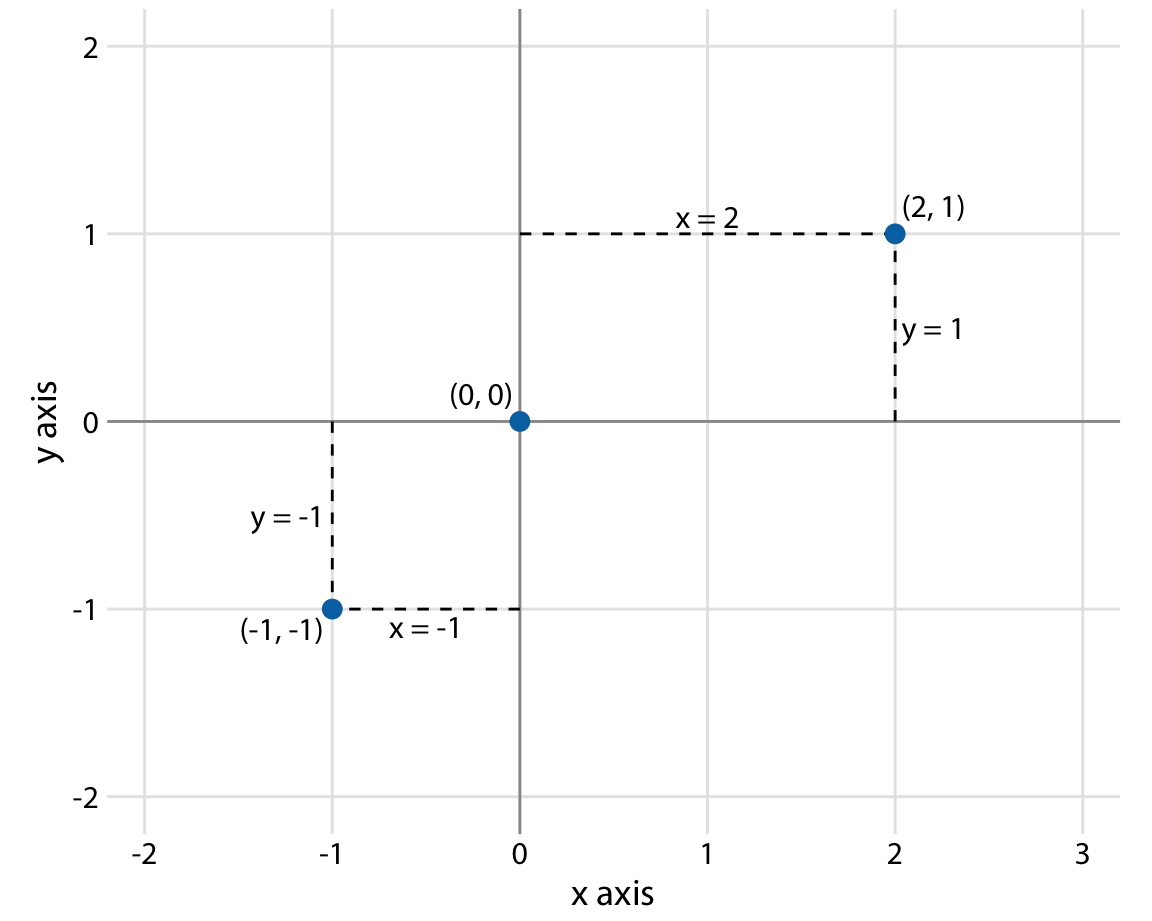
图 3.1:一个标准的笛卡尔坐标系。通常水平方向坐标轴称为 x 轴,而垂直方向为 y 轴,两轴交叉生成了等距间隔的网格系统。图例中 x 和 y 轴网格线都按照 1 个单元分隔,点(2, 1)x 轴距离原点右侧 2 个单位,y 轴距离原点上方 1 个单位。而点(-1, -1)距离原点左侧 1 个单位,下方 1 个单位。
通常数据不仅仅是纯数字类型的,而是自带「单位」的。举例来说,要测量温度,需要确认是摄氏度(℃)还是华氏度(℉);要测量距离,那么单位是公里还是英里,要测量时间,到底是分钟、小时还是天呢?在笛卡尔坐标系中,网格线之间的沿着坐标轴方向的间距对应的就是这些单位之间的离散间隔。以温度比例尺为例,我们可以每隔10℉ 设置一条网格线,如果是距离的比例尺,我们可以每隔 5KM 设置一条网格线。
笛卡尔坐标系中通常会两条坐标轴代表两类数据单元,很自然的,我们可以将两类变量分别映射到 x 轴 和 y轴。在图 2.3 中,我们绘制了一年中 温度 vs 月份的图表,其中 y 轴代表了华氏温度,每隔 20℉ 绘制一条网格线,x 轴 代表月份,每隔 3 个月绘制一条网格线。不论坐标轴代表了哪些不同的数据单元,我们可以相对于某一条坐标轴对另外一条做压缩或者拉伸,同时保持有效的数据可视化(图 3.2)。哪种图表类型更加合适取决于想对外传递的信息,高且窄的图形强调了 y 轴的变化趋势,短而宽的图形则相反。理想情况是:我们希望选择一个合适的宽高比,以确保任何位置上的重要差异都是显而易见的。
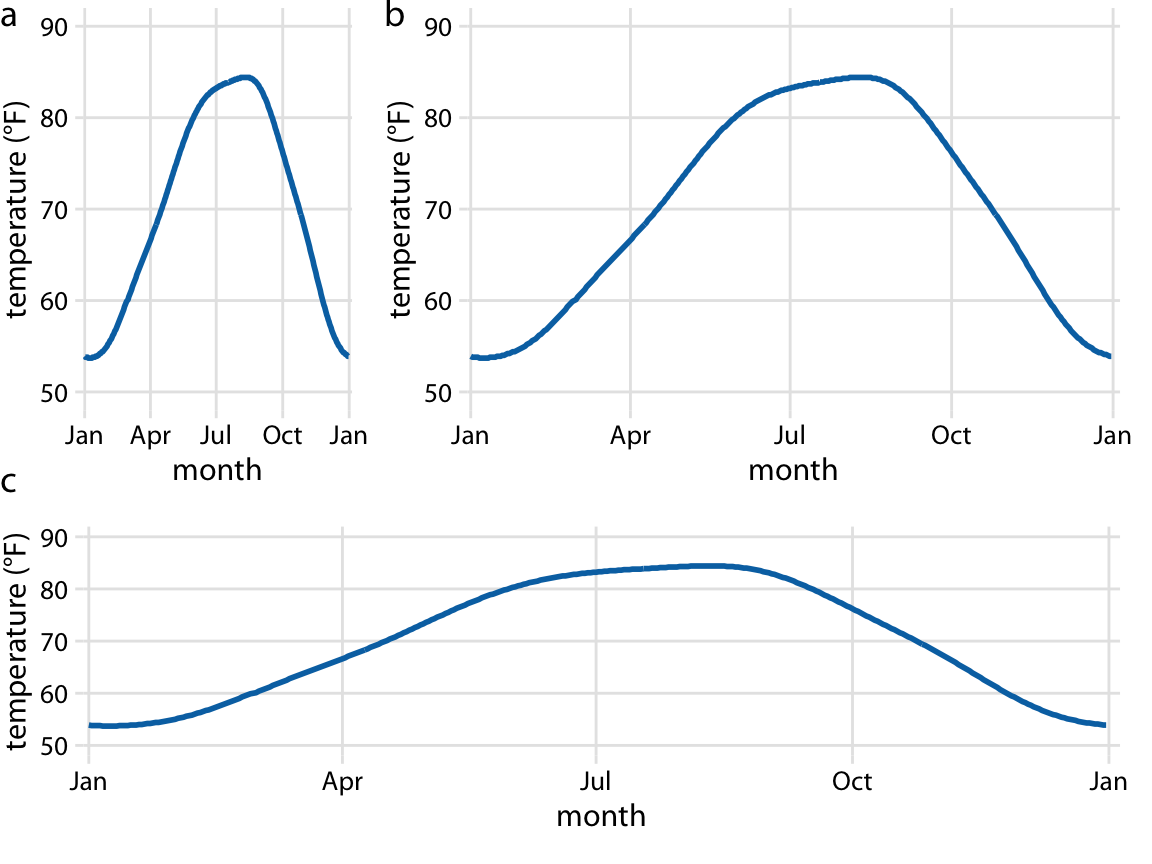
图3.2:Houston 日均温度变化趋势图。温度映射到 y 轴,日期则映射到 x 轴。 图(a), (b), (c) 三部分都是一样的数据,但是分别投射在不同宽高比的范围内。这三部分都是有效的数据可视化案例(取决于想传递的信息)。
还有一种场景是,如果 x 轴和 y 轴 代表的同一个数据单元,那么两条轴网格线的间距必须是完全相等的,因为此时沿着坐标轴方向的网格间距代表了同样大小的数据。图 3.3 中,x 轴 和 y 轴分别代表两个城市一年内温度随日期的变化趋势,我们需要保证沿着两条坐标轴方向数据是完全一样的,所以两个方向的网格线间距也是完全一致的,网格线之间就交叉形成了正方形。
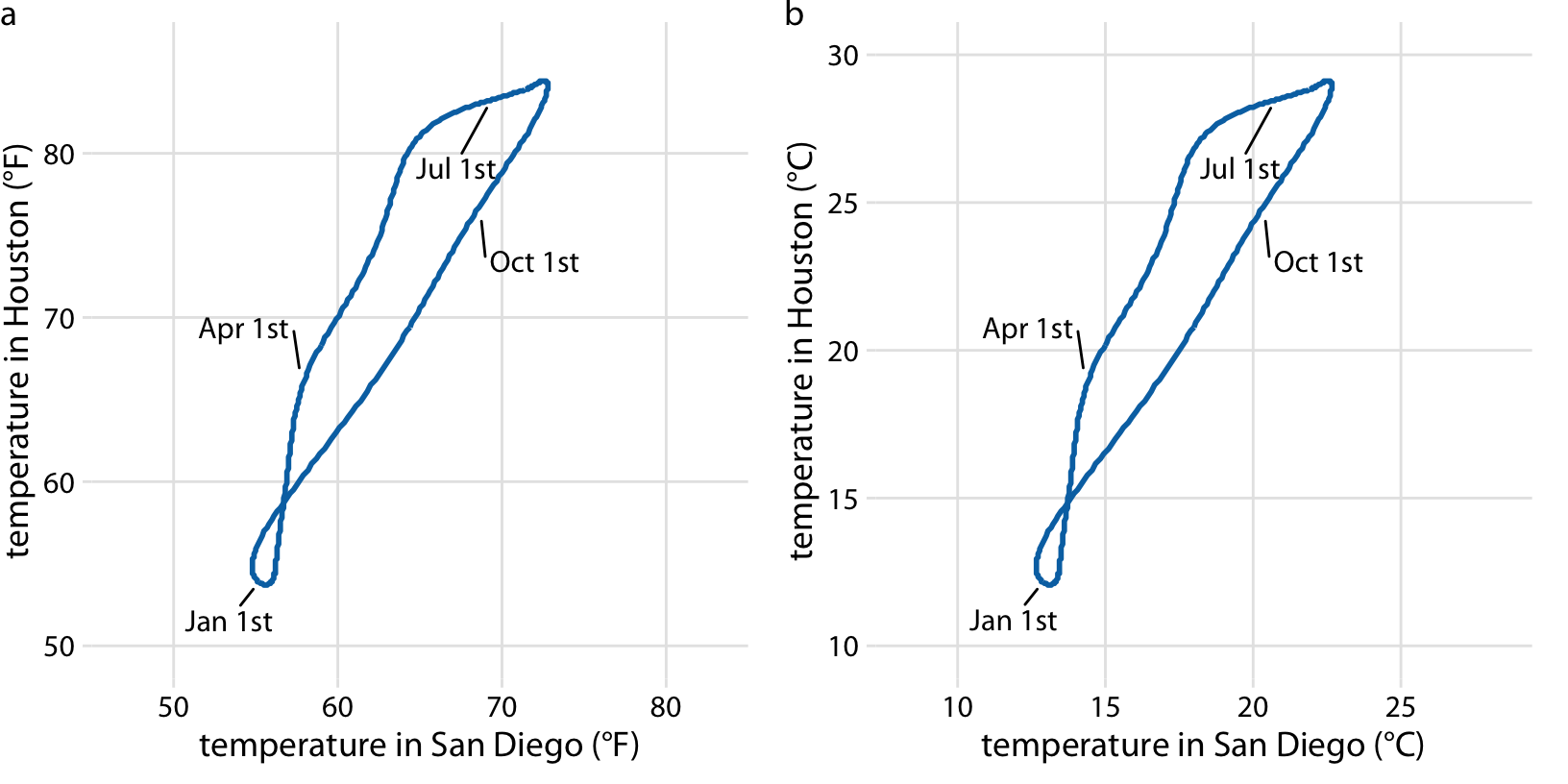
图 3.3:Houston 和 San Diego 每日温度对比图,其中 1月、4月、7月和10月的 1 号都添加了辅助标记。(a) 图展示华氏摄氏度,(b)图展示摄氏度。
你可能会好奇,如果修改了坐标轴的数据单元会怎么样,毕竟每个人都可能偏好不同的单位类型。修改数据单元是一种线性变换(linear transformation),基于原来的数据单元进行数据的相加、相减或相乘。幸运的是,笛卡尔坐标系在这种线性变换下是不会变化的,只要对坐标轴进行相应的修改,图形就不会改变。在图 3.3 中,(a)图和(b)图显示同一组数据,但是(b)图展示摄氏度,而(a)图展示华氏度,即使网格线的位置和间距不同,但两个图表看上去完全一致。
3.2 非线性坐标轴
在笛卡尔坐标系中,沿着坐标轴分布的网格线不管是按照数据单元,还是实际位置都是均匀分布的。我们将这种位置比例尺(position scale)称为线性的(linear)。线性比例尺能够准确无误地呈现数据,尽管如此,某些场景下我们非线性比例尺也会被优先考虑。非线性比例尺中,均匀分布的数据单元可能会对应到不均匀的位置间距,或者相反,均匀间隔的位置间距可能会对应到不均匀分布的数据单元。
最常见的非线性比例尺就是对数比例尺(log scale)。对数比例尺对乘法来说是线性的,这样的话每一个单位制就也就对应于上一个值乘以固定的数字(基数)。要创建一个对数比例尺,我们需要将原始数据进行对数转换后取幂值(exponentiate)并映射到坐标轴上。图 3.4 展示了这个转换过程,需要被转换的数据是 1,3.16,31.6 和 100。你可能会觉得数字 3.16 有些奇怪,实际上在对数比例尺中,3.16 是介于 1 和 10 之间的中间值,而 31.6 是介于 10 到 100 之间的中间值。从数学的角度来说:√10 ≈ 3.16,而 10^1.5 ≈ 31.6。
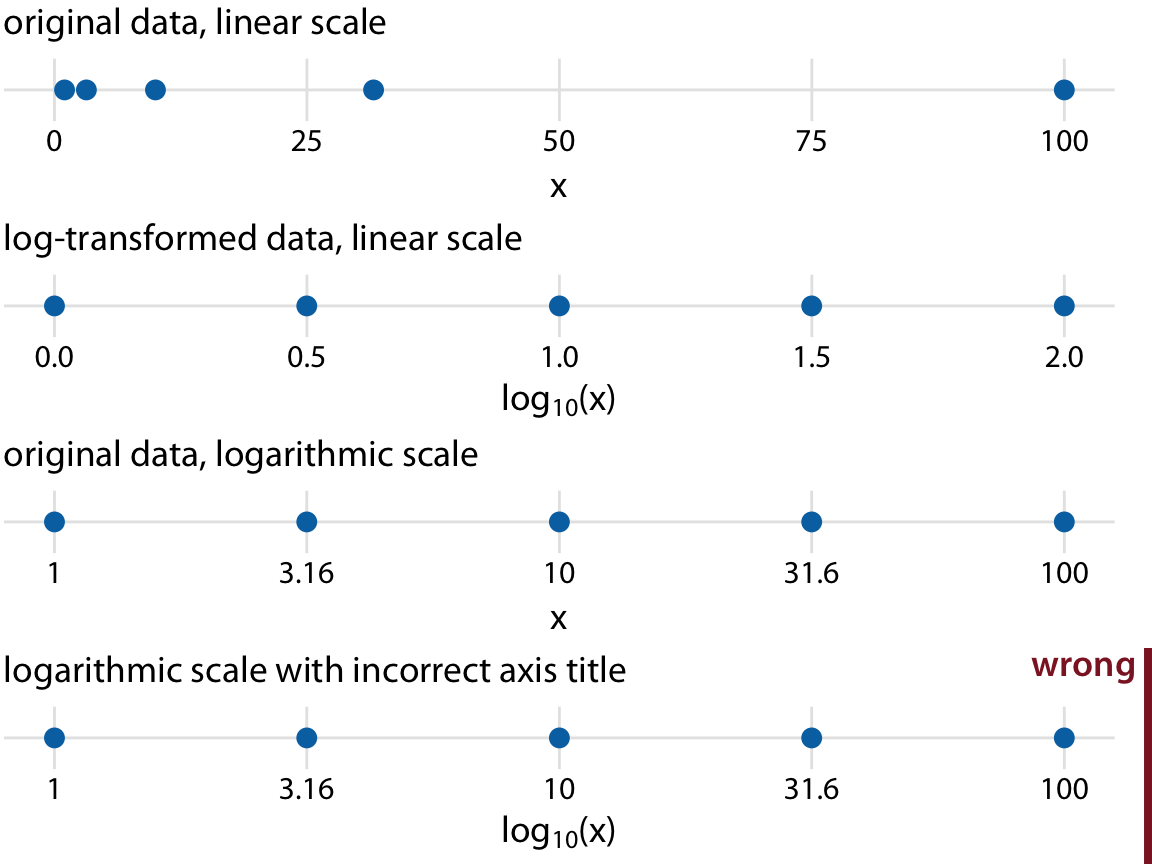
图 3.4:线性比例尺和对数比例尺之间的关系。数据 1,3.16,10,31.6,100 在线性比例尺上对应点的位置是均匀分布的。我们可以将原始数据直接映射到线性比例尺(最上方),也可以对数据进行对数转换后显示在线性比例尺(第 2 张),也可以直接将原始数据映射到对数比例尺(第 3 张)。值得一提的是,对数比例尺坐标轴 title 应该是原始变量,而不能是变量对数转换后的值(最后一张)。
在数学的角度,在线性比例尺上应用对数转换后的数据,和在对数比例尺上绘制原始数据没有什么不同(图 3.4),唯一的区别在于坐标轴的刻度。在大多数情况下,对数比例尺上的刻度标记是更优的选择,因为读者可以直观地看到原始数据,而不用面临着去做二次计算的压力。同样的,对数比例尺也可以减少读者对对数基数混淆的风险。当我们处理对数数据时,我们可能会对使用自然对数(e)还是基于 10 的对数感到困惑。含糊不清的标记一点都不罕见,以 “log(x)” 为例,它根本没有指定对数基数!我的建议是,在处理对数转换时始终指定基数,在绘制对数转换后的数据时,在坐标轴标签上始终指定基数。
对数比例尺上数据相乘看上去就像线性比例尺上数据的相加,所以对数比例尺天然适合于经过乘法、除法处理的数据,值得一提的是,对数的比例值需要展示在对数比例尺上。举例来说,我选取了得克萨斯州各县常驻居民数,并将其除以所有县的居民人数中位数。获取到的的结果是可能大于 1,也可能小于 1,如果恰好等于 1,那么所在县的人口数量就是中位数。我们将获取的值映射到对数比例尺上,我们可以清楚的看到得克萨斯州人口数量均匀地分布在中位数附近,并且人口最多的县比中位数多 100 倍左右,而最少的县比中位数少 100 倍左右(图 3.5)。相比之下,相同的数据在线性比例尺中,线性比例尺模糊了人口数量位于中位数的县和远低于中位数的县之间的差异(图 3.6)。
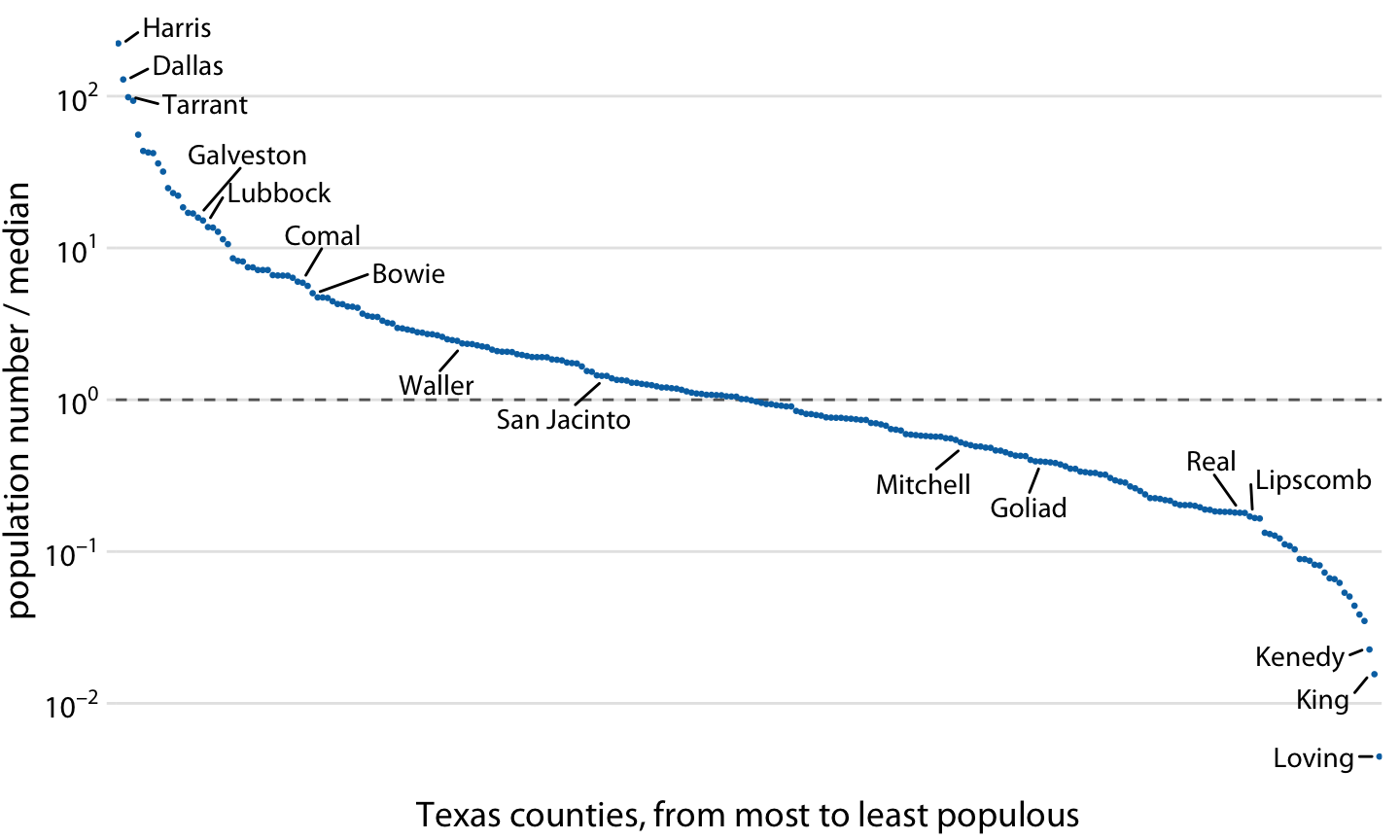
图 3.5:得克萨斯州各县人口数量相对于中位值(median),选中的县通过标签高亮显示。虚线代表中位值 1,对应全州人口数位于中位值的县。人口最多的县相比中位值大约多 100 倍,而人口最少的县比中位值少 100 倍左右。
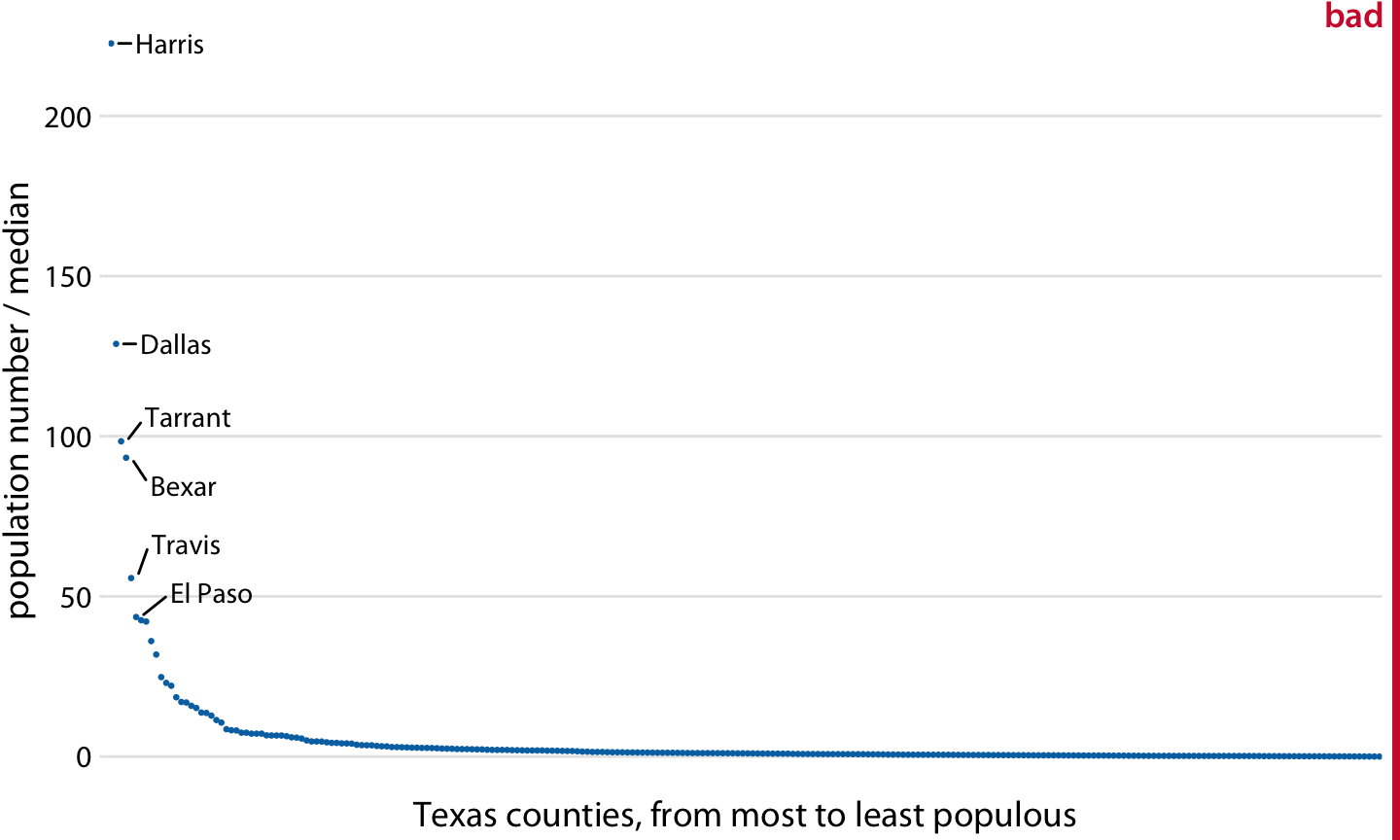
图 3.6:得克萨斯州各县人口数量相对于中位值(median)。在线性比例尺上,我们过分放大了 > 1 的比例,而忽视了 < 1的比例。一般来说,比例值不应该展示在线性比例尺上。
在对数比例尺上,数字 1 是一个天然的中间点,就像线性比例尺上的 0。可以理解为大于 1 的值是基于对数做乘法,而小于 1 的值是基于对数做除法。例如,我们可以这样写:10 = 1 * 10,而 0.1 = 1 / 10,数字 0 则永远不会出现在对数比例尺上,只会无限远离 1,可以理解为 log(0) = -∞,或者考虑从 1 到 0,需要除以无穷大才能趋近为 0(1 / ∞ = 0)。
对数比例尺适用于当数据集中的数据差异特别大时。对于图 3.5 和图 3.6 所示,人口最多的县(4,092,459)和最少的县(82)差异巨大,即使我们没有通过除以中位数转换为比例值,我们也应该考虑用对数比例尺来实现。但如果有一个人口数为 0 的县应该怎么做,这个时候我们无法直接用对数比例尺实现,因为log(0) 会无限趋近负无穷。这种时候,建议采用平方根(square root)进行数据转换。类似于对数比例尺,平方根比例尺也是将极大的数据压缩为较小的范围,只是允许存在 0。
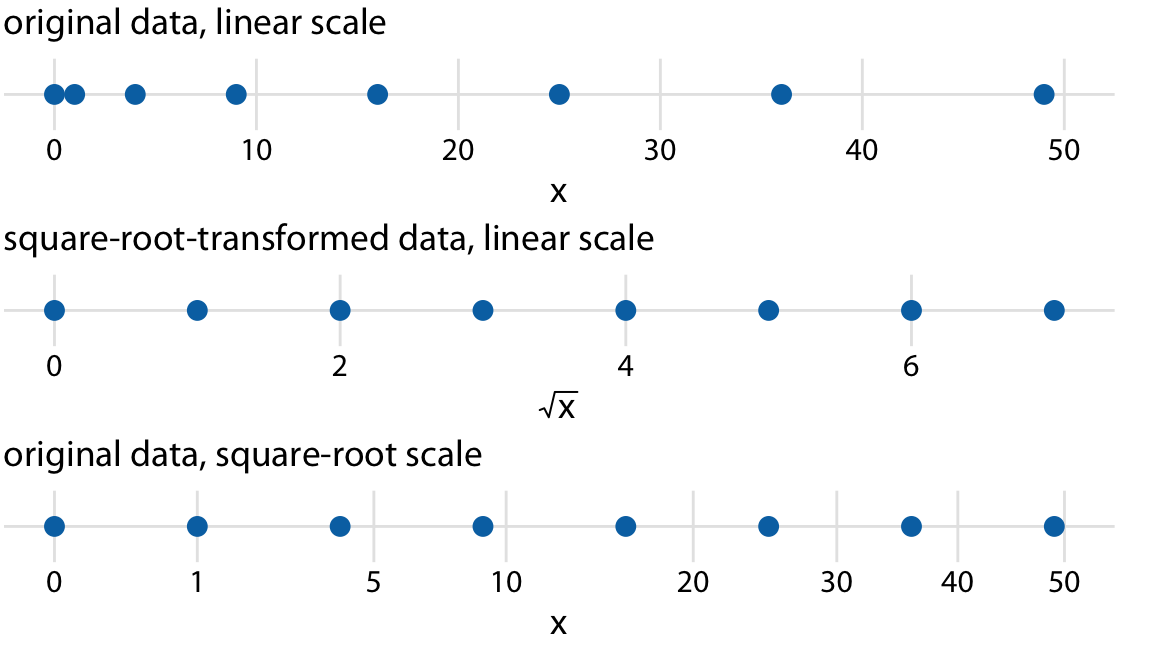
图 3.7:指数比例尺和平方根比例尺之间的关系。原始值 0, 1, 4, 9, 16, 25, 36, 49,在平方根比例尺上均匀分布,因为平方转换后的值就是 0 到 7。我们可以直接将原始值映射到线性比例尺上,也可以平方根转换后映射到线性比例尺上,最后也可以直接映射到平方根比例尺上。
我认为平方根比例尺存在两个问题。首先,在线性比例尺上每一个单位值对应于固定数值的加减操作,而对数比例尺上对应乘除操作,而平方根比例尺上不存在这样的规则,平方根比例尺上每一个单位值取决于开始时候的刻度值。其次,我们不清楚如何最优地将刻度分布在坐标轴上。为了获得均匀分布的网格,我们必须将它们放置在正方形上,但是每隔 1 个数字(0,4,16,36)的刻度分布会非常不直观,或者我们按照线性间隔(10,20,30,40)分布,但这样会导致在坐标轴低点标签(ticks)太少,而在高点标签太多。在图 3.7 中,我选择的方案是[0, 1, 5, 10, 20, 30, 40],这些值没有太多的逻辑,只是可以更合理地覆盖数据范围。
尽管平方根比例尺存在这些问题,但仍然是有效的位置比例尺,在某些场景下仍然有适用性。就像对数比例尺天然适合比率(ratio)一样,平方根比例尺仍然适合平方根处理的数据。有一个适合做平方根运算的场景是地理区域的面积处理。如果我们对地理区域的面积做平方根运算,我们可以获知该区域从北到南,或者从东到西的线性距离。如果我们想要知道在一个地区开车需要多长时间,这些范围可能是相关的。图 3.8 显示了美国东北部各州基于线性和平方根比例尺的面积值。尽管这些区域之间差异很大(图 3.8 a),但是决定开车时间的会更加靠近平方根比例尺上的数据(图3.8 b)。
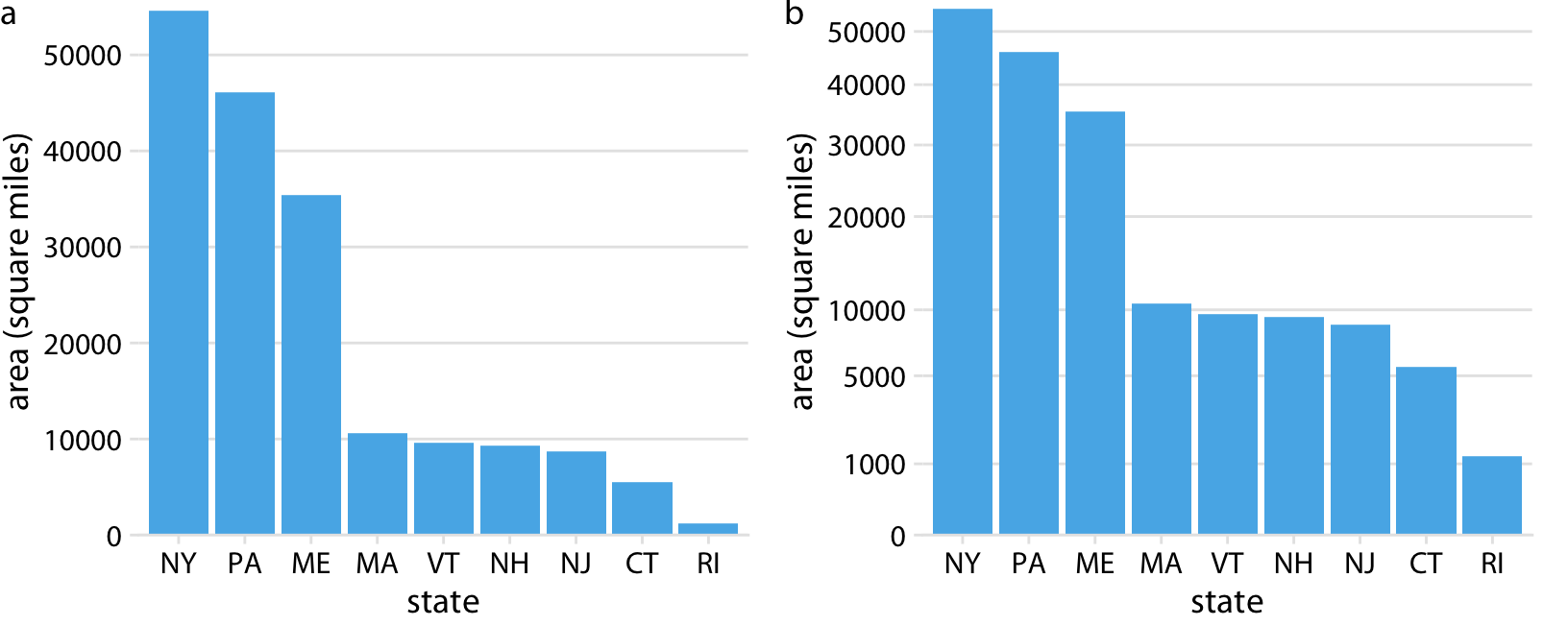
图 3.8:美国东北部各州的面积分布,(a)图基于线性比例尺,(b)图基于平方根比例尺。
3.3 坐标系和曲线坐标轴
目前我们所遇到的坐标系都是两个直线坐标轴之间以合适的角度连接,即使坐标轴建立的是非线性映射关系。除此以外,还有一类坐标系拥有曲线轴的坐标轴。例如在极坐标系(polar coordinate system)下,我们通过角度(angle)和径向距离(radial distance)来确定点的位置,因此角度坐标轴是环形的(图3.9)。
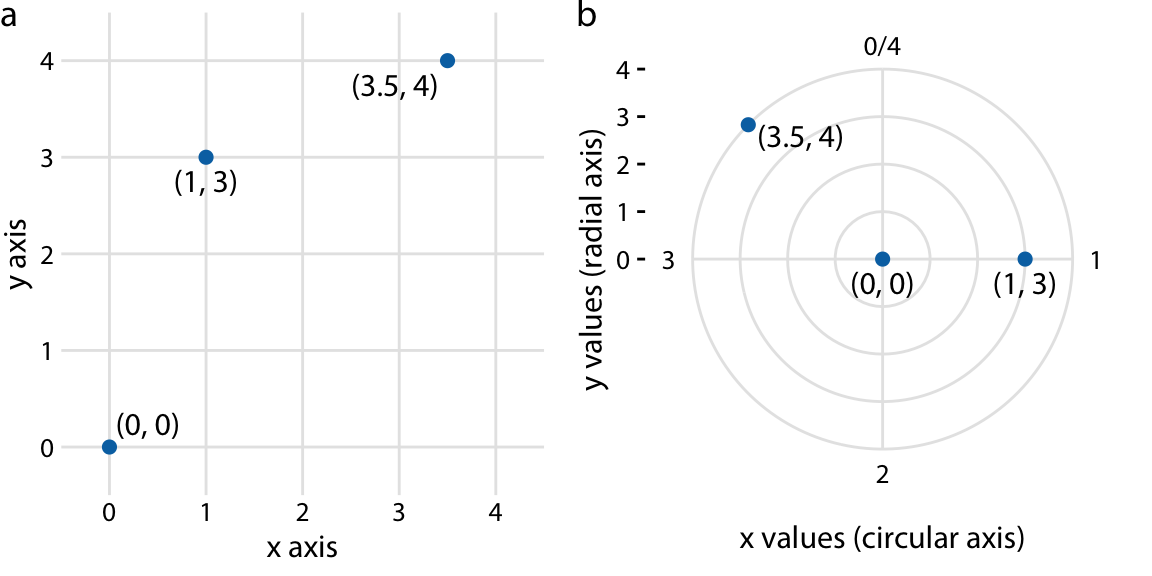
笛卡尔坐标系和极坐标系之间的关系。(a)笛卡尔坐标系上的三个点,(b)同样的三个点在极坐标上的位置。极坐标系中的角度轴对应于笛卡尔坐标系中的 x 轴,而径向轴则对应于 y 轴。这里环形角度轴对应的值是 0 到 4,因为环形的原因,0 和 4 是位于同一点上。
极坐标系适合于展示周期型的数据,使得数据集一端的值无缝连接到另一端的值。以一年的日期为例,12 月 31 日是一年的最后一天,同样是新年开始的前一天。如果我们要显示一年中某些变量的变化,在极坐标系上用角度轴来代表日期就比较合适了。让我们将这个概念应用到图 2.3 中的平均温度变化图。通过在极坐标系中绘制温度变化图,我们强调了温度随着日期变化的周期性(图3.10)。对比图 2.3,极坐标展系示了Houston、San Diego、Chicago 三个城市从 10月份到1月份之间气温是多么的接近,而在笛卡尔坐标系上,是很难得出这个结论的,此时12月和1月分别位于坐标轴的两个端,从视觉上是割裂的。
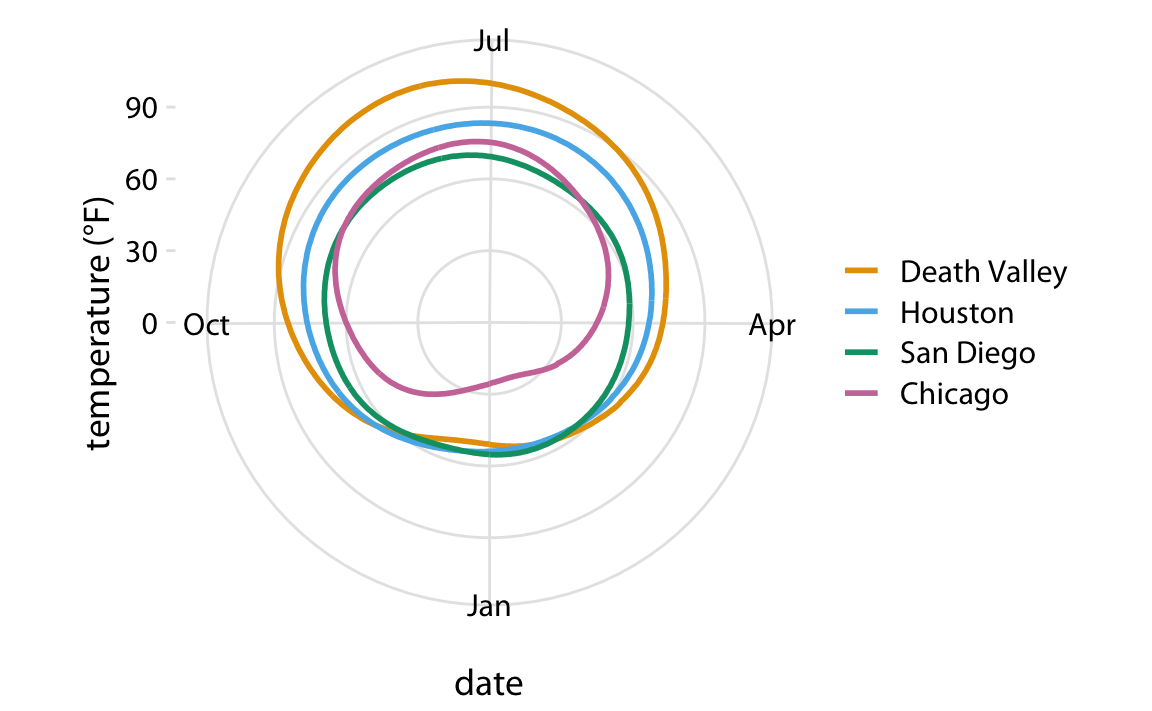
图3.10:美国四州每日温度变化图,以极坐标显示。距离中心点的径向距离代表华氏温度值,一年中的日期在 6 点钟开始逆时针排列。
第二类适合曲线轴展示的场景是地理数据展示,比如地图。地球上的位置是通过经度和纬度来确定的,但由于地球是一个球体,在笛卡尔坐标系上绘制是有误导性的,不推荐使用。相反,我们使用各种类型的非线性投影,试图最大限度地减少人工修饰。
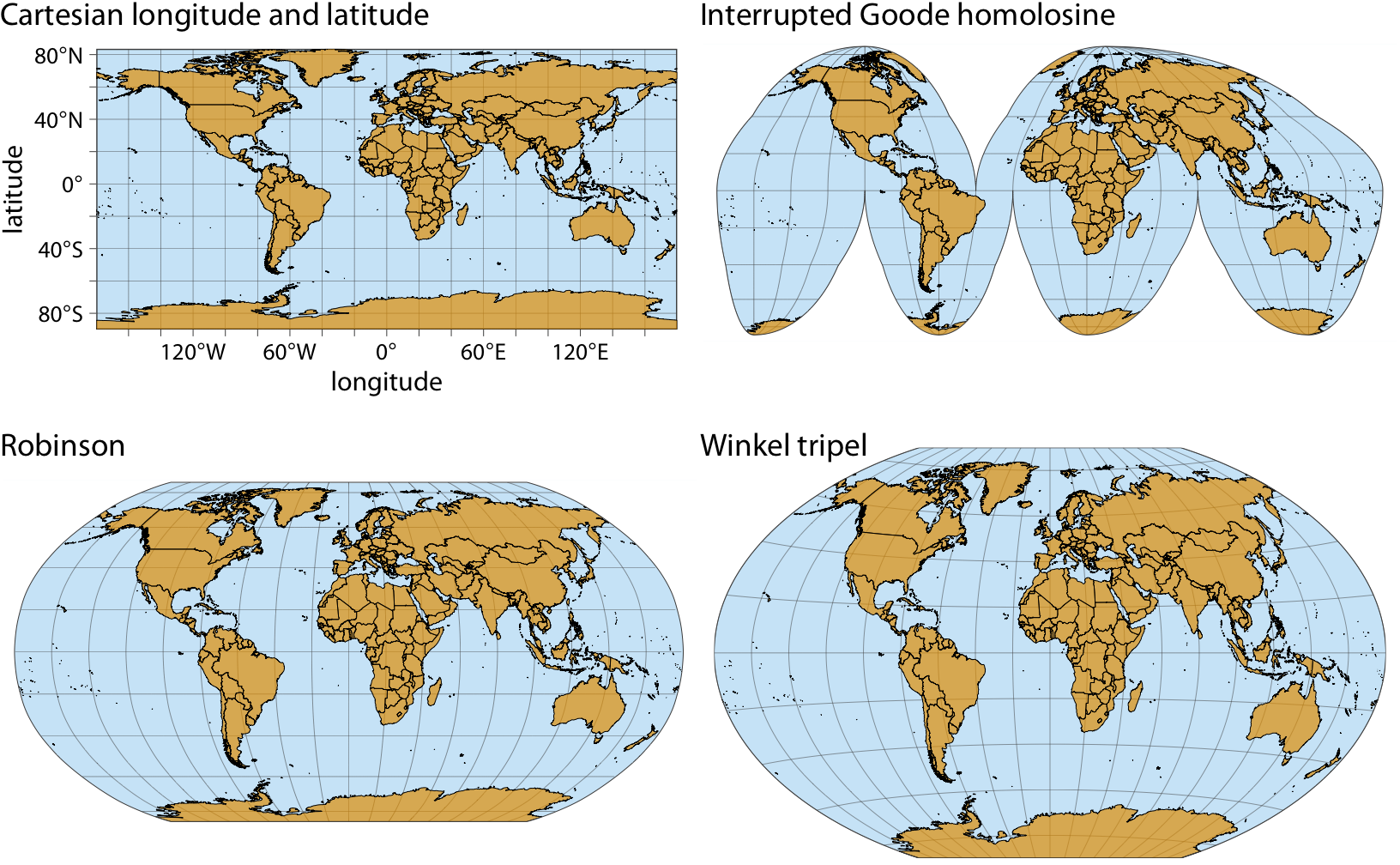
图3.11:四种不同类型的投影方式下的世界地图。笛卡尔坐标将每个位置的经纬度投射坐标轴上。这种映射关系导致在 3D 球体上其真实的面积和角度失真。interrupted Goode homolosine projection 投影则完美地代表了真实表面面积,代价是将一些陆地区域分成单独的部分,最著名的是格林兰岛和南极洲。Robinson 投影和 Winkel tripel 投影都是在角度和面积之间取得了平衡,他们通常都用于地图的全景。