[译] 时间序列的价格异常检测

原文地址：Time Series of Price Anomaly Detection

原文作者：Susan Li

译文出自：掘金翻译计划

本文永久链接：github.com/xitu/gold-m…

译者：kasheemlew

校对者：xionglong58，portandbridge

异常检测是指检测数据集中不遵循其他数据的统计规律的数据点

异常检测，也叫离群点检测，是数据挖掘中确定异常类型和异常出现的相关细节的过程。如今，自动化异常检测至关重要，因为现在的数据量太庞大了，人工标记已经不可能实现了。自动异常检测有着广泛的应用，例如反欺诈、系统监控、错误检测、传感器网络中的事件检测等等。

但我将对酒店房费进行异常检测，原因说起来有点自私。

不知道你是否有过这样的经历，比如，你定期到某地出差，每次下榻同一个酒店。通常情况下，房费的波动都不大。但是有些时候，即便还是同一个酒店的同一个房型都贵得吓人。由于出差补贴的限制，这时你就只能选择换一家酒店了。被坑了好几次之后，我开始考虑创建一个模型来自动检测这种价格异常。

当然，有些反常情况你一辈子只会遇到一次，我们可以提前知道，后面几年应该不会在同一时间再次碰上。比如 2019 年 2 月 2 日至 2 月 4 日亚特兰大惊人的房费。

在这篇文章中，我会尝试不同的异常检测技术，使用无监督学习对时间序列的酒店房费进行异常检测。下面我们开始吧！

数据

获取数据的过程很艰难，我只拿到了一些不够完美的数据。

我们要使用的数据是 Expedia 个性化酒店搜索数据的子集，点这里获取数据集。

我们将从 training.csv 中分割出一个子集：

选择数据点最多的酒店 property_id = 104517。
选择 visitor_location_country_id = 219（从另一段分析中可知国家号 219 代表美国）来统一 price_usd 列。这样做是因为各个国家在显示税费和房费上有不同的习惯，这个房费可能是每晚的费用也可能是总计的费用，但我们知道美国的酒店显示的就是每晚不含税费的价格。
选择 search_room_count = 1.
选择我们需要的其他特征：date_time、price_usd、srch_booking_window 和 srch_saturday_night_bool。

expedia = pd.read_csv('expedia_train.csv')
df = expedia.loc[expedia['prop_id'] == 104517]
df = df.loc[df['srch_room_count'] == 1]
df = df.loc[df['visitor_location_country_id'] == 219]
df = df[['date_time', 'price_usd', 'srch_booking_window', 'srch_saturday_night_bool']]

完成分割之后就能得到我们要使用的数据了：

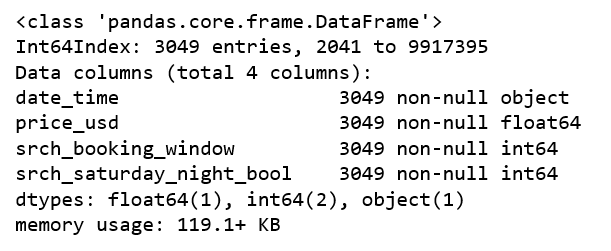
df.info()

df['price_usd'].describe()

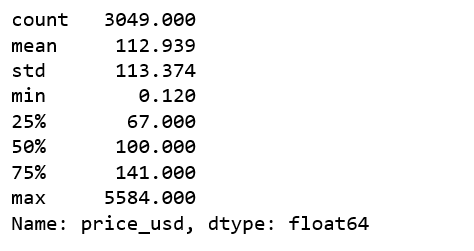
现在我们发现了一个严重的异常，price_usd 的最大值竟然是 5584。

如果一个单独的数据项与其他数据相比有些反常的话，我们就称它为单点异常（例如巨额交易）。我们可以检查日志，看看到底是怎么回事。经过一番调查，我觉得可能是数据错误，或者是某个用户无意间搜了一下总统套房，但是并没有预定或者浏览。为了发现更多比较轻微的异常，我决定删掉这条数据。

expedia.loc[(expedia['price_usd'] == 5584) & (expedia['visitor_location_country_id'] == 219)]

df = df.loc[df['price_usd'] < 5584]

看到这里，你一定已经发现我们漏掉了些条件，我们不知道用户搜索的房型，标准间的价格可是和海景大床房的价格大相径庭的。为了证明，请记住这一点。好了，该继续了。

时间序列可视化

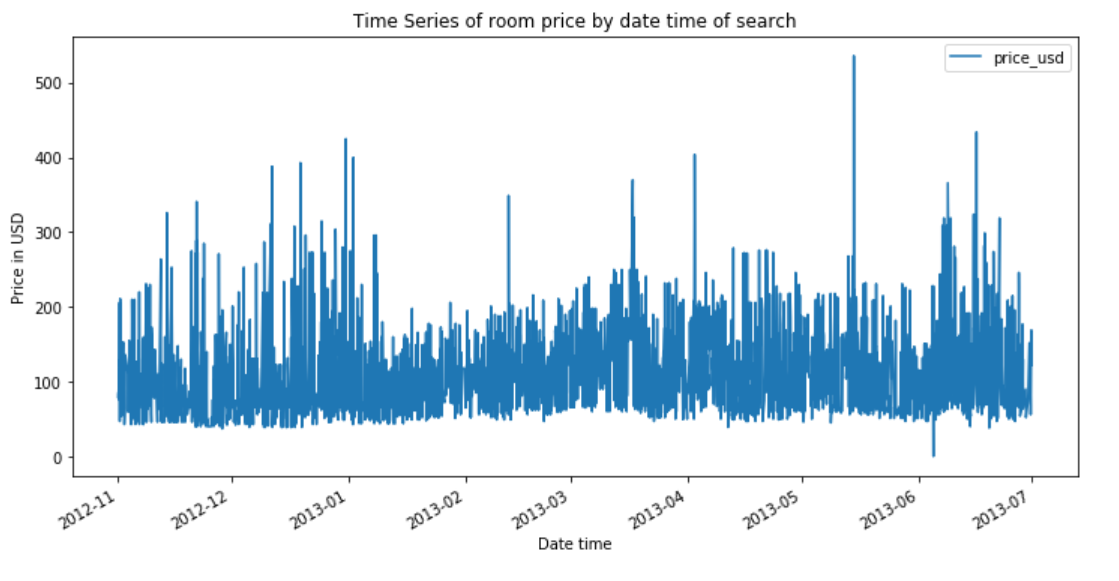
df.plot(x='date_time', y='price_usd', figsize=(12,6))
plt.xlabel('Date time')
plt.ylabel('Price in USD')
plt.title('Time Series of room price by date time of search');

a = df.loc[df['srch_saturday_night_bool'] == 0, 'price_usd']
b = df.loc[df['srch_saturday_night_bool'] == 1, 'price_usd']
plt.figure(figsize=(10, 6))
plt.hist(a, bins = 50, alpha=0.5, label='Search Non-Sat Night')
plt.hist(b, bins = 50, alpha=0.5, label='Search Sat Night')
plt.legend(loc='upper right')
plt.xlabel('Price')
plt.ylabel('Count')
plt.show();

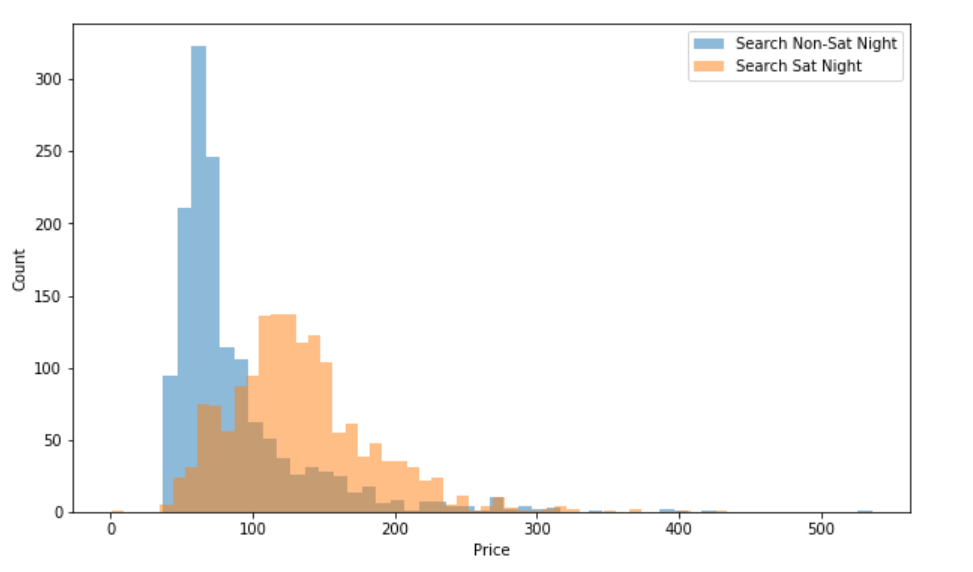
总的来说，搜索非周六的晚上得到的价格更加稳定和低廉，搜索周六晚上得到的价格明显上升。看来这家酒店周末的时候比较受欢迎。

基于聚类的异常检测

k-平均算法

k-平均是一个应用广泛的聚类算法。它创建 ‘k’ 个相似数据点簇。在这些聚类之外的数据项可能被标记为异常。在我们开始用 k-平均聚类之前，我们使用肘部法则来确定最优簇数。

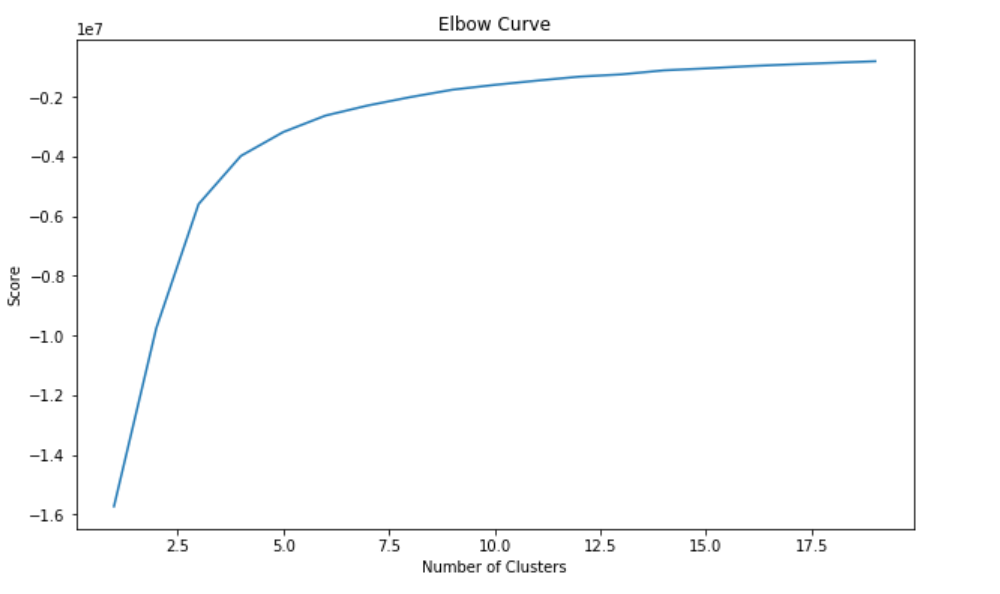
从上图的肘部曲线来看，我们发现图像在 10 个簇之后逐渐水平，也就是说增加更多的簇并不能解释相关变量更多的方差；这个例子中的相关变量是 price_usd。

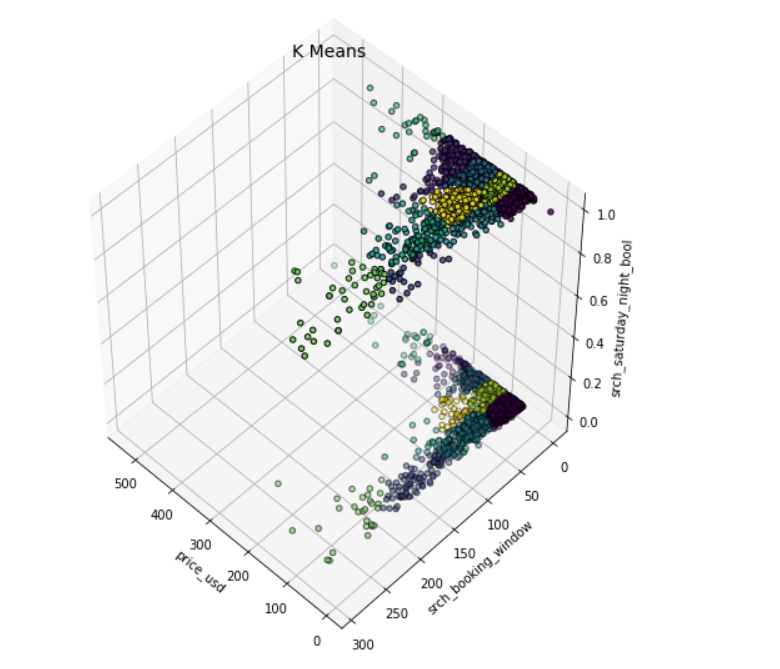
我们设置 n_clusters=10，使用 k-平均输出的数据绘制 3D 的簇。

现在我们得搞清楚要保留几个成分（特征）。

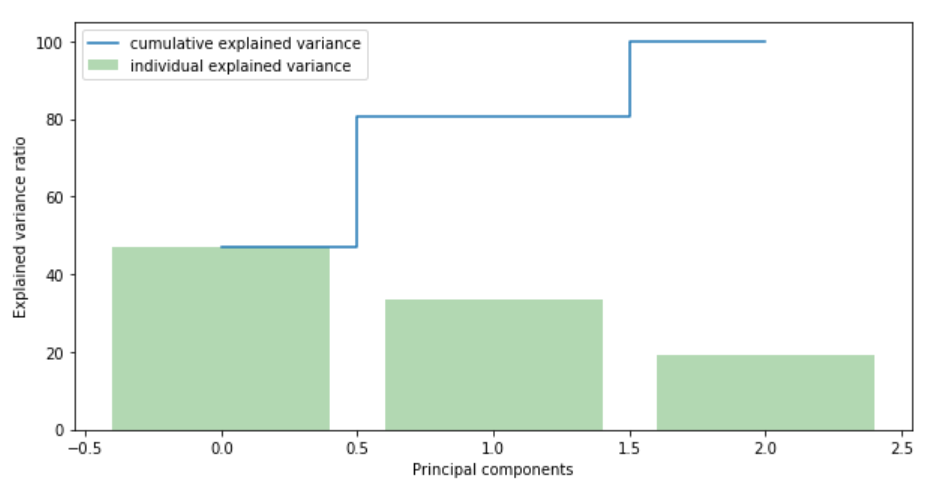
我们可以看到，第一个成分解释了解释了几乎 50% 的方差，第二个成分解释了超过 30% 的方差。然而，我们应该注意，没有哪一个成分是可以忽略不计的。前两个成分包含了超过 80% 的信息，所以我们设置 n_components=2。

基于聚类的异常检测中强调的假设是我们对数据聚类，正常的数据归属于簇，而异常不属于任何簇或者属于很小的簇。下面我们找出异常并进行可视化。

计算每个点和离它最近的聚类中心的距离。最大的那些距离就是异常。
我们用 outliers_fraction 给算法提供数据集中离群点比例的信息。不同的数据集情况可能不同，但是作为一个起点，我估计 outliers_fraction=0.01，这正是标准正态分布中，偏离均值的距离以 Z 分数的绝对值计超过 3 的观测值所占比例。
使用 outliers_fraction 计算 number_of_outliers 。
将 threshold 设置为离群点间的最短距离。
anomaly1 的异常结果包括上述方法的簇（0：正常，1：异常）。
使用集群视图可视化异常。
使用时序视图可视化异常。

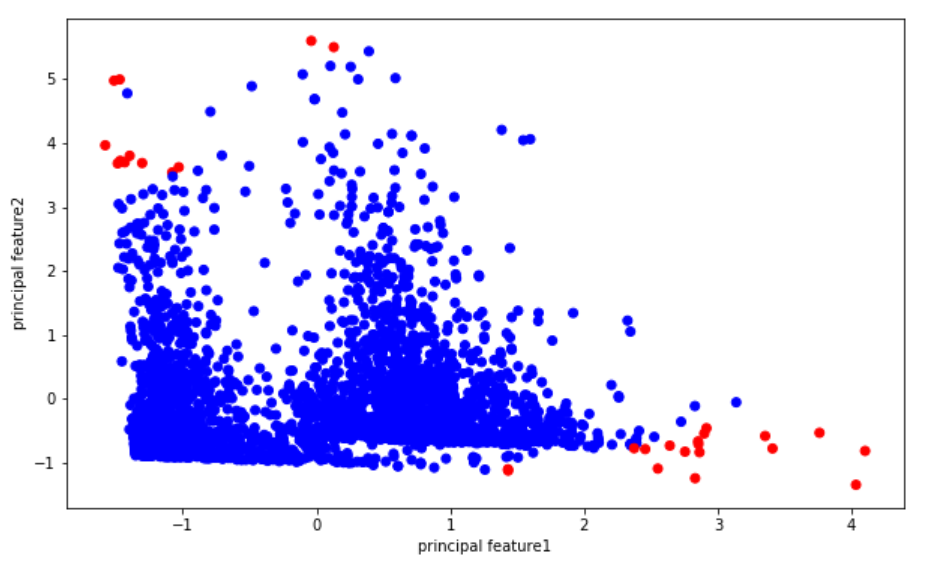
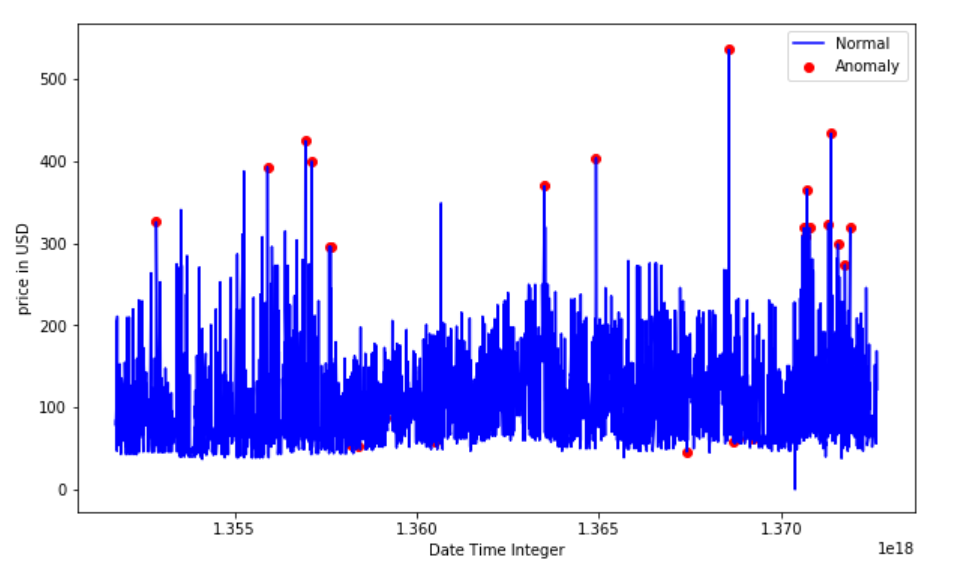
结果表明，k-平均聚类检测到的异常房费要么非常高，要么非常低。

使用孤立森林进行异常检测

孤立森林纯粹基于异常值的数量少且取值有异这一情况来进行检测。异常隔离不用度量任何距离或者密度就可以实现。这与基于聚类或者基于距离的算法完全不同。

我们使用一个IsolationForest模型，设置 contamination = outliers_fraction，这意味着数据集中异常的比例是 0.01。
fit 和 predict(data) 在数据集上执行异常检测，对于正常值返回 1，对于异常值返回 -1。
最终，我们得到了异常的时序视图。

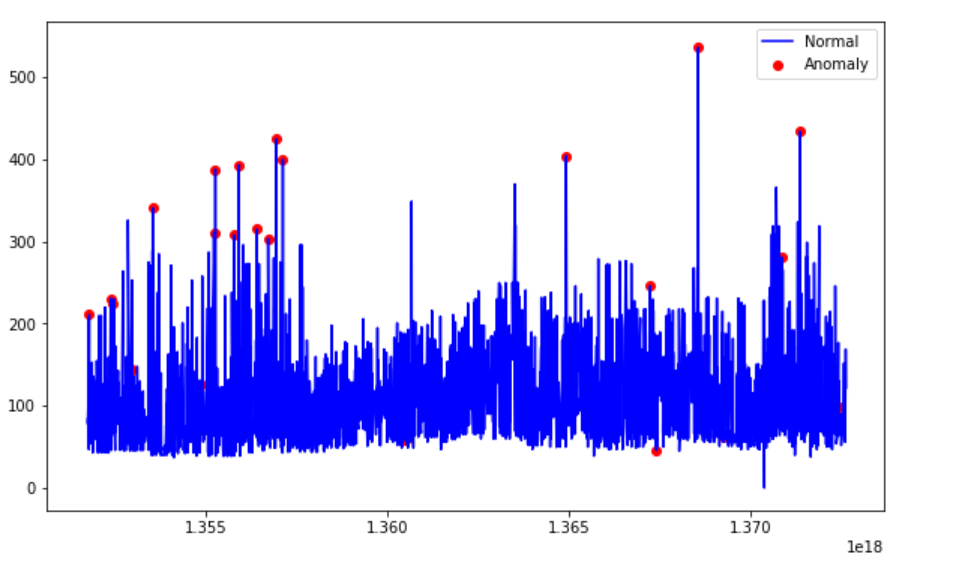
基于支持向量机的异常检测（SVM）

SVM 和监督学习紧密相连，但是 OneClassSVM 可以将异常检测当作一个无监督的问题，学得一个决策函数：将新数据归类为与训练数据集相似或者与训练数据集不同。

OneClassSVM

根据这篇论文： Support Vector Method for Novelty Detection。SVM 是基于间隔最大的方法，也就是不对一种概率分布建模。基于 SVM 的异常检测的核心就是找到一个函数，这个函数对于点密度高的区域输出正值，对于点密度低的区域返回负值。

在拟合 OneClassSVM 模型时，我们设置 nu=outliers_fraction，这是训练误差的上界和支持向量的下界，这个值必须在 0 到 1 之间。这基本上是我们预计数据里面的离群值占比多少。
指定算法中的核函数类型：rbf。此时 SVM 使用非线性函数将超空间映射到更高维度中。
gamma 是 RBF 内核类型的一个参数，控制着单个训练样本的影响 — 它影响着模型的"平滑度"。经过试验，我没发现什么重要的差别。
predict(data) 执行数据分类。因为我们的模型是一个单类模型，所以只会返回 +1 或者 -1，-1 代表异常，1 代表正常。

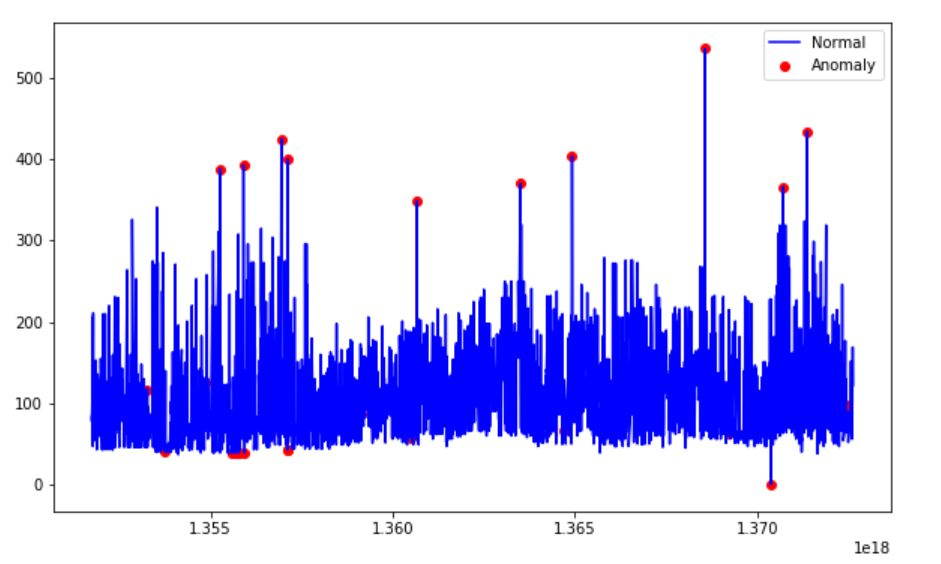
使用高斯分布进行异常检测

高斯分布又称为正态分布。我们将使用高斯分布开发一个异常检测算法，换言之，我们假设数据服从正态分布。这个假设并不适用于所有数据集，一旦成立，就能高效地确定离群点。

Scikit-Learn 的 [**covariance.EllipticEnvelope**](https://scikit-learn.org/stable/modules/generated/sklearn.covariance.EllipticEnvelope.html) 函数假设我们的全体数据是一概率分布的外在表现形式，其背后服从一项多变量高斯分布，以此尝试计算数据数据总体分布的关键参数。过程类似这样：

根据之前定义的类别创建两个不同的数据集 —— search_Sat_night、Search_Non_Sat_night。
对每个类别使用 EllipticEnvelope（高斯分布）。
我们设置 contamination 参数，它是数据集中出现的离群点的比例。
我们用 decision_function 来计算给定观测值的决策函数，它和平移马氏距离等价。为了确保和其他离群点检测算法的兼容性，成为离群点的阈值被设置为 0。
predict(X_train) 使用拟合好的模型预测 X_train 的标签（1 表示正常，-1 表示异常）。

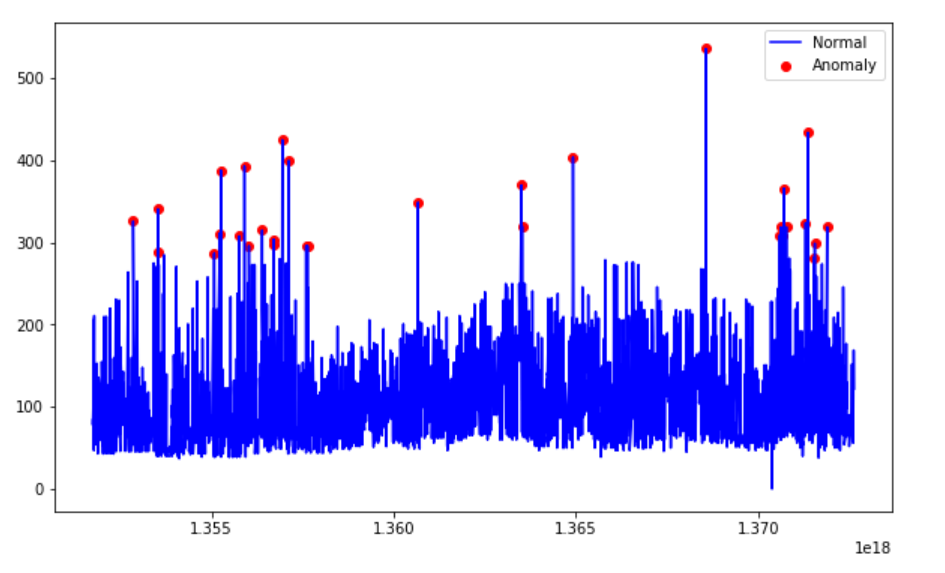
有趣的是，这种方式检测只检测到了异常高的价格，却没有检测到异常低的价格。

目前为止，我们已经用四种方法完成了价格异常检测。因为我们是用无监督学习进行异常检测的，建好模型之后，我们没什么可以用来对比测试，也就无法知道它的表现究竟如何。因此，在用这些方法处理关键问题之前必须对它们的结果进行测试。

Jupyter notebook 已经上传至 Github。好好享受这一周吧！

参考文献：

如果发现译文存在错误或其他需要改进的地方，欢迎到掘金翻译计划对译文进行修改并 PR，也可获得相应奖励积分。文章开头的 本文永久链接 即为本文在 GitHub 上的 MarkDown 链接。

掘金翻译计划是一个翻译优质互联网技术文章的社区，文章来源为掘金上的英文分享文章。内容覆盖 Android、iOS、前端、后端、区块链、产品、设计、人工智能等领域，想要查看更多优质译文请持续关注掘金翻译计划、官方微博、知乎专栏。