简介
本文介绍了常见的 10 种排序算法的原理、基本实现和常见的优化实现,并有(个人认为)足够详细的代码注释。
实在是居家工作,面试笔试必备良药。
这里只给出基于其原理的一般实现,很多算法都有逻辑更复杂的或代码量更少的精简版,像遍历的改成递归的,两个函数实现的改成一个函数等等,就不再提及了。
够详细了!傻子都能看懂!如果不懂,多看几遍!
前几天在微博上看到一个视频:用音频演示15种排序算法,可以看一下
所有动图均来自《十大经典排序算法总结(JavaScript 描述)》
分类
另一种分类方式是根据是否为“比较排序”。
- 常见比较排序:
- 冒泡排序
- 选择排序
- 插入排序
- 快速排序
- 归并排序
- 常见非比较排序:
- 计数排序
- 基数排序
- 桶排序
复杂度和稳定性
| 平均时间复杂度 | 最好 | 最坏 | 空间复杂度 | 稳定性 | |
|---|---|---|---|---|---|
| 冒泡排序 | O(n^2) | O(n) | O(n^2) | O(1) | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 堆排序 | O(n logn) | O(n logn) | O(n logn) | O(1) | 不稳定 |
| 插入排序 | O(n^2) | O(n) | O(n^2) | O(1) | 稳定 |
| 希尔排序 | O(n logn) | O(n log^2 n) | O(n log^2 n) | O(1) | 不稳定 |
| 快速排序 | O(n logn) | O(n logn) | O(n^2) | O(logn) | 不稳定 |
| 归并排序 | O(n logn) | O(n logn) | O(n logn) | O(n) | 稳定 |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(k) | 稳定 |
| 桶排序 | O(n+k) | O(n+k) | O(n^2) | O(n+k) | 稳定 |
| 基数排序 | O(n*k) | O(n*k) | O(n*k) | O(n+k) | 稳定 |
冒泡排序 Bubble Sort
一般实现
已排序元素将放在数组尾部
大致流程:
- 从第一个元素开始,比较每两个相邻元素,如果前者大,就交换位置
- 每次遍历结束,能够找到该次遍历过的元素中的最大值
- 如果还有没排序过的元素,继续1
演示图:
function bubbleSort(arr) {
for (let i = 0; i < arr.length - 1; i++) {
for (let j = 0; j < arr.length -1 - i; j++) {
if (arr[j] > arr[j+1]) swap(arr, j ,j+1)
}
}
return arr
}
// 后面还会多次用到,就不再写出来了
function swap(arr, n, m) {
[arr[n], arr[m]] = [arr[m], arr[n]]
}
有优化空间,主要从两方面进行优化:
- 减少外层遍历次数
- 让每次遍历能找到两个极值
优化1
检查某次内层遍历是否发生交换。
如果没有发生交换,说明已经排序完成,就算外层循环还没有执行完 length-1 次也可以直接 break。
function bubbleSort1(arr) {
for (let i = 0; i < arr.length - 1; i++) {
// 外层循环初始值为 false,没有发生交换
let has_exchanged = false
for (let j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j ,j+1)
has_exchanged = true
}
}
// 内层循环结束判断一下是否发生了交换
if (!has_exchanged) break
}
return arr
}
优化2
记录内层遍历最后一次发生交换的位置,下一次外层遍历只需要到这个位置就可以了。
那么外层遍历就不能用 for 了,因为每次遍历的结束位置可能会发生改变。
function bubbleSort2(arr) {
// 遍历结束位置的初始值为数组尾,并逐渐向数组头部逼近
let high = arr.length - 1
while (high > 0) {
// 本次内层遍历发生交换的位置的初始值
let position = 0
for (let j = 0; j < high; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1)
// 如果发生了交换,更新 position
position = j
}
}
// 下次遍历只需要到 position 的位置即可
high = position
}
return arr
}
优化3
双向遍历,每次循环能找到一个最大值和一个最小值。
前后各设置一个索引,向中间的未排序部分逼近。
function bubbleSort3(arr) {
let low = 0, high = arr.length - 1
while (low < high) {
// 正向遍历找最大
for (let i = low; i <= high; i++) if (arr[i] > arr[i + 1]) swap(arr, i, i + 1)
high--
// 反向遍历找最小
for (let j = high; j >= low; j--) if (arr[j] < arr[j - 1]) swap(arr, j, j - 1)
low++
}
return arr
}
选择排序 Selection Sort
每次遍历选择最小。
排序后的元素将放在数组前部
大致流程:
- 取出未排序部分的第一个元素,遍历该元素之后的部分并比较大小。对于第一次遍历,就是取出第一个元素
- 如果有更小的,与该元素交换位置
- 每次遍历都能找出剩余元素中的最小值并放在已排序部分的最后
并不是倒着的冒泡排序。冒泡排序是比较相邻的两个元素
演示图:
function selectionSort(arr) {
for (let i = 0; i < arr.length; i++) {
let min_index = i
// 遍历后面的部分,寻找更小值
for (let j = i + 1; j < arr.length; j++) {
// 如果有,更新min_index
if (arr[j] < arr[min_index]) min_index = j
}
swap(arr, i, min_index)
}
return arr
}
堆排序 HeapSort
使用堆的概念实现的选择排序。
首先,关于堆:
- 堆是树的一种。当堆的父节点都大于,或者都小于子节点时,分别称为最大堆或最小堆
- 可以用数组来表示树(堆)。从0开始,以数组的第
index个元素为堆的父节点,其左右子节点分别为数组的第2*index+1和2*index+2个元素
已排序元素将放在数组尾部
大致流程:
- 建最大堆:把数组整理为最大堆的顺序,那么堆的根节点,或者说数组的第一个元素,就是最大的值
- 排序:把最大值与未排序部分的最后一个元素交换,剩余的部分继续调整为最大堆。每次建堆都能找到剩余元素中最大的一个
注意:
- 第一次建堆时,只需要遍历数组左侧一半元素就够了,并且要从中点向左侧倒序遍历,这样才能保证把最大的元素移动到数组头部
- 排序时,当然就需要遍历数组里所有元素了
演示图:

// 排序
function heapSort(arr) {
var arr_length = arr.length
if (arr_length <= 1) return arr
// 1. 建最大堆
// 遍历一半元素就够了
// 必须从中点开始向左遍历,这样才能保证把最大的元素移动到根节点
for (var middle = Math.floor(arr_length / 2); middle >= 0; middle--) maxHeapify(arr, middle, arr_length)
// 2. 排序,遍历所有元素
for (var j = arr_length; j >= 1; j--) {
// 2.1. 把最大的根元素与最后一个元素交换
swap(arr, 0, j - 1)
// 2.2. 剩余的元素继续建最大堆
maxHeapify(arr, 0, j - 2)
}
return arr
}
// 建最大堆
function maxHeapify(arr, middle_index, length) {
// 1. 假设父节点位置的值最大
var largest_index = middle_index
// 2. 计算左右节点位置
var left_index = 2 * middle_index + 1,
right_index = 2 * middle_index + 2
// 3. 判断父节点是否最大
// 如果没有超出数组长度,并且子节点比父节点大,那么修改最大节点的索引
// 左边更大
if (left_index <= length && arr[left_index] > arr[largest_index]) largest_index = left_index
// 右边更大
if (right_index <= length && arr[right_index] > arr[largest_index]) largest_index = right_index
// 4. 如果 largest_index 发生了更新,那么交换父子位置,递归计算
if (largest_index !== middle_index) {
swap(arr, middle_index, largest_index)
// 因为这时一个较大的元素提到了前面,一个较小的元素移到了后面
// 小元素的新位置之后可能还有比它更大的,需要递归
maxHeapify(arr, largest_index, length)
}
}
插入排序 Insertion Sort
一般实现
已排序元素将放在数组前部
大致流程:
- 取未排序部分的第一个元素。第一次遍历时,将第一个元素作为已排序元素,从第二个元素开始取
- 遍历前面的已排序元素,并与这个未排序元素比较大小,找到合适的位置插入
- 继续执行1
第一种理解方式,也就是一般的实现原理:
在上面的第2步中,遍历已排序元素时,如果该未排序元素仍然小于当前比较的已排序元素,就把前一个已排序元素的值赋给后一个位置上的元素,也就是产生了两个相邻的重复元素。
这样一来,在比较到最后,找到合适的位置时,用该未排序元素给两个重复元素中合适的那一个赋值,覆盖掉一个,排序就完成了。
叙述可能不够清楚,看后面的代码就是了。
Talk is hard, show you some codes。
和选择排序好像有一点类似的地方:
- 选择排序,先找合适的元素,然后直接放到已排序部分
- 插入排序,先按顺序取元素,再去已排序部分里找合适的位置
第二种理解方式:
在前面的第2步中,相当于把已排序部分末尾添加一个元素,并且执行一次冒泡排序。 因为前面的数组是已排序的,所以冒泡只需要遍历一次就可以给新的元素找到正确的位置。
但是以这种方式实现的代码无法使用二分法进行优化。
那么是不是说明,冒泡排序的优化方法可以用在这里?
并不是。因为冒泡排序主要从两方面进行优化:
- 减少外层遍历次数
- 增加每次遍历找到的极值个数
而这里的冒泡只有一次,并且也不是找极值。
演示图:
// 按照第一种理解方式的实现,即一般的实现
function insertionSort(arr) {
for (let index = 1; index < arr.length; index++) {
// 取出一个未排序元素
let current_ele = arr[index]
// 已排序元素的最后一个的位置
let ordered_index = index - 1
// 前面的元素更大,并且还没遍历完
while (arr[ordered_index] >= current_ele && ordered_index >= 0) {
// 使用前面的值覆盖当前的值
arr[ordered_index + 1] = arr[ordered_index]
// 向前移动一个位置
ordered_index--
}
// 遍历完成,前面的元素都比当前元素小,把未排序元素赋值进去
arr[ordered_index + 1] = current_ele
}
return arr
}
// 按照第二种理解方式的实现
function insertionSort(arr) {
for (let i = 0; i < arr.length; i++) {
// 对前面的已排序数组和新选出来的元素执行一趟冒泡排序
for (let j = i + 1; j >= 0; j--) if (arr[j] < arr[j - 1]) swap(arr, j, j - 1)
}
return arr
}
一个意外的弱智发现:while(a&&b){} 和 while(a){ if(b){} } 不等价。。。
优化
使用二分查找。
遍历已排序部分时,不再是按顺序挨个比较,而是比较中位数。
function binaryInsertionSort(array) {
for (let i = 1; i < array.length; i++) {
// 未排序部分的第1个
let current_ele = array[i]
// 已排序部分的第1个和最后1个
let left = 0, right = i - 1
// 先找位置
while (left <= right) {
// 不再是从最后一个位置开始向前每个都比较,而是比较中间的元素
let middle = parseInt((left + right) / 2)
if (current_ele < array[middle]) right = middle - 1
else left = middle + 1
}
// while结束,已经找到了一个大于或等于当前元素的位置 left
// 再修改数组:把 left 到 i 之间的元素向后移动一个位置
for (let j = i - 1; j >= left; j--) array[j + 1] = array[j]
// 插入当前元素
array[left] = current_ele
}
return array
}
插入排序使用的二分查找和二分查找函数显然不同。
因为两者的目的不相同。
二分查找函数需要返回“存在”或“不存在”;而插入排序中的二分查找,关注的不是存在与否,而是“位置应该在哪里”,不管存在不存在,都要返回一个位置。
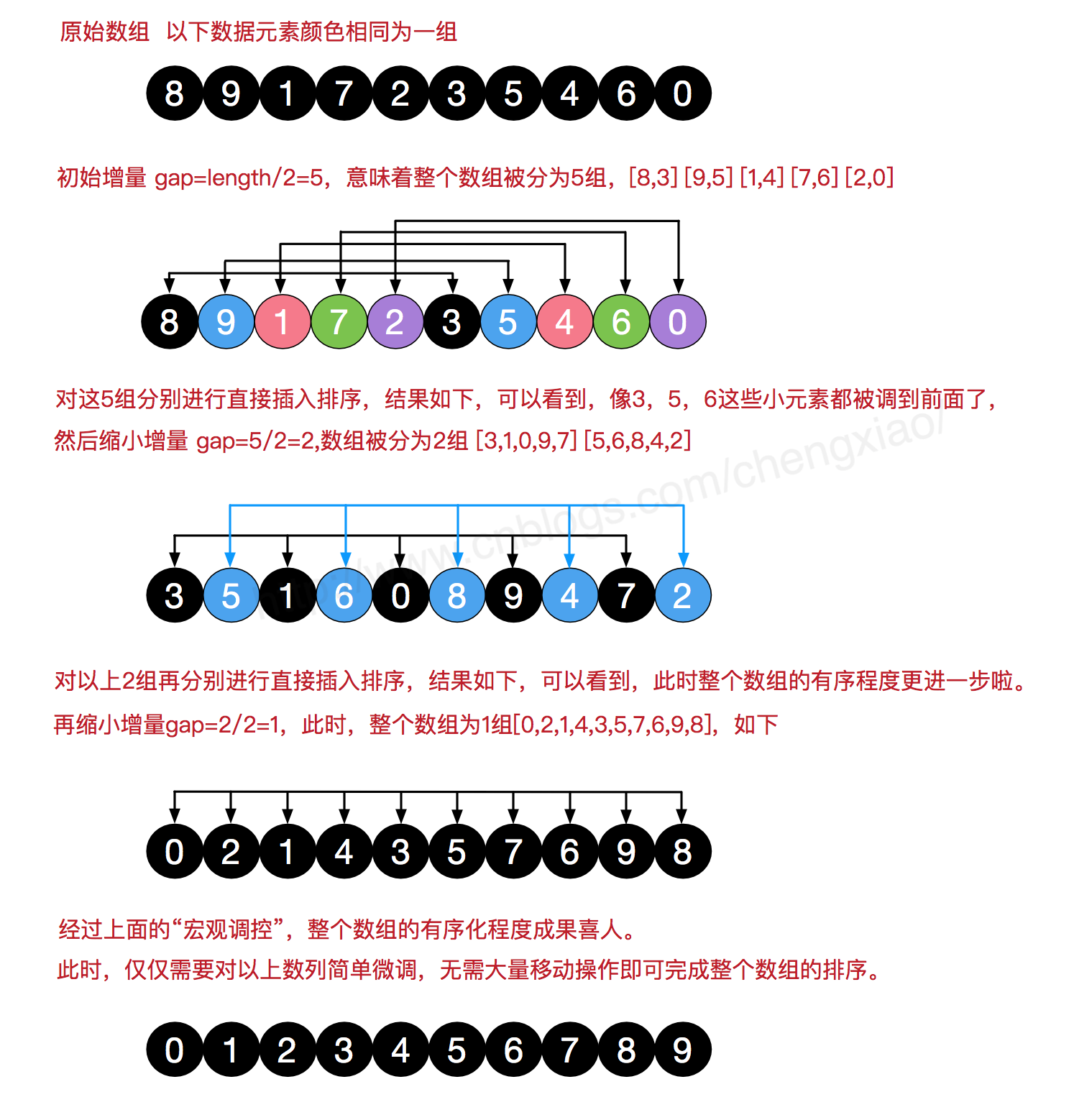
希尔排序 Shell Sort
也叫缩小增量排序,是插入排序的增强版。
不直接对整个数组执行插入排序,而是先分组,对每个组的元素执行插入排序,使数组大致有序,逐步提高这个“大致”的精确度,也就是减少分组的数量,直到最后只有一组。
指定一个增量 gap,对数组分组,使得每相距 gap-1 的元素为一组,共分成 gap 组,对每组执行插入排序。逐步缩小 gap 的大小并继续执行插入排序,直到为1,也就是整个数组作为一组,对整个数组执行插入排序。
可以发现,不管增量 gap 初始值设定为多少,最后总会对整个数组进行一次插入排序,也就是说 gap 对排序结果是没有影响的,只是影响了算法效率。
至于 gap 如何取值最好,还没有研究过。期待大家留言交流。(只是随便一说,我看这个单纯就是为了面试。。)
大致流程:
- 共三层循环,外层循环用来逐步减少
gap的值 - 中层与内层两层循环基本上就是插入排序,细节上的不同直接看代码就好,不再赘述
演示图:
function shellSort(arr) {
// 外层循环逐步缩小增量 gap 的值
for (let gap = 5; gap > 0; gap = Math.floor(gap / 2)) {
// 中层和内层是插入排序
// 普通插入排序从第1个元素开始,这里分组了,要看每一组的第1个元素
// 共分成了 gap 组,第一组的第1个元素索引为 gap
// 第一组元素索引为 0, 0+gap, 0+2*gap,...,第二组元素索引为 1, 1+gap, 2+2*gap,...
for (let i = gap; i < arr.length; i++) {
let current_ele = arr[i]
// 普通插入排序时,j 每次减少1,即与前面的每个元素比较
// 这里 j 每次减少 gap,只会与当前元素相隔 n*(gap-1) 的元素比较,也就是只会与同组的元素比较
let ordered_index = i - gap
while (ordered_index >= 0 && arr[ordered_index] > current_ele) {
arr[ordered_index + gap] = arr[ordered_index]
ordered_index -= gap
}
arr[ordered_index + gap] = current_ele
}
}
return arr
}
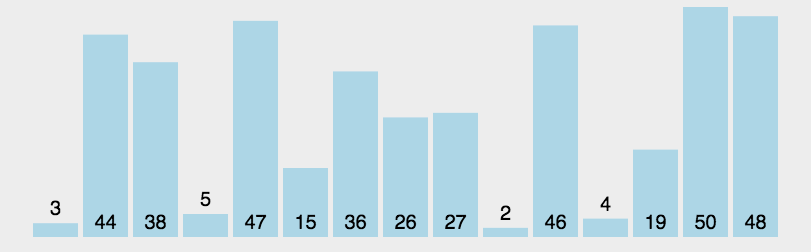
快速排序 Quick Sort
大致流程:
- 选择一个基准元素
pivot,比如第一个元素当然可以选其他元素,但是最后会递归至只剩一个元素,所以还是选第一个元素比较靠谱
- 遍历数组,比
pivot更小的元素创建一个数组,更大的创建一个数组,相等的也创建一个数组 - 递归大小两个数组,继续执行1,直到数组只剩1个元素;递归的同时把这三部分连接起来
普通快速排序没有考虑与
pivot相等的情况,只建了更小和更大的两个数组。
像上面考虑与pivot相等的情况时,又叫做三路快排。
演示图:
function quickSort(arr) {
// 只剩1个元素,不能再分割了
if (arr.length <= 1) return arr
// 取第1个元素为基准值
let base = arr[0]
// 分割为左小右大两个数组,以及包含元素本身的中间数组
let left = [], middle = [base], right = []
for (let index = 1; index < arr.length; index++) {
// 如果有与本身一样大的元素,放入 middle 数组,解决重复元素的问题
if (arr[index] === base) middle.push(arr[index])
else if (arr[index] < base) left.push(arr[index])
else right.push(arr[index])
}
// 递归并连接
return quickSort(left).concat(middle, quickSort(right))
}
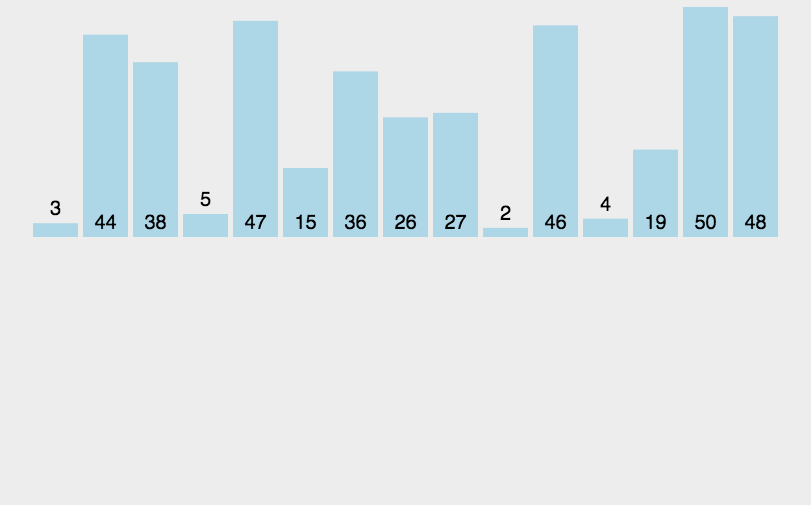
归并排序 Merge Sort
是采用分治法(Divide and Conquer)的一个非常典型的应用。
简单说就是缩小问题规模,快速排序也是分治法
大致流程:
-
递归地把数组分割成前后两个子数组,直到数组中只有1个元素
直接分两半,不用排序
-
同时,递归地从两个数组中挨个取元素,比较大小并合并
演示图:
// 分割
function mergeSort2(arr) {
// 如果只剩一个元素,分割结束
if (arr.length < 2) return arr
// 否则继续分成两部分
let middle_index = Math.floor(arr.length / 2),
left = arr.slice(0, middle_index),
right = arr.slice(middle_index)
return merge2(mergeSort2(left), mergeSort2(right))
}
// 合并
function merge2(left, right) {
let result = []
// 当左右两个数组都还没有取完的时候,比较大小然后合并
while (left.length && right.length) {
if (left[0] < right[0]) result.push(left.shift())
else result.push(right.shift())
}
// 其中一个数组空了,另一个还剩下一些元素
// 因为是已经排序过的,所以直接concat就好了
// 注意 concat 不改变原数组
if (left.length) result = result.concat(left)
if (right.length) result = result.concat(right)
return result
}
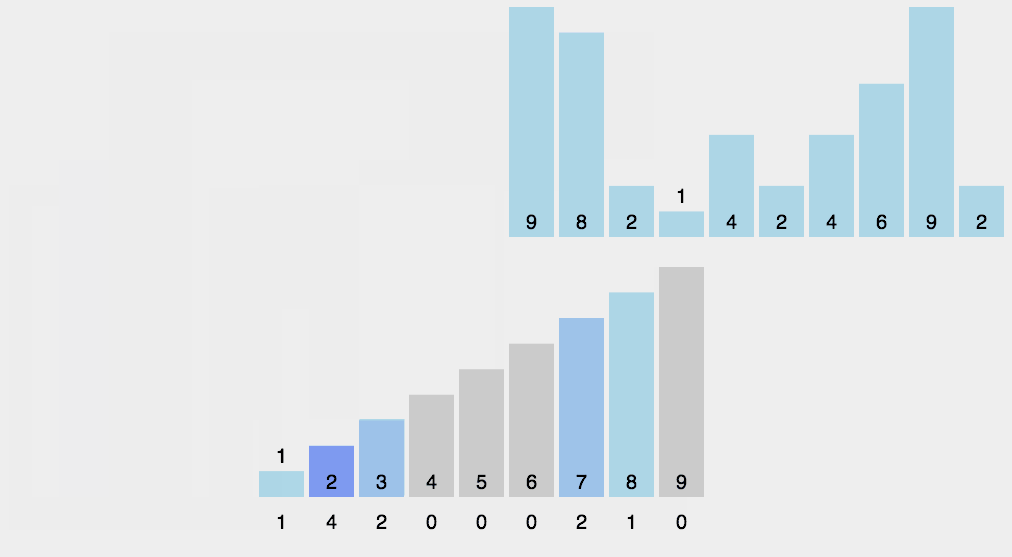
计数排序 Counting Sort
只能用于由确定范围的整数所构成的数组。
统计每个元素出现的次数,新建一个数组 arr,新数组的索引为原数组元素的值,每个位置上的值为原数组元素出现的次数。
大致流程:
- 遍历数组,找出每个元素出现的次数,放入统计数组
- 遍历统计数组,放入结果数组
演示图:
function countingSort(array) {
let count_arr = [], result_arr = []
// 统计出现次数
for (let i = 0; i < array.length; i++) {
count_arr[array[i]] = count_arr[array[i]] ? count_arr[array[i]] + 1 : 1
}
// 遍历统计数组,放入结果数组
for (let i = 0; i < count_arr.length; i++) {
while (count_arr[i] > 0) {
result_arr.push(i)
count_arr[i]--
}
}
return result_arr
}
桶排序 Bucket Sort
根据原数组的最小和最大值的范围,划分出几个区间,每个区间用数组来表示,也就是这里所说的桶。
根据元素大小分别放入对应的桶当中,每个桶中使用任意算法进行排序,最后再把几个桶合并起来。
区间的数量一般是手动指定的。
基本流程:
- 初始化指定个数的桶
- 找到数组的最大值和最小值,作差并除以桶数,就得到了每个桶中值的范围
range - 遍历数组,每个元素的值除以
range,商的整数部分即对应的桶的索引,放入该桶 - 入桶时,可以立即执行排序,而不只是单单的
push(),比如使用插入排序 - 遍历结束时,每个桶中的元素都是排序好的。并且因为桶也是按顺序摆放的,直接把所有的桶按顺序
concat起来即可
其他排序方法当然也可以。不过插入排序实现时更接近“给已排序数组新增一个元素并使之有序”这种目的。
演示图:
function bucketSort(array, num) {
let buckets = [],
min = Math.min(...array),
max = Math.max(...array)
// 初始化 num 个桶
for (let i = 0; i < num; i++) buckets[i] = []
// (最大值-最小值)/桶数,得到每个桶最小最大值的差,即区间
// 比如 range 为10, 0号桶区间为0-10,1号桶10-20,...
let range = (max - min + 1) / num
for (let i = 0; i < array.length; i++) {
// (元素-最小值)/区间,取整数部分,就是应该放入的桶的索引
let bucket_index = Math.floor((array[i] - min) / range),
bucket = buckets[bucket_index]
// 空桶直接放入
if (bucket.length) {
bucket.push(array[i])
}
// 非空,插入排序
else {
let i = bucket.length - 1
while (i >= 0 && bucket[i] > array[i]) {
bucket[i + 1] = bucket[i]
i--
}
bucket[i + 1] = array[i]
}
}
// 合并所有桶
let result = []
buckets.forEach((bucket) => {
result = result.concat(bucket)
})
return result
}
一个题外话,关于 Array 的 fill() 方法。
在初始化数组的时候,想着是不是可以用 let arr = new Array(4).fill([]),一行代码就可以给数组添加初始元素,这样就不用先创建数组,然后再 for 循环添加元素了。
但是问题是,fill() 添加的引用类型元素——这里就是空数组 []——它们指向的是同一个引用。如果修改了其中一个数组,其他的数组也都跟着变了。
还是老老实实 for 循环吧。
基数排序 Radix Sort
要求元素必须是0或正整数。
通过比较每个元素对应位置上数字的大小进行排序:个位与个位,十位与十位 ...
根据比较顺序不同,分为两类:
- Least Significant Digit,从个位开始比较
- Most Significant Digit,从最高位开始比较
两种方法的共同点是:
- 先要找到最大的元素。因为每个元素的每一位都要对应比较,所以要看最大的元素有几位
- 当其中一个元素某一位上没有值时,以0代替
LSD
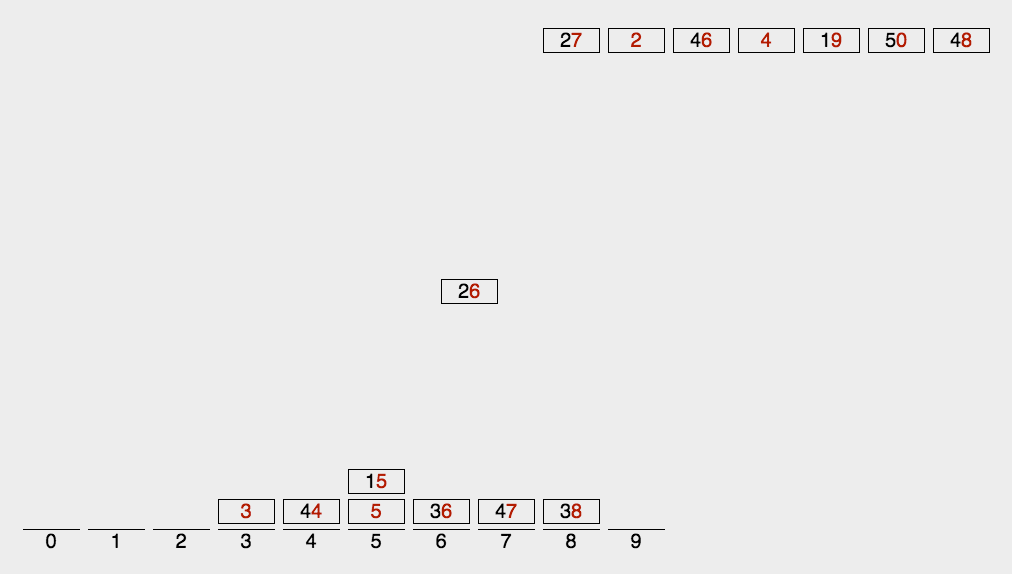
插播一曲 LSD: Lucy in the Sky with Diamonds
基本流程:
先看一下演示图比较好
- 找出最大元素,并获取其位数(长度)
max_len - 外层循环以
max_len作为遍历次数,从个位开始;内层循环遍历数组 - 每次外层循环,都比较元素该位上的数字
- 每次外层循环的最开始,先初始化 10 个数组,或者叫做桶,表示该位上的数字是 0-9 其中的一个
- 内层遍历根据每个元素当前位上的值放到对应的桶里
- 每次外层循环结束,把 10 个桶里的元素按顺序取出,并覆盖原数组,得到一个排序过后的数组
演示图:
function radixSortLSD(arr) {
// 找出最大元素
let max_num = Math.max(...arr),
// 获取其位数
max_len = getLengthOfNum(max_num)
console.log(`最大元素是 ${max_num},长度 ${max_len}`)
// 外层遍历位数,内层遍历数组
// 外层循环以最大元素的位数作为遍历次数
for (let digit = 1; digit <= max_len; digit++) {
// 初始化0-9 10个数组,这里暂且叫做桶
let buckets = []
for (let i = 0; i < 10; i++) buckets[i] = []
// 遍历数组
for (let i = 0; i < arr.length; i++) {
// 取出一个元素
let ele = arr[i]
// 获取当前元素该位上的值
let value_of_this_digit = getSpecifiedValue(ele, digit)
// 根据该值,决定当前元素要放到哪个桶里
buckets[value_of_this_digit].push(ele)
console.log(buckets)
}
// 每次内层遍历结束,把所有桶里的元素依次取出来,覆盖原数组
let result = []
buckets.toString().split(',').forEach((val) => {
if (val) result.push(parseInt(val))
})
// 得到了一个排过序的新数组,继续下一轮外层循环,比较下一位
arr = result
console.log(arr)
}
}
function getLengthOfNum(num) { return (num += '').length }
// 获取一个数字指定位数上的值,超长时返回0
// 个位的位数是1,十位的位数是2 ...
function getSpecifiedValue(num, position) { return (num += '').split('').reverse().join('')[position - 1] || 0 }
MSD
这个没图,不过更简单,也不需要图。
现实生活中比较数字大小的时候一般也是这么做的,先比较最高位,然后再看更小位。
基本流程:
- 找出最大元素,获取位数
- 从最高位开始,比较每个元素相同位置上的数字,分桶
- 如果还没比较到个位,那么递归每个不为空的桶,继续比较他们的下一位
举两个栗子。
没有重复元素的情况:
// 原始数组
[110, 24, 27, 56, 9]
// 原数组相当于
[110, 024, 027, 056, 009]
// 第一次入桶,比较最高位百位
[[024, 027, 056, 009], [110]]
// 当桶中有多个元素时,递归。这里就是递归第一个桶
// 第二次入桶,比较十位
[[[009], [024, 027], [056]], [110]]
// 第二个桶中还有元素,继续递归
// 第三次入桶,比较个位
[[[009], [[024], [027]], [056]], [110]]
// 结果就是
[009, 024, 027, 056, 110]
也就是说,对于没有重复元素的情况,递归的最终结果是每个桶中只有一个元素。
有重复元素的情况:
[110, 024, 024, 056, 009]
// 第一次入桶,比较百位
[[009, 024, 024, 056], [110]]
// 第二次入桶,比较十位
[[[009], [024, 024], [056]], [110]]
// 第三次入桶,比较个位
[[[009], [[024, 024]], [056]], [110]]
可以发现,对于有重复元素的情况,最终重复的元素都会在同一个桶中,不会产生每个桶中只有一个元素的结果。
这时只要判断是否已经比较完个位了即可。也就是说,不管有没有重复元素,最大元素有几位,就最多需要比较多少次。
总之,可以想象成一个树结构,从原数组开始一直向下分出子数组,最后子数组中只有一个元素,或只有重复的元素。
function radixSortMSD(arr) {
// 最大元素
let max_num = Math.max(...arr),
// 获取其位数作为初始值,最小值为1,也就是个位
digit = getLengthOfNum(max_num)
return msd(arr, digit)
}
function msd(arr, digit) {
// 建10个桶
let buckets = []
for (let i = 0; i < 10; i++) buckets[i] = []
// 遍历数组,入桶。这里跟 LSD 一样
for (let i = 0; i < arr.length; i++) {
let ele = arr[i]
let value_of_this_digit = getSpecifiedValue(ele, digit)
buckets[value_of_this_digit].push(ele)
}
// 结果数组
let result = []
// 遍历每个桶
for (let i = 0; i < buckets.length; i++) {
// 只剩一个元素,直接加入结果数组
if (buckets[i].length === 1) result = result.concat(buckets[i])
// 还有多个元素,但是已经比较到个位了
// 说明是重复元素的情况,也直接加入结果数组
else if (buckets[i].length && digit === 1) result = result.concat(buckets[i])
// 还有多个元素,并且还没有比较结束,递归比较下一位
else if (buckets[i].length && digit !== 1) result = result.concat(msd(buckets[i], digit - 1))
// 空桶就不作处理了
}
return result
}
参考链接
十大经典排序算法总结(JavaScript描述) - 掘金
前端 排序算法总结 - segmentfault
JS快速排序&三路快排
图解排序算法(二)之希尔排序
计数排序,桶排序与基数排序 - segmentfault
时间复杂度 - 维基
比较排序 - 维基
打个广告
我的其他文章:
《深入 JavaScript 常用的8种继承方案》
《免费为网站添加 SSL 证书》
《详解 new/bind/apply/call 的模拟实现》