零、前言
最大子序列和问题
这个问题是《数据结构和算法分析》一书中的一个问题,书中给了四种算法
我感觉它是入手算法很不错的一个问题,本文算法源于书中,但文中包含了我的分析和理解

2.题目的分析
也许很多人看到题目就懵圈了,这里解释一下:
拿一个例子来说: -2,11,-4,13,-5,-2
它的子序列是什么意思: 连续的若干个元素, 比如:11,-4和-4,13,-5,-2等
该问题也就是说:这些子序列元素的和最大是多少,以下列出了所有子序列的情况及子序列和

一、第一种算法
1.具体算法
根据上面分析的图,很容易可以想到第一种算法:
private static int maxSonNum(int[] a) {
int maxSum = 0;
for (int i = 0; i < a.length; i++) {
for (int j = i; j < a.length; j++) {
int sum = 0;
for (int k = i; k <= j; k++) {
sum += a[k];
}
if (sum > maxSum) {
maxSum = sum;
}
}
}
return maxSum;
}
2.算法分析
可以说下面是我发明的for循环的简单图示:简称
for图
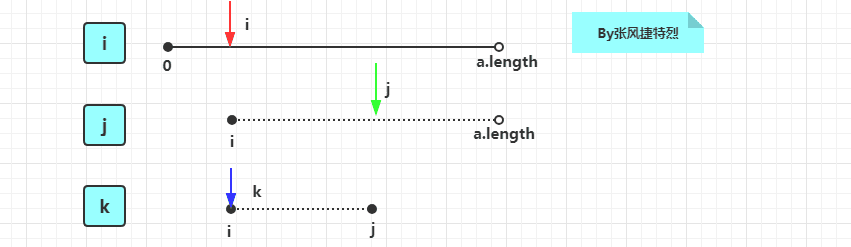
[1].一条线代表一个for循环
[2].线的左边是for循环中索引的变量名
[3].线两端数字表示循环的范围,空心代表不包含,实心表示包含
[4].箭头表示某个时刻的遍历情况
[5].内部循环在下边,可以看成底部箭头向右走,走到头上面的箭头右动一格(类似时钟,分针,秒针)
想像一下,看脑中是否可以出现for循环中运动的场景:
k 箭头向右走,计算`i~j`子序列的和,并维护maxSum的值。当走到 j 时,发出"刺啦"一声
j 箭头向右移一格,发出一声"嗒"。然后k箭头再跑,直到j跑到a.length之后
i 箭头右移一格, 发出一声"叮",j 箭头在k箭头的推动下一点点跑,直到i跑到了a.length
交响乐大概就是这样的吧:
...
刺啦,嗒,刺啦,嗒,刺啦,嗒,叮
刺啦,嗒,刺啦,嗒,刺啦,嗒,刺啦,嗒,叮
刺啦,嗒,刺啦,嗒,刺啦,嗒,刺啦,嗒,刺啦,嗒,叮
...
从上面来看,这个算法虽然可以解决问题,使用了三层,每层都是N的复杂度
时间复杂度为O(N^3),可想而知,非常耗时
二、第二种算法
1.具体算法
private static int maxSonNum(int[] a) {
int maxSum = 0;
for (int i = 0; i < a.length; i++) {
int sum = 0;
for (int j = i; j < a.length; j++) {
sum += a[j];
if (sum > maxSum) {
maxSum = sum;
}
}
}
return maxSum;
}
2.算法分析
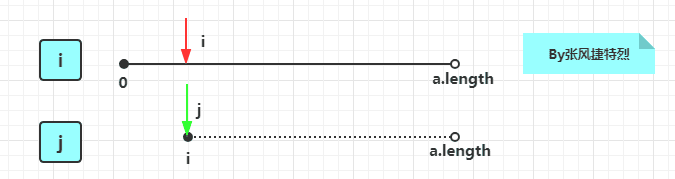
刚才:在j的循环中新开了一个k循环计算i~j的元素和
如 i=0,j=4 时:子序列 -2,11,-4,13,-5 用一个k循环就算他们的和
这里:在j的循环中维护sum变量也能达到一样的效果:
如 i=0,j=4 时:sum= sum + -5 即 -2+11-4+13-5,然后维护maxSum
这样就减少一层for循环:时间复杂度为O(N^2)
三、第三种算法
1.具体算法
分治的思想,也是本文最想讲的内容
private static int maxSumRec(int[] a, int start, int end) {
if (start == end) {
return a[start];//一个元素的最大子序列是其本身
}
int center = (start + end) / 2;
int maxLeftSum = maxSumRec(a, start, center);//1.左半最大子序列和
int maxRightSum = maxSumRec(a, center + 1, end);//2.右半最大子序列和
/*
3.如果最大子序列和贯穿左右时:
|--- 1.子序列是连续的
|--- 2.中点和中点的后面元素在最大子序列中
*/
//寻找左半中含左半一个元素的最大子序列和
int maxLeftSBorderSum = 0, leftBorderSum = 0;
for (int i = center; i >= start; i--) {
leftBorderSum += a[i];
if (leftBorderSum > maxLeftSBorderSum) {
maxLeftSBorderSum = leftBorderSum;
}
}
//判断右半中含右半第一个元素的最大子序列和
int maxRightSBorderSum = 0, rightBorderSum = 0;
for (int i = center + 1; i <= end; i++) {
rightBorderSum += a[i];
if (rightBorderSum > maxRightSBorderSum) {
maxRightSBorderSum = rightBorderSum;
}
}
return max3(maxLeftSum, maxRightSum, maxLeftSBorderSum + maxRightSBorderSum);
}
private static int max3(int a, int b, int c) {
int max;
if (a > b && a > c) {
max = a;
} else if (c > a && c > b) {
max = c;
} else {
max = b;
}
return max;
}
2.算法分析
将一个大问题拆解成若干个小问题,使用递归来解决 虽然算法复杂了很多,但运行的时间复杂度降到了O(NlongN),还是很有价值的
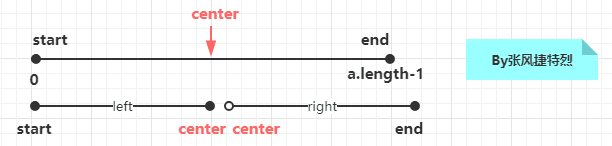
最大子序列和可能存在于:
1.左半的序列:maxLeftSum
2.由半的序列:maxRightSum
3.该序列贯穿左右
|--- 判断左半(子序列含:左半最后一个元素):maxLeftSBorderSum
|--- 判断右半(子序列含:右半第一个元素):maxRightSBorderSum
寻找子序列即(含左半最后一个元素),又含(右半第一个元素),说明两半序列可连续
int maxLeftSBorderSum = 0, leftBorderSum = 0;
for (int i = center; i >= start; i--) {//遍历包含center点的最侧子序列取最大和
leftBorderSum += a[i];
if (leftBorderSum > maxLeftSBorderSum) {
maxLeftSBorderSum = leftBorderSum;
}
}
int maxRightSBorderSum = 0, rightBorderSum = 0;
for (int i = center + 1; i <= end; i++) {//遍历包含center+1点的右侧子序列取最大和
rightBorderSum += a[i];
if (rightBorderSum > maxRightSBorderSum) {
maxRightSBorderSum = rightBorderSum;
}
}
maxLeftSBorderSum和maxRightSBorderSum由于包含center点和center+1点
所以是贯穿左右的子序列,并且其和是[贯穿左右的子序列]中最大的
具体来分析一下问题的分解
Q1: 求 -2 11 -4 13 -5 -2 的最大子序列和
Q1可以分解为下面三个问题的最大值:
|---Q1.1: -2 11 -4 的最大子序列和
|---Q1.2: 13 -5 -2 的最大子序列和
|---Q1.3: 序列和最大值贯穿左右时的最大值:
|--- 判断左半:序列含左半最后一个元素的子序列最大值
|--- 判断右半:序列含右半第一个元素子序列最大值
Q1.1可以分解为下面三个问题的最大值:
|---Q1.1.1: -2 11 的最大子序列和
|---Q1.1.2: -4 的最大子序列和 -4
|---Q1.1.3: 序列和最大值贯穿左右时的最大值:
|--- 判断左半:序列含左半最后一个元素的子序列最大值 11
|--- 判断右半:序列含右半第一个元素子序列最大值 -4
Q1.1.1可以分解为下面三个问题的最大值:
|---Q1.1.1.1: -2 的最大子序列和 -2
|---Q1.1.1.2: 11 的最大子序列和 11
|---Q1.1.1.3: 序列和最大值贯穿左右时的最大值:
|--- 判断左半:序列含左半最后一个元素的子序列最大值 -2
|--- 判断右半:序列含右半第一个元素子序列最大值 11
所以 Q1.1.1 = 11 Q1.1.2 = -4 Q1.1.3 = 7
所以 Q1.1 = 11 同理分解 Q1.2 = 13 Q1.3 = 7 + 13 =20
所以 Q1 = 20 得解
四、 第四种算法
1.具体算法
private static int maxSonNum4(int[] a) {
int maxSum = 0, sum = 0;
for (int i = 0; i < a.length; i++) {
sum += a[i];
if (sum > maxSum) {
maxSum = sum;
} else if (sum < 0) {
sum = 0;
}
}
return maxSum;
}
2.分析
反正我是很难想像第一个写出这个算法的人脑子是怎么想的,也很难去说明这个算法的正确性
这在O(N)的时间完成了最大子序列和问题,这种"简洁和聪明以及高效"也许就是算法的迷人之处。
-2 11 -4 13 -5 -2
sum maxSum sum
i = 0 -2 0 0
i = 1 11 11 11
i = 2 7 11 7
i = 3 20 20 20
i = 4 15 20 15
i = 5 13 20 13
一种算法可以从O(N^3)优化到O(N^2),再用分治优化到O(NlogN)
最后被一个O(N)的算法亮瞎的的钛合金言,所以这个问题真的挺有意思。