背景
二叉树算是难度相对较高的一种数据结构
它的种类很多,衍生出来的题目类型也千变万化
想要面面俱到仅仅通过一篇博客很难做到,而且效果也不会很好
由于它的基本结构以及二叉树类型题目的解决思路大致相同
所以这里我们有针对性的挑两道题目进行讲解,如果有问题大家也可以在评论区进行讨论
对称二叉树
LeetCode第101题 原题地址
题目难度: 简单
题目描述
给定一个二叉树,检查它是否是镜像对称的。 例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
示例1:二叉树[1,2,2,3,4,4,3]是对称的,返回true
1 / \ 2 2 / \ / \ 3 4 4 3
示例2:二叉树[1,2,2,null,3,null,3]则不是镜像对称的,返回false
1 / \ 2 2 \ \ 3 3
要求: 传入root(根节点),返回true或false
题目理解
- 理解数据结构
由于这道题直接传入了已实现好的二叉树,而有的同学可能不清楚这种数据结构具体是怎样的
所以在分享解题思路之前我们先来介绍一下二叉树的数据结构(觉得啰嗦的同学可以跳过这一节)
题目中使用了数组的格式来表示二叉树的结构
(使用数组表示只是为了方便理解 并不代表二叉树是一个数组)
将二叉树的所有节点逐行从左至右排列到数组中,为每个节点的左右子节点都保留位置,如果没有则表示为null。
如[1,2,2,3,4,4,3]对应
1
/ \
2 2
/ \ / \
3 4 4 3
[1,2,2,null,3,null,3]对应
1
/ \
2 2
\ \
3 3二叉树中每一个节点可以看作是一个对象,他包含三部分:
- 节点的值val
- 指向左节点的指针left(若没有左结点默认为null)
- 指向右节点的指针right(若没有右结点默认为null)
拿示例1进行举例
1
/ \
2 2
/ \ / \
3 4 4 3我们将根节点命名为root,则节点间的对应关系为:
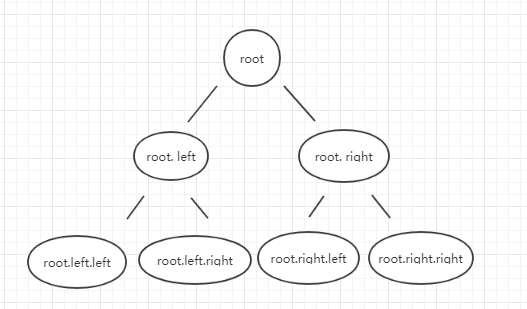
则结合示例中给出的值我们可以得出:
- root.val = 1
- root.left.val = 2
- root.right.val = 2
- ...
结构我们理清了,接下来分析一下题目要求
- 分析题目要求
题目中要求传入的是一个根节点root
我们通过根节点以及它后代的left和right指针可以还原整个二叉树
最后根据还原出的二叉树判断其是否对称。
这道题目不是很复杂,我们可以给还原出来的二叉树画一条中垂线,我们想象沿着这条线对折
若两侧的节点可以完全重合并且对应节点的值相同那么它就是对称的。
如示例1:
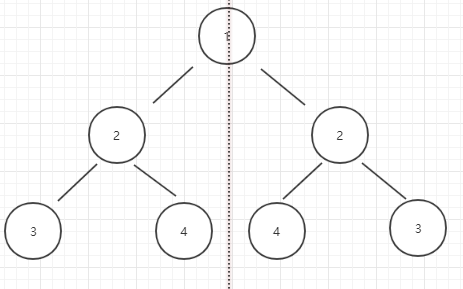
很明显,它是符合要求的。
思路分析
我们可以注意到:
除了根节点以外的任意一个节点A,只要找到它关于轴的对称点A1,若二者val值相等,就代表这两个节点满足'对称'条件,如果找到了该二叉树中所有的对称点并且都符合条件,我们就可以断定这个二叉树是'对称'的。
我在上篇博客《JS版数据结构第四篇(矩阵)》中有总结过我们使用递归方法的三个通用条件:
- 可以将一个操作拆解为处理过程相同的小步骤
- 每次步骤的输入数据格式都相同
- 运行次数未知
大家思考一下这道题目是不是依然符合递归的三个条件:
- 首先我们将 检查二叉树是否对称 转换成 每两个对称点的比较
- 每次传入两个对称的节点
- 递归直到二叉树中所有节点比较完毕
那我们怎么保证每次传入的都是对称的两个点呢?
其实只要每次递归时传入当前两个节点的子节点的对称点即可
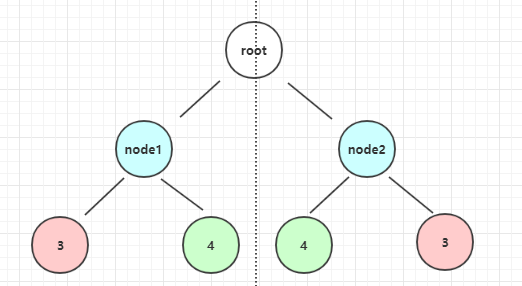
如在这个图中
我们最开始比较的是node1和node2,
我们比较完这两个节点后要继续递归他们子节点对称点的比较
所以接下来我们需要比较的就是
node1.left和node2.right
node1.right和node2.left
如果有后代的话会继续传入他们后代的对称点
如果你不是很清楚也没有关系,接下来我们用代码实现一下。
代码实现
// root 是根节点 二叉树结构已实现
root => {
// 如果根节点为空 返回true
if(!root) {
return true
}
// map函数用来比较两个节点是否完全相同
// @param1{Object}节点1
// @param2{Object}节点1的对称点
let map = (node1,node2) => {
// 两个节点都不存在 返回true
if(!node1 && !node2){
return true
}
// 其中一个节点不存在或两个节点值不相等,返回false
if(!node1 || !node2 || node1.val !== node2.val){
return false
}
// 遍历当前两个对称点的子节点的对称点
return map(node1.left, node2.right) && map(node2.right, node2.left)
}
// 初始传入根节点的左右节点
return map(root.left, root.right)
}验证二叉搜索树
LeetCode第98题 原题地址
题目难度: 中等
题目描述
示例1:给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
输入:
2
/ \
1 3
输出: true示例2:
输入:
5
/ \
1 4
/ \
3 6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
根节点的值为 5 ,但是其右子节点值为 4 。示例3:
输入:
10
/ \
5 15
/ \
6 20
输出: false
解释: 输入为: [10,5,15,null,null,6,20]。
根节点的值为10,15的左结点6应该在根节点的左子树中 。题目理解
这道题依然是传入一个root根节点
我们先根据它实现好的指针结构还原整个二叉树
然后判断其是否为二叉搜索树
二叉搜索树的特点题目中已经给出,我们不过多阐述。
思路分析
参考第一道例题,我们是不是可以采用使用类似的递归方法
思考一下,我们遍历每一个节点,如果每一个非叶子节点(无子节点的节点)都满足node.left.val<node.val<node.right.val
我们就可以断定其为二叉搜索树了吗?
答案是否定的,我们看一下示例3,根节点10和它的右结点15都满足这样的条件,但是它并不是一个二叉搜索树,它不满足根节点10的右子树的所有节点的值都小于10。
这道题的关键所在就在于
除了遍历每一个节点都符合要求之外我们还需要严格控制递归的顺序
假设我们有一个层数为4的满二叉树(如图所示,1-15代表节点的val)
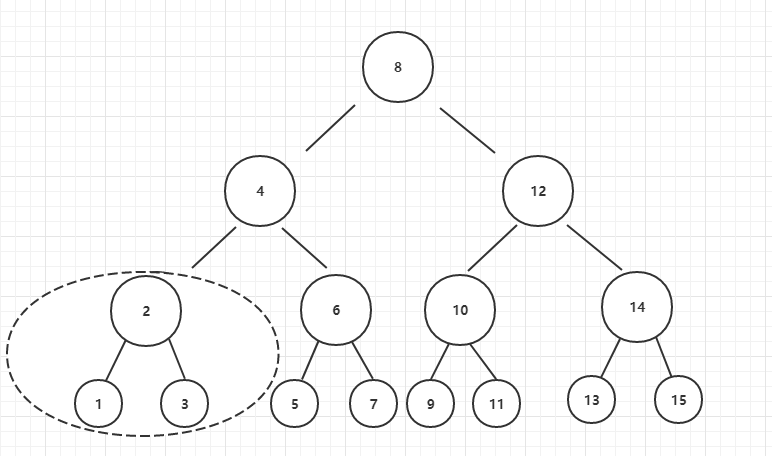
按照二叉搜索树的特点
- 每一个节点的左子树中所有节点值都小于该节点的值
- 每一个节点的右子树中所有节点的值都大于该节点
很明显,我们上方的二叉树满足了二叉搜索树的特点。
那么大家可以注意到,
该二叉树的节点值的从小到大的排列顺序就是图中的1-15
也就是说 满足这个排列规律的就是一个二叉搜索树
首先我们设置一个变量max,初始值为-Infinity,用来记录上次遍历节点的值
我们控制程序按照图中1-15的顺序递归,每递归到一个元素判断它是否大于max,若大于则将max更新,若每一个值都大于max,就可以断定它是满足二叉搜索树的结构。
在查看源码以前
我希望大家可以思考一下我们怎样才可以控制程序按照图中1-15的顺序进行递归
然后对比一下我们的方法是否一致。
代码实现
// root依然为根节点,二叉树结构已生成
root => {
// 用来记录当前最大值
let max = -Infinity
// map函数用来查看当前节点是否符合二叉搜索树结构
// @param{Object} 节点
let map = node => {
// 若结点为空, 返回true
if(!node){
return true
}
// 若有左节点 先递归左结点 left记录当前节点左子树是否符合二叉搜索树结构
let l = map(node.left)
// 判断当前节点值是否大于max
if(node.val > max){
max = node.val
}else{
return false
}
// 左子树递归完成且当前节点也递归完成后 递归右子树
let r = map(node.right)
// 左右子树都满足条件 返回true
return l && r
}
// 初始传入根节点
return map(root)
}总结
虽然这两道题我们都仅仅用十行左右的代码就实现了功能,但是我们却用了很长的篇幅来讲
解,一方面是为了让有些不熟悉这种数据结构的同学对它有一定的了解于认识,另一方面也是
让大家更加熟悉递归的用法,熟练使用递归是每个程序员必备的能力,希望我的博客能对你有
所帮助!
我只是一名小白,大家如果有更好的实现方法一定请在评论区多多指教。