零知识证明 | 2.什么是多项式盲计算？

2019-05-15 1,226 阅读2分钟

上一篇介绍了什么是同态隐藏。假设取 $E(x) = g^x$ ，则 $E(x+y)$ 可以通过 $E(x)$ 和 $E(y)$ 计算出来：

$E(x+y) = E(x) \cdot E(y)$

实际上，不仅仅支持加法，支持所有"线性组合"的同态隐藏，比如 $E(ax + by)$ ：

$E(ax+by) = g^{ax+by} = g^{ax} \cdot g^{by} = (g^x)^a \cdot (g^y)^b = E(x)^a \cdot E(y)^b$

需要注意的是，上面的加法和乘法运算都是模p运算。

假设现在有一个d次多项式 $P(X) = a_0 + a_1 \cdot X + a_2 \cdot X^2 + … + a_d \cdot X^d$ ，其中的系数 $a_0,…,a_d \in \{0, p-1\}$ 是Alice需要保护的秘密。根据上面的特性，我们可以计算出 $E(P(X))$ ：

$E(P(X)) = E(1)^{a_0} \cdot E(X)^{a_1} \cdot E(X^2)^{a_2} … \cdot E(X^d)^{a_d}$

现在Bob想来验证Alice是不是真的知道这些秘密，于是他决定随机指定一个数 $s$ ，要求Alice计算 $E(P(s))$ 等于多少。但是，Bob不想直接把 $s$ 的值告诉Alice，也就是说，这个 $s$ 是Bob的秘密。显然，这又需要一次同态隐藏，也就是说，Bob把下面这些值提供给Alice：

$E(s), E(s^2), E(s^3), …, E(s^d)$

然后Alice就可以根据上面的公式计算 $E(P(s))$ 的值：

$E(P(s)) = E(1)^{a_0} \cdot E(s)^{a_1} \cdot E(s^2)^{a_2} … \cdot E(s^d)^{a_d}$

最终的效果是：在Bob不知道P(X)中的系数是多少，而Alice也不知道s等于多少的情况下，完成多项式的验证。这就是所谓的"多项式盲计算"。

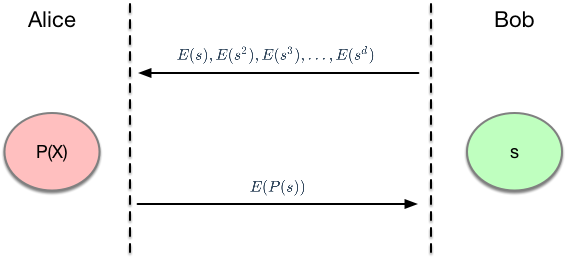
下面举个例子来加深理解，假设 $P(X) = 1 + 2X + 3X^2, E(x) = 3^x, p = 7$ ：

Bob想验证 $s=2$ 这一点上的 $E(P(s))$ 的值，那么他需要提供这2个值： $E(s) = 2, E(s^2) = 4$

然后Alice根据这3个值计算 $E(P(s))$ 的值然后返回给Bob：

$E(P(s)) = E(1)^1 \cdot E(s)^2 \cdot E(s^2)^3 = 3 \cdot 4 \cdot 64 |_{mod7} = 768|_{mod7} = 5$

最后，我们来看一下 $E(P(2))$ 是不是真的等于5：

$E(P(2)) = E(1 + 2 \cdot 2^1 + 3 \cdot 2^2) = E(17|_{mod6}) = E(5) = 3^5|_{mod7} = 243|_{mod7} = 5$

实际上，这背后依赖的理论基础是Schwartz-Zippel引理：在一个很大的集合中随机选择一组数，满足某个多项式取值的概率几乎为0。因此，随机选一个点，然后在Alice不知道该点的值的情况下，提供多项式的值以供Bob验证。

那么问题来了：Bob怎么验证Alice提供的 $E(P(s))$ 的值对不对呢？且听下回分解。