一道 LeetCode 的动态规划题的分析。
题目描述
题目来源 leetCode——53.最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
进阶: 如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的分治法求解。
动态规划
在分析如何使用动态规划求解该问题前,我们先简单了解下什么是什么是动态规划(DP)。
动态规划的适合解决的问题应该符合 “一个模型三个特征”。
一个模型
一个模型指的是 多阶段决策最优解模型。指的是要经历多个决策阶段,每个决策对应多个状态。然后我们从中找出一组能够产生最优解的决策序列。
三个特征
- 最优子结构
后面的决策可以通过前面的决策推导出。 比如说最经典的0-1背包问题,我们依次把物品放入背包(或不放入)背包。当进行到第 n 次决策(是否将第 n 个物品放入书包)时,前面的第 n - 1 已经决定好的多种决策(前面不同决策序列最终在 n - 1 次决策时给出了所有可以达到的重量),不会因为第 n 次的决策发生改变。
- 无后效性
一旦某个阶段 a 的决策结束后,后面阶段进行决策时,就不用考虑到阶段 a 是如何推导出来的。我们只需要用到它的最终得到的决策序列。
- 重复子问题
不同的决策序列,在到达第 n 次决策结束后,可能会产生重复的状态。比如假设依次要放入背包的物品的重量分别为 2、4、2、3。 我们进入决策是否放入第3个物品的阶段时,就会出现 “放入第1、3个物品和只放入第2个物品的两组决策序列达到相同的重量”。这就是重复的状态,可能会发生也可能不会发生。
动态规划的两种解题思路
1. 状态转移表法
动态规划能解决的问题,都可以用回溯法的暴力搜索解决。所以我们可以先用简单的回溯算法去试着去解决,从中找到规律,画出递归树。
当我们发现重复子问题时,一是可以使用 回溯+“备忘录” 的方法。所谓备忘录,就是我们会把 f(n) 的结果用散列表保存起来(回溯经常用到递归函数),当又一次调用 f(n) 时,就直接取出缓存起来的结果,以减少重复计算。二是这里说的 状态表转移表法。
通常状态表是二维度的。每行代表着每一个阶段决策后的多个状态。这个二维数组会一行一行地进行填充,直到达到满足结束状态的情况(比如0-1背包问题就是重量刚好达到背包最大承重,或者n个物品都进行了决策,即完成了第 n 次决策)。这时我们只需要从最终的阶段找出最终结果即可(背包问题是从后往前找出一个重量最大的值)
2. 状态转移方程法
关键在于找出 状态转移方程。根据最优子结构,写出递归公式,也就是所谓的状态转移方程。
动态规划解法
那么我们开始着手分析问题了。
首先我们试着用 状态转移表法 来做这道题。
以 [-2,1,-3,4,-1,2,1,-5,4] 为例进行分析,我们画个递归树分析一下。
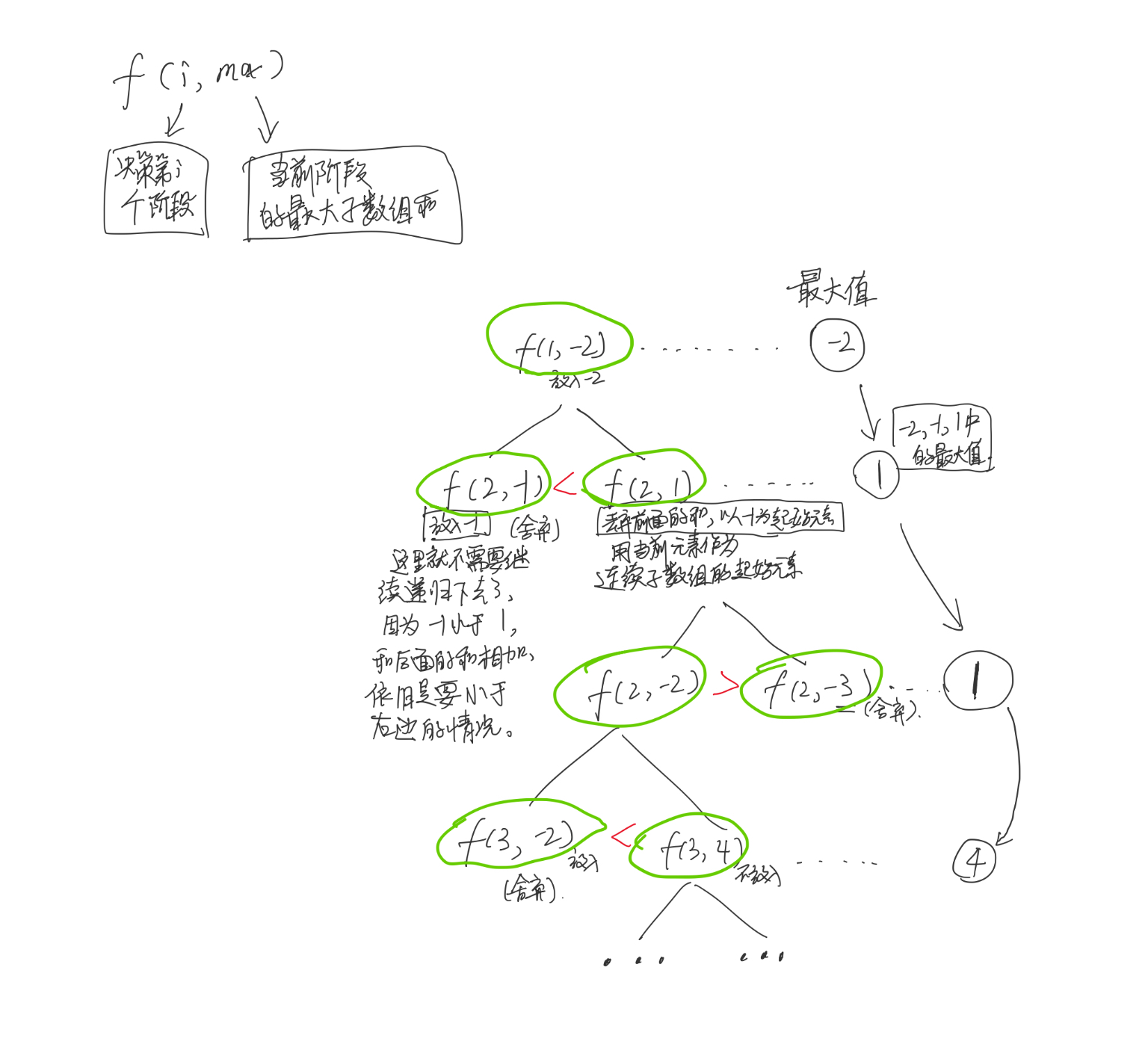
(i, sum)。i 代表 第 i 个阶段的决策,具体做的决策是:是选择当前的元素为新的子数组的起点,还是让当前元素作为原来子数组的后继数组元素。具体逻辑如下图:
每个阶段我们都会拿到决策后的两种连续子数组的和,我们会把它们和上一次阶段的最大和比较,取出最大的值。
这里要注意的是,当我们要选择决策后的两种情况的其中一种情况和大的情况,进行下一次遍历,另一种情况是不需要进行下次的递归的。因为总和小的情况下的数组,和后面的数组相加时,必然比总和大的情况的总和要小,所以不需要进行接下来的递归。
js 代码实现
var maxSubArray = function(nums) {
// 动态规划
let len = nums.length;
let max = nums[0];
let prevSum = nums[0];
for (let i = 1; i < len; i++) {
prevSum = Math.max(nums[i], prevSum + nums[i]);
max = Math.max(max, prevSum);
}
return max;
};