自然语言基础-语言模型

2019-05-20 353 阅读2分钟

LANGUAGE MODELING TASK

什么是 LM 任务？

计算一句话出现的概率

P\left(w_{1 : n}\right)=P\left(w_{1}\right) P\left(w_{2} | w_{1}\right) P\left(w_{3} | w_{1 : 2}\right) P\left(w_{4} | w_{1 : 3}\right) \ldots P\left(w_{n} | w_{1 : n-1}\right)

计算一系列单词之后出现的下一个单词的概率

p\left(w_{i} | w_{1}, w_{2}, \ldots, w_{i-1}\right)=\frac{p\left(w_{1}, w_{2}, \ldots, w_{i-1}, w_{i}\right)}{p\left(w_{1}, w_{2}, \ldots, w_{i-1}\right)}

可以看到上面的方法在预估条件概率时，使用的是统计值，即数据量足够多时，统计值接近去真实概率值。

根据马尔科夫假设，我们可以将条件概率进行简化，单词的条件概率只和前面的k个词有关：

P\left(w_{i+1} | w_{1 : i}\right) \approx P\left(w_{i+1} | w_{i-k : i}\right)

P\left(w_{1 : n}\right) \approx \prod_{i=1}^{n} P\left(w_{i} | w_{i-k : i-1}\right)

k阶的语言模型受限于模型复杂度，当样本特别大时，为了解决计算成本，我们只能减小k，而为了打破马尔科夫假设，现在有了注意力模型，能够对更多的前序单词进行建模。

n-gram 语言模型的两个主要问题

Sparsity

传统计算条件概率的方法是统计方法

\hat{p}_{\mathrm{MLE}}\left(w_{i+1}=m | w_{i-k : i}\right)=\frac{\#\left(w_{i-k : i+1}\right)}{\#\left(w_{i-k : i}\right)}

统计出来的值等于真实概率的条件是样本足够多，那可能的问题有： $\#\left(w_{i-k : i+1}\right)$ 可能在训练集中从没出现，那这个值就是0，那概率就是0。那避免zero-probability 0概率的方法就是使用平滑技术（smoothing techniques），最常见的平滑方法是： $\mathrm{add}-\alpha$

\hat{p}_{\mathrm{add}-\alpha}\left(w_{i+1}=m | w_{i-k : i}\right)=\frac{\#\left(w_{i-k : i+1}\right)+\alpha}{\#\left(w_{i-k : i}\right)+\alpha|V|}

其中 $|V|$ 是词典大小， $0<\alpha<=1$ .

另外一种平滑方法是：back-off

\hat{p}_{\mathrm{int}}\left(w_{i+1}=m | w_{i-k : i}\right)=\lambda_{w_{i-k : i}} \frac{\#\left(w_{i-k : i+1}\right)}{\#\left(w_{i-k : i}\right)}+\left(1-\lambda_{w_{i-k : i}}\right) \hat{p}_{\mathrm{int}}\left(w_{i+1}=m | w_{i-(k-1) : i}\right)

目前最好的平滑方法是：Kneser-Ney。

Storage

我们需要记录所有所有n-gram的数，随着n增加，模型参数急剧变大。

神经网络模型

rnn

模型图：

公式描述：

h_{t}=\sigma\left(W^{(h h)} h_{t-1}+W^{(h x)} x_{t}\right)

\hat{y}_{t}=\operatorname{softmax}\left(W^{(S)} h_{t}\right)

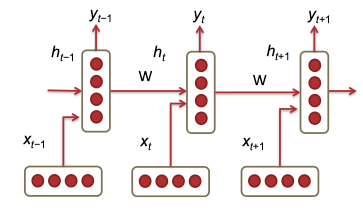
其中

$x_{1}, \ldots, x_{t-1}, x_{t}, x_{t+1}, \ldots x_{T}$ 是每个时刻的输入向量
，t时刻的状态根据t-1时刻状态和输入计算出来
- $x_{t} \in \mathbb{R}^{d}$
- $W^{h x} \in \mathbb{R}^{D_{h} \times d}$
- $W^{h h} \in \mathbb{R}^{D_{h} \times D_{h}}$
- $h_{t-1} \in \mathbb{R}^{D_{h}}$
- $\sigma( )$ 非线性函数，此处是 sigmoid
:根据hidden计算输出
- $W^{(S)} \in \mathbb{R}^{|V| \times D_{h}}$
- $\hat{y} \in \mathbb{R}^{|V|}$

我们可以看到模型中最主要的参数是最后一层的 $W^{S}$ ，随着vocabulary size的增加， $W^{S}$ 的大小越来越大。

rnn 模型的 loss

t时刻的loss

J^{(t)}(\theta)=-\sum_{j=1}^{|V|} y_{t, j} \times \log \left(\hat{y}_{t, j}\right)

总loss为时刻t累加:

J=\frac{1}{T} \sum_{t=1}^{T} J^{(t)}(\theta)=-\frac{1}{T} \sum_{t=1}^{T} \sum_{j=1}^{|V|} y_{t, j} \times \log \left(\hat{y}_{t, j}\right)

语言模型的困惑度定义：

\text { Perplexity }=2^{J}

rnn 模型的优缺点

优点
- 可以处理任意长度的时序数据
- 通过传递hidden state，可以利用t时刻之前的数据
缺点
- 计算慢，t时刻的状态依赖于t-1时刻，只能串行计算
- 实际训练过程中，由于梯度消失/爆炸问题，很难利用很早之前的信息

梯度消失/爆炸问题

rnn模型的一个目标是：能够将hidden state传播下去，但是在实际中会出现梯度消失/爆炸问题，下面我们以一个例子来说明这个问题：例子：

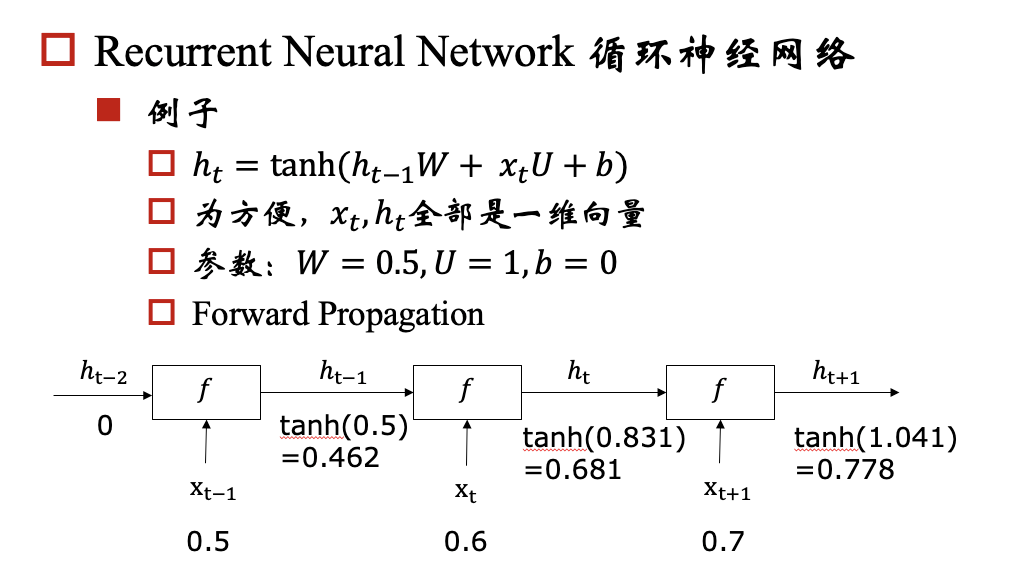
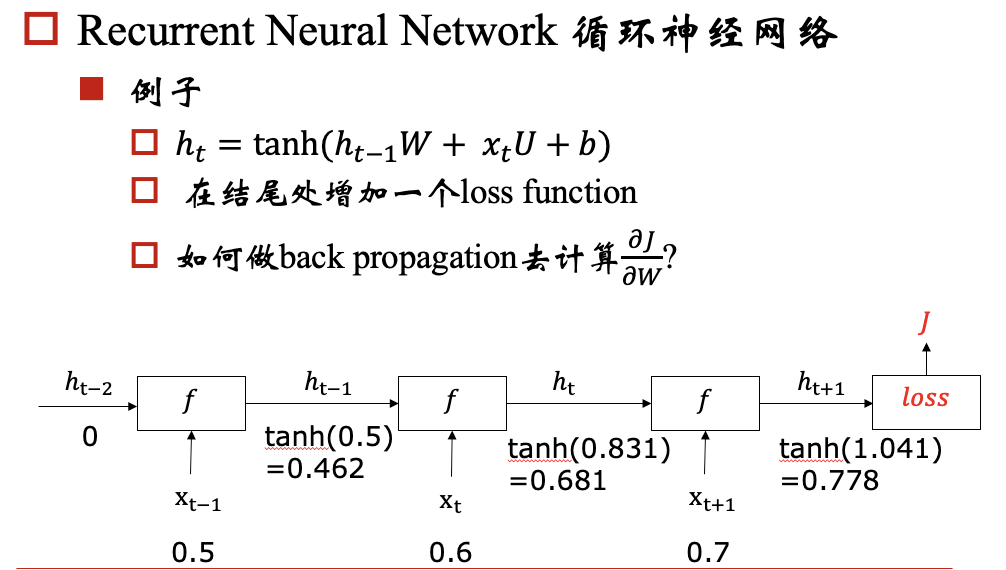
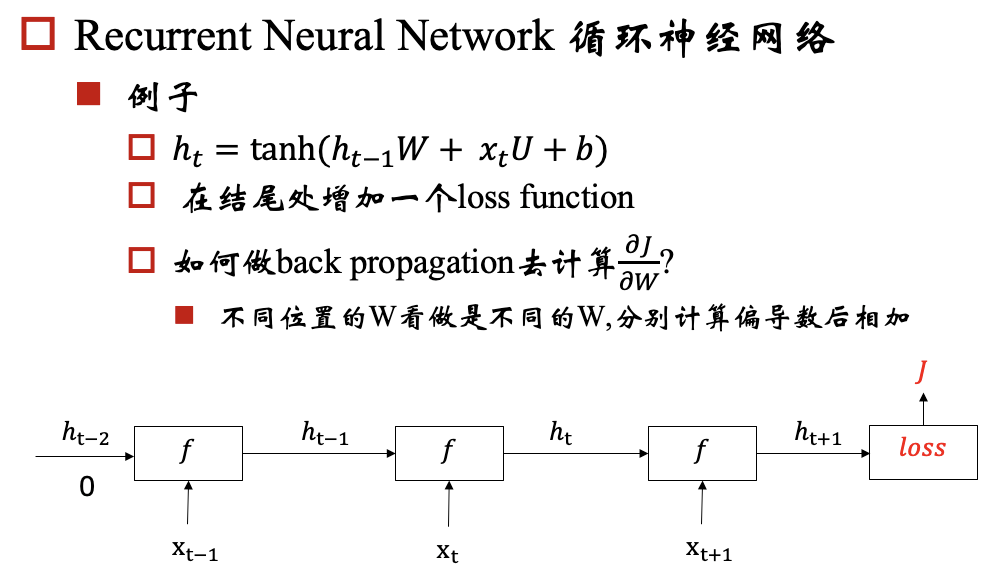
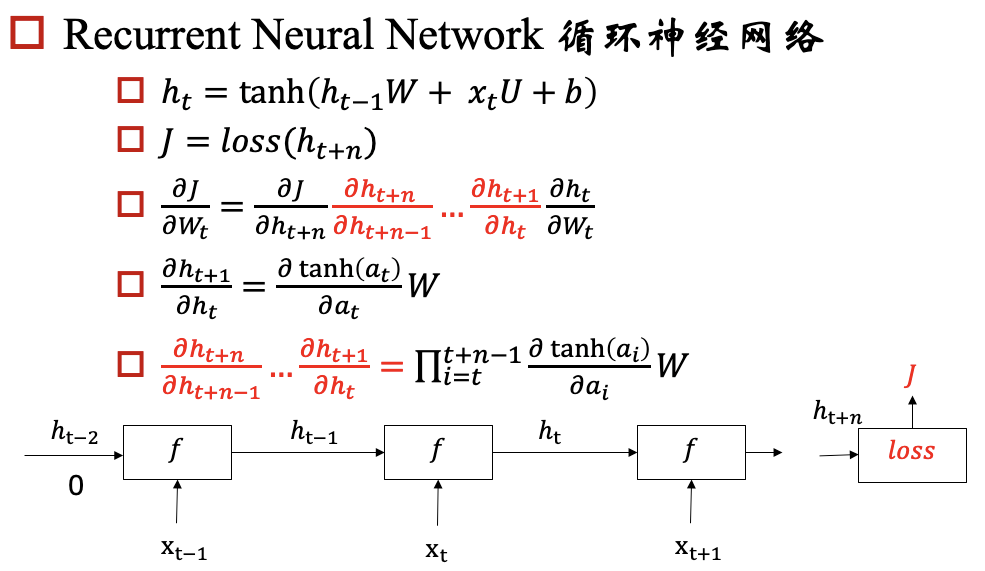
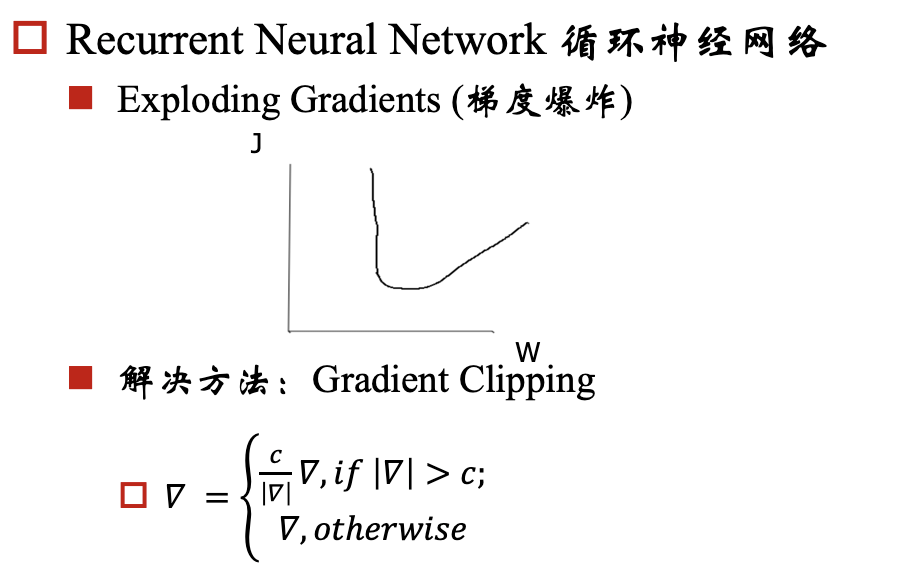
对于梯度爆炸问题，我们可以通过 Gradient Clipping来解决，对于梯度消失问题呢？我们要保证反向传播的时候，梯度不能过小，那我们就期望对于每个 $\frac{\partial h_{t+1}}{\partial h_{t}}$ 都尽可能接近于1，那相乘的时候，就不会变小了。

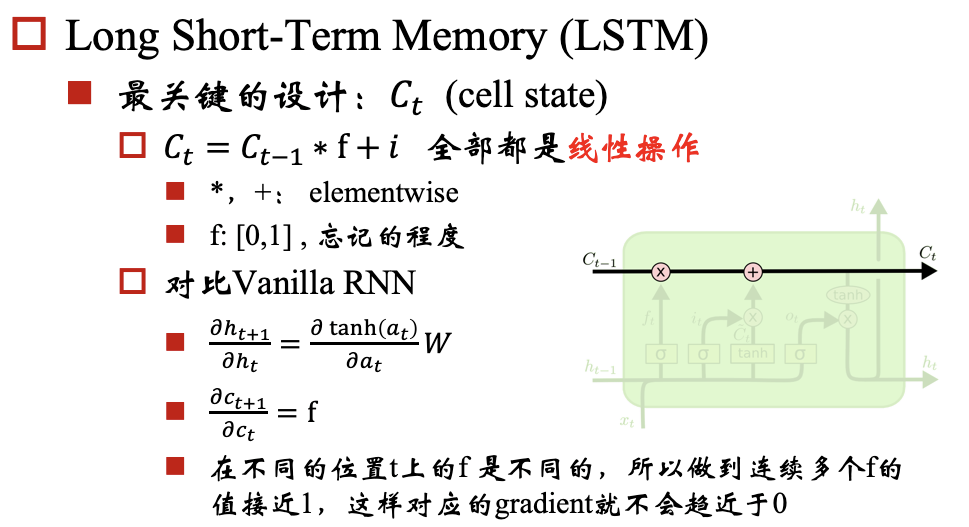
建议先读关于LSTM的文章：Understanding LSTM Networks

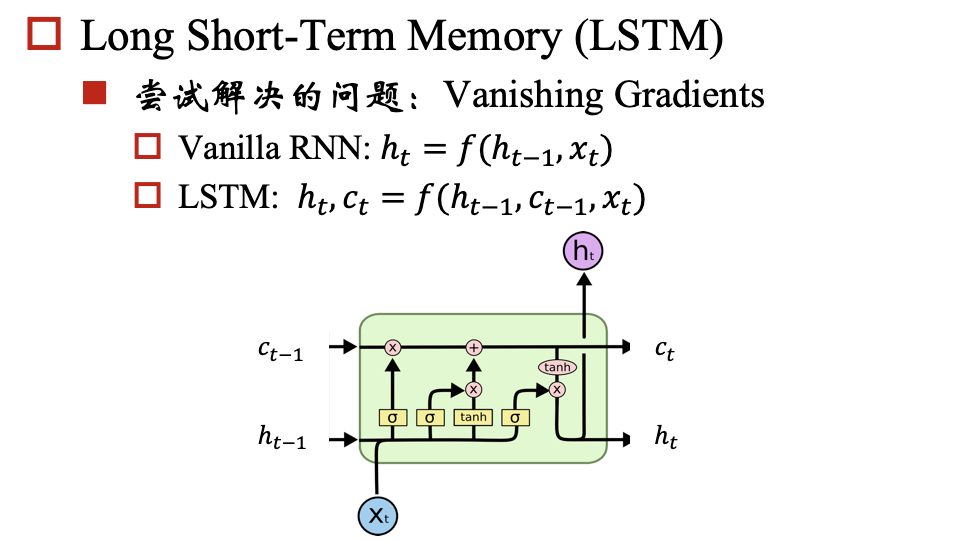
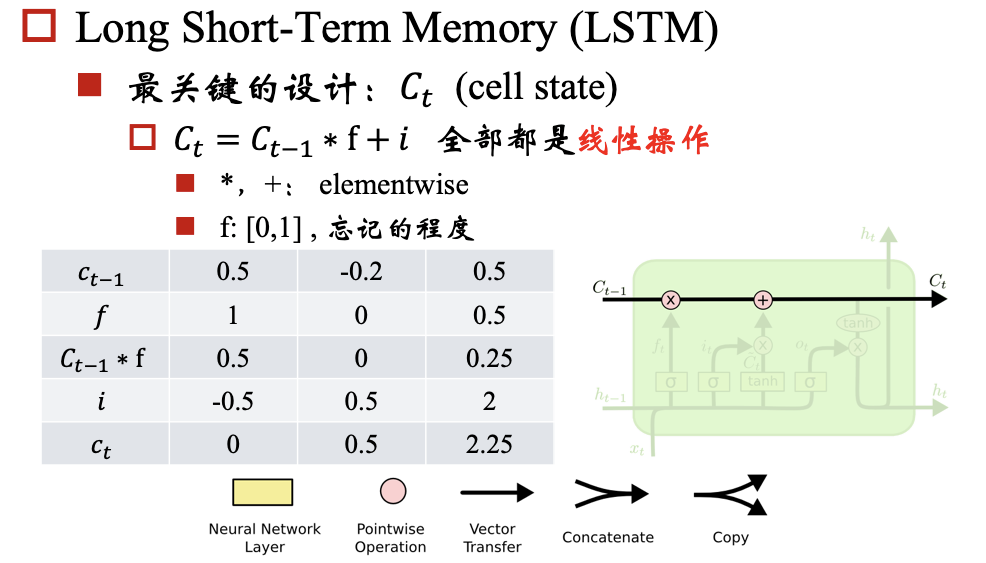
##参考

github.com/zhuanxuhit/…

web.stanford.edu/class/cs224…

友情链接：