以下内容总结自极客时间王争大佬的《数据结构与算法之美》课程,本文章仅供个人学习总结。
上一个文章主要是讲了几种计算时间复杂度的几个法则:
- 只看循环次数最多的代码
- 加法法则:总复杂度等于量级最大的那段代码的复杂度
- 乘法法则:嵌套代码的复杂度等于嵌套内外复杂度的乘积
常见的时间复杂度,由低到高排序:
、
、
、
、
、
、
、
接下来介绍一下几种新的复杂度:
最好、最坏情况时间复杂度
function find(array, n, x) {
let pos = -1;
for (let i = 0 ; i < n; ++i) {
if (array[i] === x) {
pos = i;
}
}
return pos;
}
上面的代码是用来在数组中寻找变量x出现的位置,如果没有找到就返回-1,我们一眼能看出代码的时间复杂度为。但是这个代码是可以优化的,因为可能中途就找到了这个元素,就不需要继续后面的循环了。所以我们改一下代码
function find(array, n, x) {
let pos = -1;
for (let i = 0 ; i < n; ++i) {
if (array[i] === x) {
pos = i;
break;
}
}
return pos;
}
修改完毕后,这个函数的时间复杂度还是吗?不一定把,因为都不一定会执行n次,可能数组的第一个元素就是x,也可能数组的第n个元素为x,那么这两种情况一个执行一次,一个执行n次。所以就有了最好时间复杂度、最坏时间复杂度,顾名思义就是最理想情况下的复杂度和最不理想下的时间复杂度,对应到上面的find函数,最好时间复杂度就是
,数组第一个元素就是x,最坏时间复杂度为
平均时间复杂度
最好时间复杂度和最坏时间复杂度都是极端情况下的代码复杂度,这种情况比较少,发生的概率并不大。为了更好的表示平均情况,于是有了平均时间复杂度。 平均时间复杂度的分析方式,还是以上面的例子分析。
function find(array, n, x) {
let pos = -1;
for (let i = 0 ; i < n; ++i) {
if (array[i] === x) {
pos = i;
break;
}
}
return pos;
}
要查找的变量x在数组中的位置有n+1种情况:0 ~ n-1 和不在数组中,将每一种情况需要循环的次数加起来,除以n+1就得到了平均需要遍历的元素个数。
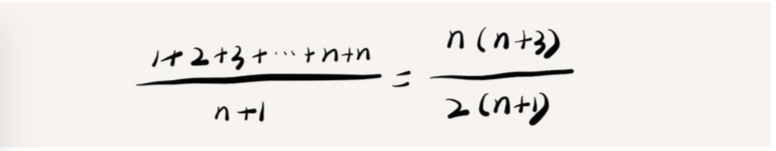
很明显并不一样,我们假设x在数组中和不再数组中的概率55开,都为 ,然后在0 ~ n-1的范围每个地方出现的概率为
,根据乘法法则在数组中并且在0 ~ n-1中每个地方出现的概率是
。于是计算公式就成了
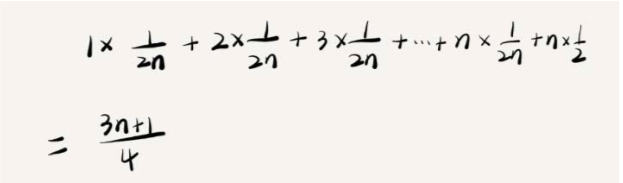
均摊时间复杂度
其实均摊时间复杂度个人理解是平均时间复杂度的一种,均摊时间复杂度分析起来更加简单,不需要像上面的平均时间复杂度那么复杂的计算,而是通过找规律直接计算出时间复杂度。怎么找规律呢?下面用一个例子来分析。
let array = new Array(n);
let count = 0;
function insert(val) {
if (count === array.length) {
let sum = 0;
for (let i = 0; i<array.length; i++) {
sum = sum + array[i];
}
array[0] = sum;
count = 1;
}
array[count] = val;
++count;
}
这段代码实现了一个往数组中插入数据的功能。当数组满了之后,也就是代码中的count == array.length时,我们用for循环遍历数组求和,并清空数组,将求和之后的sum值放到数组的第一个位置,然后再将新的数据插入。但如果数组一开始就有空闲空间,则直接将数据插入数组。
我们分析以下这段代码的时间复杂度
- 最好时间复杂度:数组中有空闲空间,直接插入下标为count的位置就可以了,所以最好时间复杂度为
- 最坏时间复杂度:数组中没有空闲空间,需要对数组进行一次遍历求和然后插入,所以最坏时间复杂度为
- 平均时间复杂度(期望时间复杂度):假如数组长度为n,当数组存在空闲空间时,根据插入位置分为n种情况,每种情况的时间复杂度为
,除此之外,还有一种“额外”的情况,就是在数组没有空 闲空间时插入一个数据,这个时候的时间复杂度是O(n)。而且,这n+1种情况发生的概率一样,都是1/(n+1)。所以,根据加权平均的计算方法,我们求得的平均时 间复杂度就是:
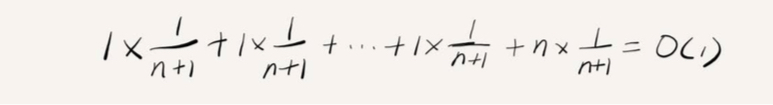
的插入操作后,此时数组满了,执行一次
的求和和清空操作。这样的话其实前面的n个
和1个
其实是可以抵消掉的,这种抵消的方法叫摊还分析法,通过摊还分析法得到的时间复杂度也叫均摊时间复杂度,在这里得到的就是
总结 一、复杂度分析的4个概念
1.最坏情况时间复杂度:代码在最理想情况下执行的时间复杂度。
2.最好情况时间复杂度:代码在最坏情况下执行的时间复杂度。
3.平均时间复杂度:用代码在所有情况下执行的次数的期望值表示。
4.均摊时间复杂度:在代码执行的所有复杂度情况中绝大部分是低级别的复杂度,个别情况是高级别复杂度且发生具有时序关系时,可以将个别高级别复杂 度均摊到低级别复杂度上。基本上均摊结果就等于低级别复杂度。
二、为什么要引入这4个概念?
1.同一段代码在不同情况下时间复杂度会出现量级差异,为了更全面,更准确的描述代码的时间复杂度,所以引入这4个概念。
2.代码复杂度在不同情况下出现量级差别时才需要区别这四种复杂度。大多数情况下,是不需要区别分析它们的。
课后思考题
分析下面add函数的时间复杂度
let array = new Array(10);
let len = 10;
let i = 0;
function add(element) {
if(i >= len) {
// 申请两倍长度的数组空间
let new_array = new Array(len*2);
for(let j = 0; j < len; j++) {
// copy原来的array,到new_array中
new_array[j] = array[j];
}
// array大小为2倍len
array = new_array;
len = 2*len;
}
// element放在下标为1的位置,下标i加1
array[i] = element;
++i;
}
- 最好时间复杂度:数组没满,直接设置
array[i]=element, 此时最好时间复杂度为 - 最坏时间复杂度:数组满了,需要copy原来的数组,循环len次,所以最坏时间复杂度为
- 平均时间复杂度(期望时间复杂度):
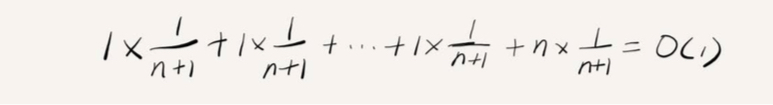
- 均摊时间复杂度:前n个操作为
,后一个为
,所以抵消后得到时间复杂度为