
以下内容总结自极客时间王争大佬的《数据结构与算法之美》课程,本文章仅供个人学习总结。
数组,是日常开发中用到的最多的数据结构之一,自己一度认为数组太简单了,不就是通过下标拿元素,遍历数组,查找排序等操作。对数组的理解太浅显了,直到看了大佬对数组的介绍,才发觉自己真是坐井观天,今日就来聊一聊数组。
数组专业一点来说是属于“线性表”的一种,它用一组连续的内存空间来存储具有相同类型的数据。
常见的线性表结构有链表、数组、栈、队列,顾名思义线性表就是数据排列在一条线上,每个线性表上的数据最多只有前后两个方向。
非线性表结构则比线性表更复杂,非线性表上的数据并不是简单的前后关系,常见的非线性表数据结构有图、树、堆等。
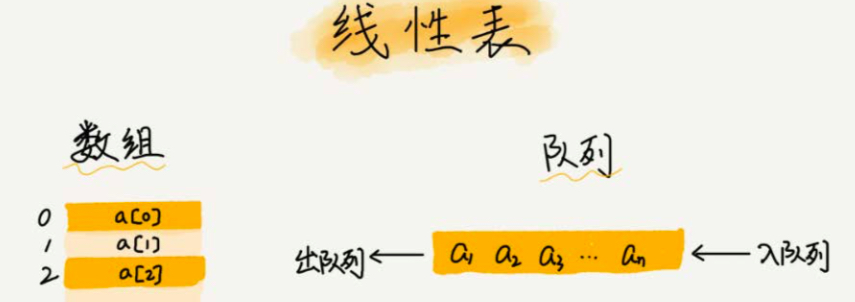
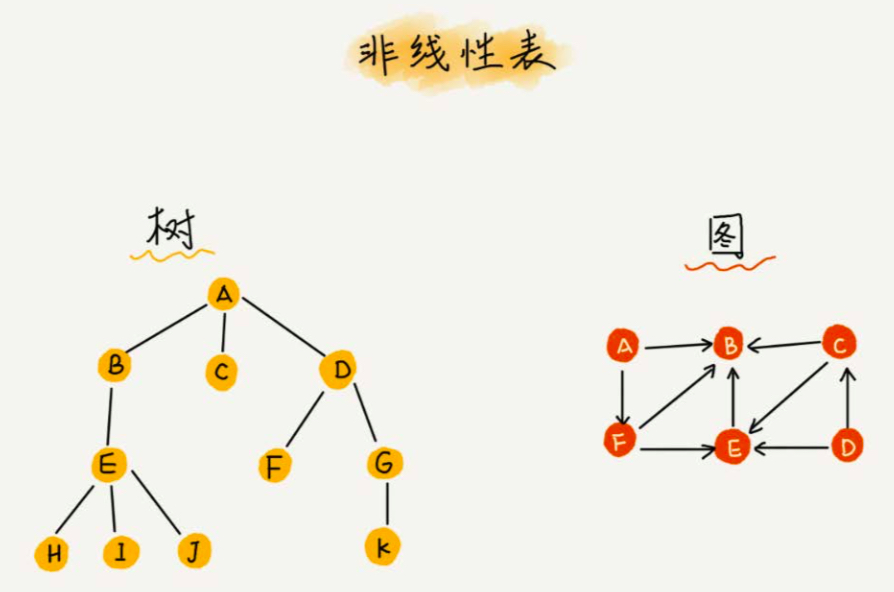
通过上面的图,我们能明显看到线性表和非线性表的不同之处。线性表只有前后关系,非线性表则存在多种关系。
继续说数组,上面说到来数组是线性表的一种,并且数组是连续的内存空间,相同的数据类型,所以数组有通过下标“随机访问”的特性,但是这也带来了一些弊端,就是数组是连续的,导致删除和插入的时候为了保证连续性需要进行大量的数据迁移。
数据的访问,那到底数组是怎么通过下标随机访问元素的呢?
拿一个长度为10的int类型数组 int[] a = new int[10]; 计算机会给数组分配连续的内存空间 1000~1039,其中内存首地址为base_address = 1000;
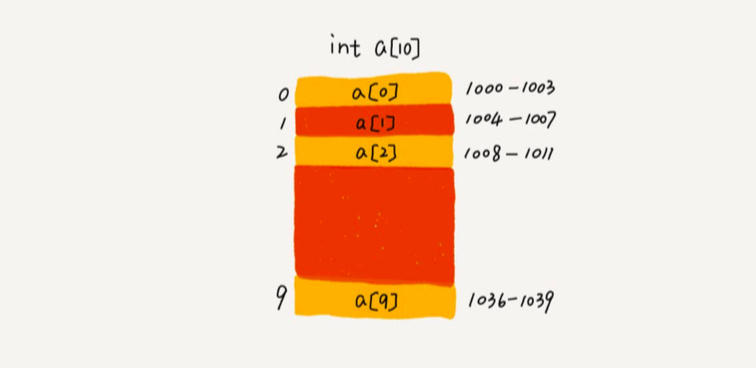
我们知道计算机会给每个内存单元分配一个地址,计算机通过这个内存地址访问内存中的数据。数组中由于内存是连续的,所以我们可以通过基地址直接计算出对应的下标所在的内存地址。数组中计算某个下标元素的内存地址公示如下:
a[i]_address = base_address + i * data_type_size
在本例子中,数组中存储的是int类型数据(js中数组每个元素大小可以不同,是做了特殊处理,js中具体数组在内存中如何存储待研究,所以这里用java中的数组来讲),data_type_size为4个字节,所以如果要获取下标为2的元素的地址,通过上面的公式计算就得到来内存地址为1008,由于只计算一次就能获取到准确的内存地址,所以访问数组中某个元素的时间复杂度为
低效的“插入”和“删除”
为什么说数组的“插入”和“删除”操作很低效呢?我们知道数组在内存中是连续的,如果进行插入或者删除操作的话,由于数组要保证内存数据的连续性,所以数据需要进行移动,来保证连续性。
下面举例说明:
插入:
插入操作:假设数组的长度为n,现在,如果我们需要将一个数据插入到数组中的第k个位置。为了把第k个位置腾出来,给新来的数据,我们需要将第k~n这部分的元素都顺 序地往后挪一位。那插入操作的时间复杂度是多少呢?我们可以分析一下。
分析:如果第k个位置是数组末尾,那么不需要移动数据,此时最好时间复杂度为。如果在数组的开头插入数据,则所有的数据都要往后移动一位,所以最坏时间复杂度为
。因为我们在每个位置插入的元素的概率是一样的,所以平均时间复杂度为
通过上面的分析我们看到,插入操作的平均时间复杂度为,那么有没有能够优化的地方呢?其实是有的,但是只能针对特定的情况进行优化。比如当数组仅仅作为存储数据的集合而不在乎存储的数据的顺序时,我们可以直接将第k个元素放在数组最后,将要插入的元素放在第k个位置。这样就能做到时间复杂度为
,这也是快排的思想之一,但这也导致了快排是一个不稳定的排序算法关于排序算法稳定性的介绍
举个例子来看一下上面的优化方式:假设数组a[10]中存储了如下5个元素:a,b,c,d,e。 我们现在需要将元素x插入到第3个位置。我们只需要将c放入到a[5],将a[2]赋值为x即可。最后,数组中的元素如下: a,b,x,d,e,c。如下图所示
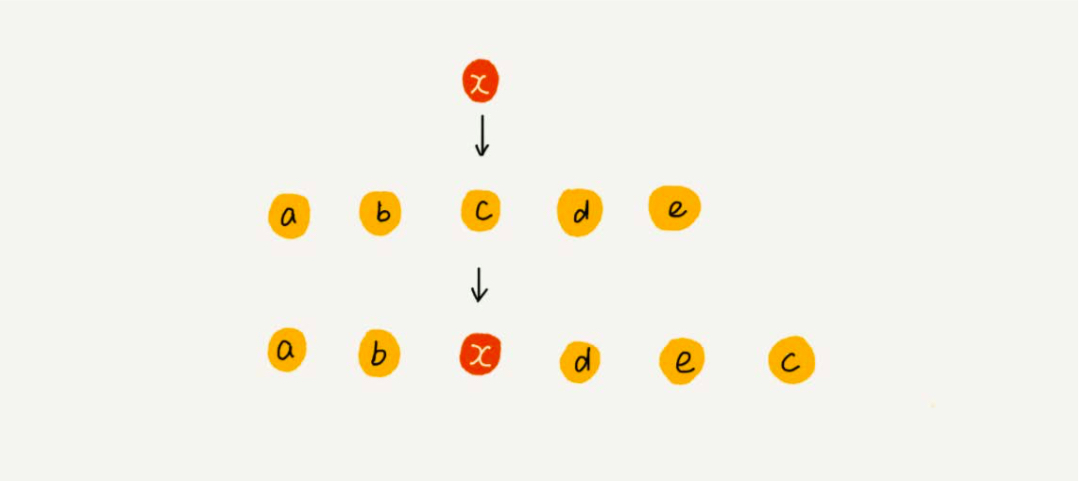
删除:
删除操作:存在长度为n的数组,现在需要删除第k个元素,删除第k个元素后为了保证数组中第k个位置不出现空洞导致数组内存不连续,所以需要将k~n的元素都要向前移动一位。我们依旧分析一下时间删除操作的时间复杂度。
分析:如果删除的是最后一个元素,则不需要移动,所以最好时间复杂度为,删除的是第一个元素,那么后面的k~n个元素都要向前移动一位,所以最坏时间复杂度为
,在每个位置删除的概率是一样的,那么平均时间复杂度为
那么删除操作能否优化呢?其实也是可以的,我们通过上面的例子知道每删除一个元素就要移动后面的所有元素,那么我们能不能把多个删除操作放在一起,统一进行一次数据移动呢?
举个例子来看一下上面的优化方式:数组a[10]中存储了8个元素:a,b,c,d,e,f,g,h。现在,我们要依次删除a,b,c三个元素。
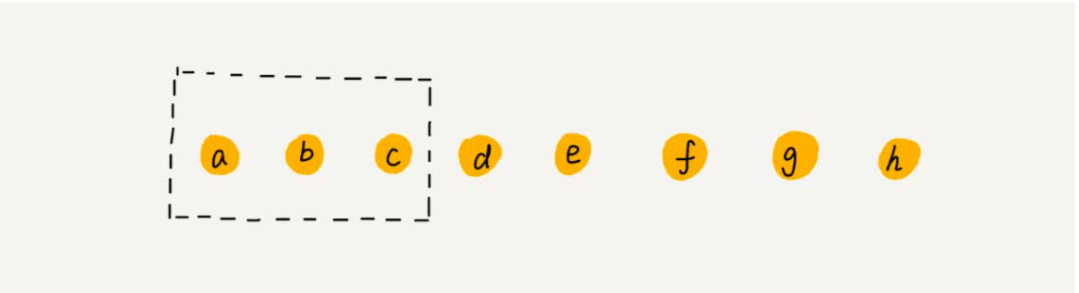
如果你了解JVM,你会发现,这不就是JVM标记清除垃圾回收算法的核心思想吗?没错,数据结构和算法的魅力就在于此,很多时候我们并不是要去死记硬背某 个数据结构或者算法,而是要学习它背后的思想和处理技巧,这些东西才是最有价值的。如果你细心留意,不管是在软件开发还是架构设计中,总能找到某些算 法和数据结构的影子。 --王争
解答标题,为什么很多编程语言中数组下标都是从0开始
我们之前有计算过数组的内存寻址公式 a[i]_address = base_address + i * data_type_size,如果从1开始的话,我们可以得到对应的内存寻址公式为 a[i]_address = base_address + (i - 1) * data_type_size,每次随机访问一个元素都多了一个减法操作。
数组是一种很基础的数据结构,效率需要尽可能的高,所以为了减去一次减法操作,所以数组选择了从0开始编号而不是从1开始。
当然也并不是非0不可,有的语言甚至支持负数的下标,例如python。但是大多数都是从0开始编号,可能也和C语言以0作为下标有关,后面的语言或多或少的都借鉴了C语言。
内容小节
我们今天学习了数组。它可以说是最基础、最简单的数据结构了。数组用一块连续的内存空间,来存储相同类型的一组数据,最大的特点就是支持随机访问,但 插入、删除操作也因此变得比较低效,平均情况时间复杂度为O(n),我们也了解到了一维数组的寻址公式,和插入和删除操作的优化方法。
思考
一维数组寻址公式我们已经知道了a[i]_address = base_address + i * data_type_size,那么二维数组的寻址公式呢?在留言处写下你的答案把!