这谁顶得住啊，数学运算原来是这样实现的

1+1等于多少？我们可以脱口而出2！那么复杂一点的运算呢？比如(1 +（2 + 3）* 4 + ( 5 - 6 ) / 1)是多少？这时候我们可能就要稍微思考一下，脑中浮现出小学时候数学老师教给我们的运算法则和规律，先计算括号中的，然后计算乘法除法。emememem...一顿操作之后我们得出答案20。思考一下我们计算这个数学答案需要有这么多步骤，那么计算机是怎么计算的呢？它总不可能跟我们人一样来一发孩提时期的思考吧？

怀着这么疑问，我们来进行探索。

接下来的一下代码是java相关的，其他语言方向朋友如果身体不慎可以跳过java代码部分阅读结论部分。

作为一个java程序员，既然我们要研究这个问题，那么我们是不是要立马打开编辑器来一顿hello word操作。写下如图的方法：

有人会问了，你写这个方法我能看出个什么鬼？当然不是了，我们需要了解一下jvm是怎么处理这段代码的。接下来进行javac 和 javap 操作，然后我们贴出该方法的字节码部分。

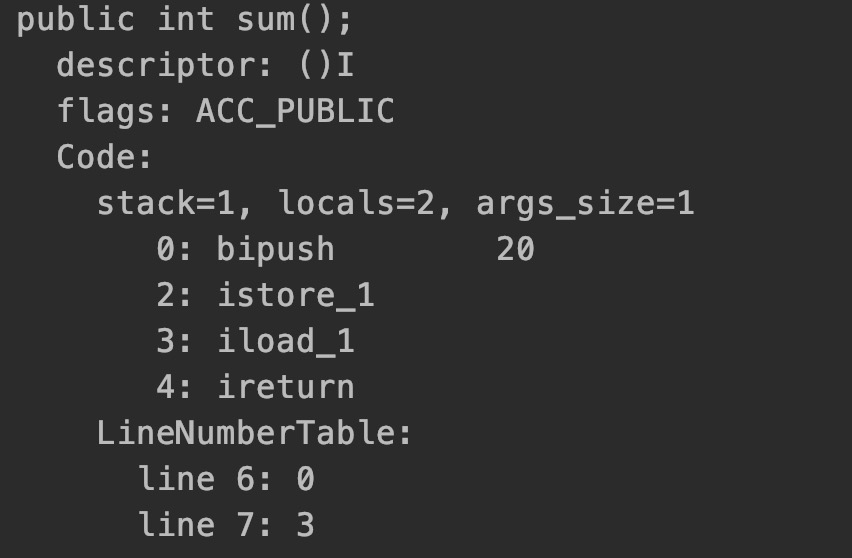
这行图我们来关注Code部分内容，突然发现代码中的1、2、3、4、5相关数字都没有了，直接出现了答案20。原来在javac时候，会对我们的代码进行优化，在编译时期就计算出答案直接将答案输出在class文件中从而减少jvm的计算量。这里由于水平原因我们就不看javac的代码实现了（看了也看不懂，还得理解半天），那么换一种思路，如下图：

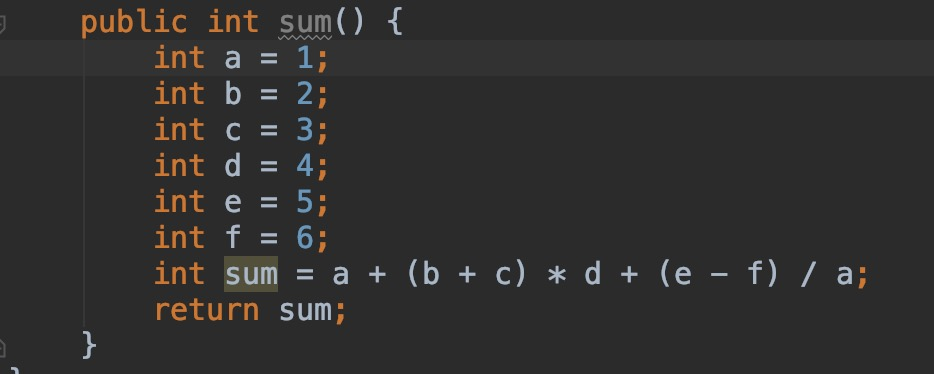
改良后的代码如下，用变量来声明数字，然后进行javac javap 看看会有什么产物，如下图：

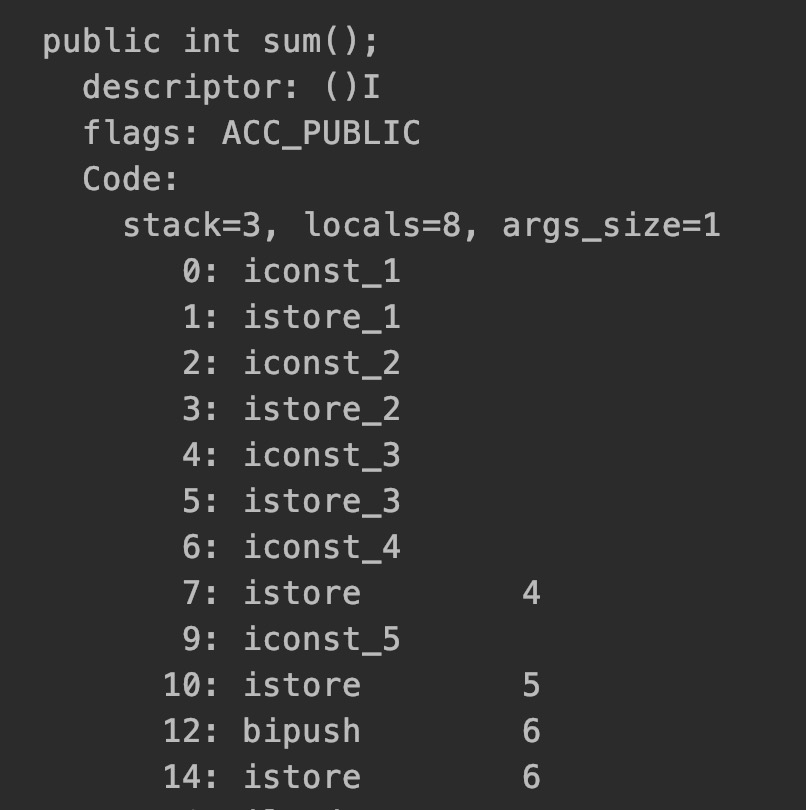
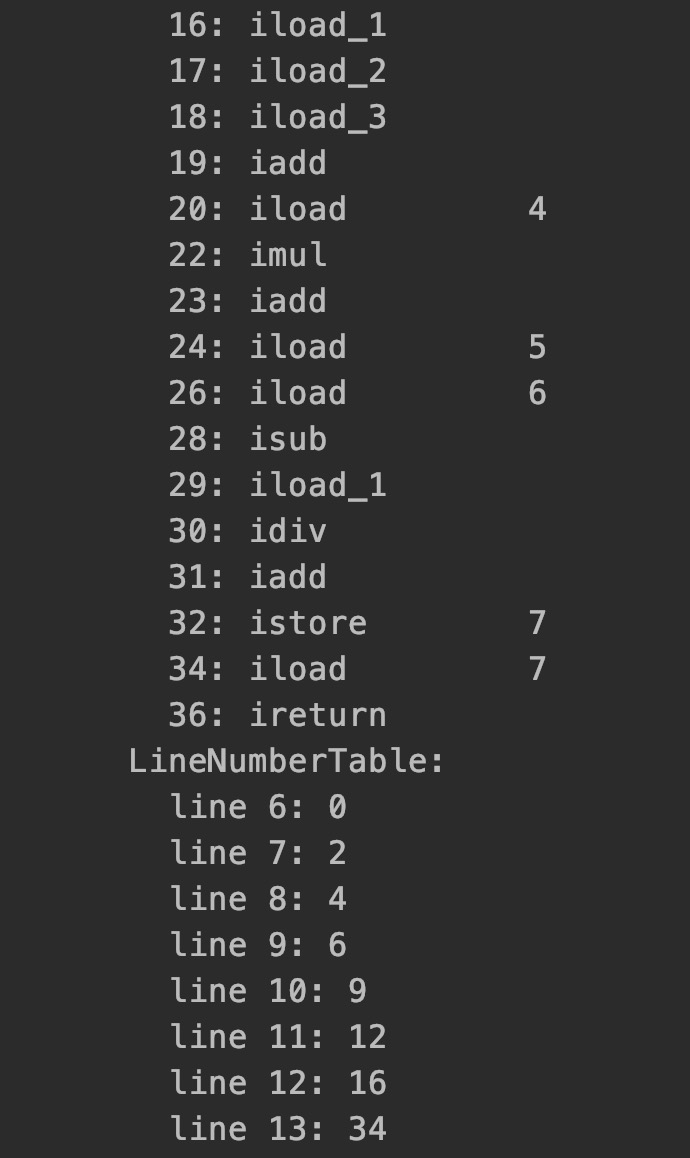
这里由于代码太长，所以分开来截图，接入下来进行相关的字节码分析。

还是只看Code部分内容：先看上半张图，第0行字节码iconst_1的大致意思就是将int 1 压入操作数栈，第1行字节码istore_1的大致意思是将操作数栈栈顶的元素1放入局部变量表的位置1中。其实对应的代码就是int a = 1。之后的几行代码也是类似的意思，同时在下半张图的局部变量表LineNubmerTable可以看出。

上半张图分析完毕，重头戏来了。下半部分的字节码就是运算部分，相关字节码表达的意思这里就不解释了，各位朋友可以百度一下。我这里写出字节码翻译之后的内容，也就是：1 2 3 + 4 * + 5 6 - 1 / +。waht？？？这输出的是啥玩意，靠这些东西怎么去得出最后的答案？

这些输出的符号叫做后缀表达式，同时也叫做逆波兰表示。

后缀表达式的规则：

从左到右遍历表达式的每个数字和符号，遇到数字就进栈，遇到是符号就将处于栈顶两个数字出栈，进行运算，运算结果进栈，一直到最终结果。

得到规则后下面来使用这些规则来进行相关计算：

首先初始化一个空栈，用来进行相关运算。
前三个数字是 1 2 3，我们将这三个哥们都进行入栈操作。这时候栈内元素有 1 2 3。
接下来是 + ，所以将 2 3 出栈，然后 2 + 3 等 5，将 5 入栈。这时候栈内元素有1 5。
接下来是 4 ，将 4 入栈。这时候栈内元素有 1 5 4。
接下来是 * ，按照规则将 4 5 出栈，然后 4 * 5 得 20，将 20 入栈。这时候栈内元素有 1 20。
接下来是 + ，将 1 20 出栈，1 + 20 等 21，将 21 入栈。这时候栈内元素有 21 。
接下来是 5 6 ，将 5 6 入栈。这时候栈内元素有 21 5 6。
接下来是 - ，将 5 6 出栈，5 - 6 等 -1 ，将 -1 入栈。这时候栈内元素有 21 -1。
接下来是 1 ，将 1 入栈，这时候栈内元素有 21 -1 1。
接下来是 / ，-1 1 出栈， -1 / 1 得 -1，将 -1 入栈。这时候栈内元素有 21 -1。
接下来是 + ，将 21 -1 出栈， 21 - 1 等 20，将 20 入栈。这时候站内元素有 20。
然后将 20 出栈。得到运算结果20。

经过一连串的接下来终于得到计算结果，对于前人的智慧结晶，我们应当永远都怀着敬畏和学习的心态。

现在了解了后缀表达式，那么现在还需要了解一下后缀表达式是怎么转化的来的。下面来了解一下中缀表达式。

中缀表达式：

我们把文章起始部分的数学运算表达式( 1 +（2 + 3）* 4 + ( 5 - 6 ) / 1 )叫做中缀表达式，因为所有的运算符号都处于两个数字的中间。

中缀表达式规则如下：

从左到用遍历中缀表达式的每个数字和符号，若是数字就输出，成为后缀表达式的一部分；若是符号，则判断其与栈顶符号的优先级，是右括号或优先级不低于不高于栈顶符号(乘除优先于加减)则栈顶元素一次出栈并输出，并将当前符号进站，一直到最终输出后缀表达式为止。

现在来使用中缀表达式的规则将篇头部分的运算表达式转换成后缀表达式：

首先初始化一个空栈，用来进行相关运算。同时记录输出的后缀表达式部分。
第一个是数字 1 ，输出到后缀表达式部分。这时候栈内元素为空，输出表达是部分为 1。
接下来是符号 + ，+ 入栈。这时候栈内元素为 + ，输出表达是部分为 1。
接下来是符号（，（入栈。这时候栈内元素为 + （，输出表达是部分为 1。
接下来是数字 2 ，输出到后缀表达式部分。这时候栈内元素为 + （，输出表达是部分为 1 2。
接下来是符号 + ，+ 入栈。这时候栈内元素为 + （ + ，输出表达是部分为 1 2。
接下来是数字 3 ，输出到后缀表达式部分。这时候栈内元素为 + （ + ，输出表达是部分为 1 2 3。
接下来是符号），发现是），所以将栈内元素出栈，直到与之匹配的（出栈为止。这时候栈内元素为 + ，输出表达是部分为 1 2 3 +。
接下来是符号 * ，* 入栈。这时候栈内元素为 + * ，输出表达是部分为 1 2 3 +。
接下来是数字 4 ，输出到后缀表达式部分。这时候栈内元素为 + * ，输出表达是部分为 1 2 3 + 4。
接下来是符号 + ，+ 优先级低于栈顶元素 * ，所以讲栈内元素依次出栈，然后 + 入栈。这时候栈内元素为 + ，输出表达是部分为 1 2 3 + 4 * +。
接下来是符号（，（入栈。这时候栈内元素为 + （，输出表达是部分为 1 2 3 + 4 * +。
接下来是数字 5 ，输出到后缀表达式部分。这时候栈内元素为 + （，输出表达是部分为 1 2 3 + 4 * + 5。
接下来是符号 - ，- 入栈。这时候栈内元素为 + （ - ，输出表达是部分为 1 2 3 + 4 * + 5。
接下来是数字 6 ，输出到后缀表达式部分。这时候栈内元素为 + （ - ，输出表达是部分为 1 2 3 + 4 * + 5 6。
接下来是符号），发现是），所以将栈内元素出栈，直到与之匹配的（出栈为止。这时候栈内元素为 + ，输出表达是部分为 1 2 3 + 4 * + 5 6 -。
接下来是符号 / ，/ 入栈。这时候栈内元素为 + / ，输出表达是部分为 1 2 3 + 4 * + 5 6 -。
接下来是数字 1 ，输出到后缀表达式部分。这时候栈内元素为 + / ，输出表达是部分为 1 2 3 + 4 * + 5 6 - 1。
此时运算表达式遍历完毕，讲栈内元素依次出栈。这时候栈内元素为空，输出表达是部分为 1 2 3 + 4 * + 5 6 - 1 / +。

又是一顿猛如虎的接下来操作，终于将中缀表达式转化成了后缀表达式。深吸一口气缓解一下。

我们发现在这两个表达式的规则中，栈都是一个很重要的元素，这是栈的应用之一。

总结

栈的应用还有很多，希望在未来的工作中我们能进行更多的挖掘。如果对于栈的知识还不清楚，可以查看今天第一篇文章。同时希望可以小手动一下给个关注，希望今后能够一起学习。

关注我的公众号，一起来学习更多的知识吧～