序言
最近在看一点关于计算机编程基础的内容,在讲到汇编被转为更底层的机器码的过程中忽然对二进制的一些内容感到很疑惑,一直以来对这块的内容只有在学校的时候有接(听)触(说)过,话不多说,带着几个问题,站在大佬们的基础上,做一个简单的解释和总结。
准备好纸和笔,有没明白的地方,可以手算一下,你会发现很多计算机先人们智慧的结晶~
计算机为什么要用二进制来运算
使用二进制的计算对实现计算机来说不是一个充分必要条件,理想条件下可以有N进制的cpu,但是考虑以下问题:
- 物理实现复杂度:如果用二进制的话门电路的导通与截止,电压的高压与低压,都可以完美的表示二进制的所有数字0和1,如果是10进制,实现0-9这10个稳定状态的电路和电压,是比较困难的,不过已经有人在研究3进制计算机了~
- 运算实现复杂度:对N进制的求和或者求积各有N(N+1)/2种,对于二进制来说就是2*3/2=3种,比如加法,分别是
0 + 0 = 0; 0 + 1 = 1; 0 + 1 = 10;如果换成10进制的话,就会有10*11/2 = 55种,这对于计算机的实现来说也是相当复杂的。 - 电路的0,1可以想象成没电和有电,这种条件下电路的稳定性是比较可靠的,如果化成10份,抗干扰能力急剧下降,会出现不合预期的干扰情况,因此鉴于机器的可靠性,二进制是最优的解。
- 最后就是逻辑判断非常方便,1是true 0是false,非常自然
当然有优点就一定有缺点,缺点就是二进制的书写是非常不方便的,可读性也很差,这也是很多语言为什么会需要汇编来做一个中间过程~,起码汇编的可读性比二进制强很多,另外基于汇编还可以做一些代码的优化~
综合而言,二进制天生符合计算机的脾气~
计算机怎么计算1-1的?
这是个展示人类先进思维的地方,首先,我们需要知道一点,二进制的计算过程没有减法,比如计算1-1 会被转化成 1+(-1),实现一个减法的过程不是不可以,而是对计算机的成本太大,代价也很大,尤其要考虑到减数,被减数,以及结果的正负,转换成加上一个负数,可以统一计算过程(都是加法),大大减小了计算的复杂性。
我们以8位的二进制数字来解释,伟大的计算机先人们为了解决正负数的问题,把一个二进制的首位定义为一个数字的正负,所以 1 的二进制原码是 0000 0001,-1的二进制原码是 1000 0001;当正真开始计算的时候,问题出现了:
| 十进制 | 二进制原码 | 计算结果 |
|---|---|---|
| 1 | 0000 0001 | |
| -1 | 1000 0001 | |
| 操作 | 加法 | 1000 0010 |
二进制原码:原码是指将最高位作为符号位(0表示正,1表示负),其它数字位代表数值本身的绝对值的数字表示方式。
what,惊人的发现结果是十进制的-2,这不是想要的结果,同时因为首位数字是符号位的原因,会导致2个0,0000 0000代表+0,1000 0000 代表-0,基于以上的问题,伟大的先人们发明了反码,反码:如果是正数,则表示方法和原码一样;如果是负数,符号位不变,其余各位取反,则得到这个数字的反码表示形式,有了反码,我们可以看看可以解决哪些问题:
| 十进制 | 二进制原码 | 二进制反码 | 计算结果 |
|---|---|---|---|
| 1 | 0000 0001 | 0000 0001 | |
| -1 | 1000 0001 | 1111 1110 | |
| 操作 | 加法 | 1111 1111 |
1111 1111 按照反码的格式,取反(原码取反再取反还是原码本身)过来就是10进制中的-0,因为 1000 0000 的反码就是 1111 1111,所以通过反码的形式,先人们完美的解决了 1 + (-1) = 0的问题,但是上面说到还有一个问题,+0 和 -0 这个现象依然存在,就像坏了一锅汤的老鼠一样,伟大的先人们的智慧当然不允许这种情况的存在,于是乎,有人创造了 补码,补码:如果是正数,则表示方法和原码一样;如果是负数,则将数字的反码加上1(相当于将原码数值位取反然后在最低位加1
有了补码之后,1的补码是:0000 0001, -1的补码是 1111 1111 当我们去相加的时候:
| 十进制 | 二进制原码 | 二进制反码 | 二进制反码 | 计算结果 |
|---|---|---|---|---|
| 1 | 0000 0001 | 0000 0001 | 0000 0001 | |
| -1 | 1000 0001 | 1111 1110 | 1111 1111 | |
| 操作 | 加法 | (1)0000 0000 |
在反码的基础上,补了一位之后,我们发现结果正是我们想要的,而且不会有-0的出现了,但是有得必有失,我们丢了-0,但是我们获取了-128,为啥?-0 的补码是 1000 0000 所以,先人前辈们把这个补码定义成了当前补码范围内可以表示的最小的负整数,8位的二进制就是-128,这也是为啥8位二进制表示的数字范围是[-128, 127]的原因,-0 丢了,但是加了一个-128,现在我们通过补码的形式把这个坏老鼠成功的剔除掉了,一切的计算看起来都是那么的完美~
现在我们完整的走一次计算过程,以1-2=-1来实现:
| 十进制 | 二进制补码 | 计算结果 |
|---|---|---|
| 1 | 0000 0001 | |
| -2 | 1111 1110 | |
| 操作 | 加法 | 1111 1111 |
结果是负数,所以想知道它具体是多少需要通过补码来查看,所以 1111 1111的补码是 1000 0001 就是十进制的-1
为什么对负数结果要求补码? 其实我们运算的过程就是用的补码,那么理论上应该是反补码才能拿到实际的数据,but but 这里为什么正向求补码了?这就是二进制非常神奇的地方,一个二进制的原码的补码的补码就是 -----> 这个原码本身(就好像一个原码的反码的反码还是原码一样自然),正数因为补码永远是自己,所以肯定是成立的,对于负数,验证如下:
1000 0001 求补 1111 1111
1111 1111 求补 1000 0001
所以,对于计算机来说运算之前求一次补码,运算之后再求一次补码,就可以拿到正确的结果拉,一切都是那么的自然。。
不好理解?放2个图,让你一眼就看明白
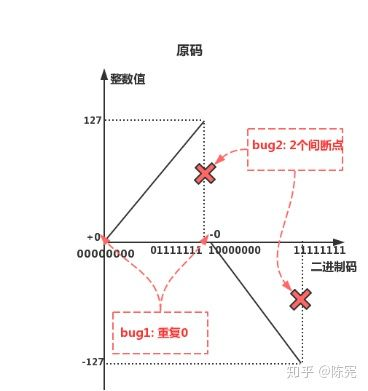
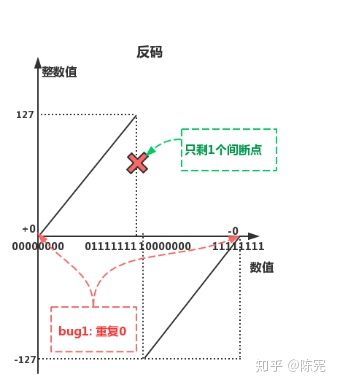
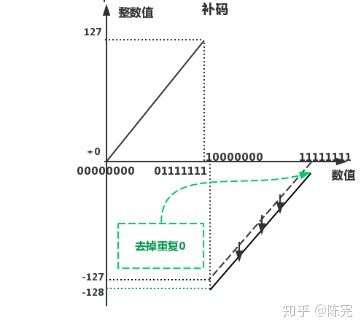
如果看不明白的话,请查看原作者的解释,在这里
现在我们都学到了,原来正真在最底层吭哧吭哧进行运算的,都是二进制补码~
为什么会溢出?
理论上N位二进制所能表达的数字一定是有限的,比如8位二进制的范围就是[-128, 127],当计算到127的时候,+1 就会"跳"到-128,就像一个圆圈一样,一切都回到了原点重新开始,只是这个临界点不是“0”而是“127”和“-128”,所以,溢出是一定会出现的,当计算结果超出当前range范围,就会产生溢出的行为,理解这个行为,我们要先理解“模”这个概念;
假如给一个钟表,因为钟表的范围一共就是12个格子,所以“12”就是它的“模”,超过12就会重新计算,这种现象,就是“溢出”,在看下面的例子:假如现在时针在2点的位置,如果我想要他变为6点,有几种办法,理论上有N种,我可以不停的旋转然后再回来,我们讨论最基本的,其实是2种,正向走过4个格子,到6,这就是 2 + 4 = 6;还可以反向走 8 个格子,[2>1>12>11>10>9>8>7>6] ,会发现一个绝妙的点:4+8=12,同时,4和8就是对于“模”12的一对补数,在钟表上我们可以看出来2-8==2+4 往后退8个就等于往前走4个,也就是说,在“模”运算中,x-y==x+y的补数,回到二进制,二进制的计算和钟表的计算是非常像的,8位二进制的“模”就是256,从[0-127]以及[-1,-128],各有128位数字,到达临界点的时候就会break到下一个原始的点,比如从-128 再走就回到 +127,从+127再走就到了-128,

这些在计算上的表现就是低位进位导致高位溢出,所以符号位就是不断的被“取反”,丢掉的高位,就好比是时钟走完了一圈,进入下一圈后上一圈就没了,同样,补码的设计,就实现了减法变成加法的运算,比如我们在计算127+1,补码运算得到的结果是-128,二进制的 1000 0000,那么实际的值就是结果的补码,对-128的补码,就是用“模”-|-128|(注意:这里的补数计算,一定是绝对值,正数就是正数本身,负数,就是绝对值),就等于256-128 = 128,所以127 + 1 = 128
然后,我们用一段c++代码来看下这个答案:
#include <stdio.h>
int main(void)
{
char a, b;
char c;
a = 127;
b = 1;
c = a + b;
printf("c=%d", c);
return 0;
}
输出是-128,这是因为,8位我们知道最大能表示的正数是127,128当然无法表示了,因此会从127 跳到下一位,发生一次符号的反转,就是-128,这个溢出导致的结果会引起无法预期的bug,如果我们把c的长度换位16位的二进制:
#include <stdio.h>
int main(void)
{
char a, b;
short c;
a = 127;
b = 1;
c = a + b;
printf("c=%d", c);
return 0;
}
输出就是 128~
所以在有位数限制的语言中,一定要注意计算溢出的问题~
二进制的乘除
二进制乘法
从上面的描述我们知道了二进制只有加法,没有减法,那么有的小伙伴肯定会有疑问了,减法都没有,那乘法怎么办?我们看看计算机通过二进制是怎么解决乘法问题的:
从我们已知的十进制说起,假设我有一个数字900.000,我现在想对900做乘法,算900*10=? 从我们接触小数点的时候,老师应该都说过,遇到*10的情况,我们就数一下乘数有几个0,1后面几个0就把小数点往右边移动几位,所以这里我们把小数点往后移动一位,结果就是9000.00,现在我们忽略小数点,和后面的0,发现乘以10的过程,实际就是把900全部左移了一位,最后补了一个0,对吧,也就是每次的左移1位代表对被乘数乘以10,右移一位就表示除以10~
回到二进制的世界,理论都是一样的,只是逢十变成了逢二而已,但是巧就巧在,10进制中我们的乘数可能不是10的整数次幂,比如*5,*3,但是二进制情况下,所有的数字都是2的整数次幂,比如我有一个二进制的数据 0000 0001 乘以 10 (注意,10是十进制的2),那就把被乘数所有的数字全部往左移动一位,就代表乘以2没问题,所以结果就是0000 0010 高位舍去,低位补0~,所有的二进制的复杂乘法都是通过这个方式(移位+加法)来实现的,我们看个比较复杂的例子:
1111 * 111
首先,乘数 111 分别表示是2º、2¹、2²,什么意思,就好比十进制的9 * 110 可以分解为 9 * 10¹ + 9 * 10²,对应就是9向左移1位得到90 + 9向左移2位得到900 = 990,同理,对于二进制来说 0就是不移位,那就是1111,1表示左移1位,就是11110 ,2就是左移2位,就是111100,然后计算二进制加法
加法计算:
| 0000 1111 | |
| 0001 1110 | |
| 0011 1100 | |
| 加法 | 0110 1001 |
得到结果 0110 1001 转化为10进制就是:
15 * 5 = 105
完美,所以可以看到整个计算过程都是通过移位+加法来解决问题的,所以,现在你应该知道为什么面试中问你计算2³最快的方式是2<<2了吗?
二进制除法
除法的运算相对复杂和耗时一些,还是以10进制的计算过程为例:
计算 19 / 3 = ?
因为我没有乘除,只能用加法来解决问题,但是我知道除数和被除数,那么,我先用一个除数和被除数比,发现 3 < 19,那么给我的除数再加上一个除数,一直继续,整体过程就是
3 < 19 商 + 1 当前中间计算结果 3
6 < 19 商 + 1 当前中间计算结果 6
9 < 19 商 + 1 当前中间计算结果 9
12 < 19 商 + 1 当前中间计算结果 12
15 < 19 商 + 1 当前中间计算结果 15
18 < 19 商 + 1 当前中间计算结果 18
21 > 19 停止 此时商从0变为 6 余数为 19 - 18(中间数)= 1
计算得出余数为1 商为6 返回计算结果~
其实就是不停的累加除数的过程,一直到找到第一次累加之和超过被除数的上一次为止~,剩下的就是余数
当然,换做二进制,流程是一样的,只是都用二进制去计算~,我就不细说了,除法还是比较麻烦的,需要用到至少4个寄存器,存放除数,被除数,中间数,以及商,最后的余数就直接用被除数-中间数就可以了~
所以,尽量能用位移,不用加减,能用加减不用乘除,能用乘法,不用除法~
总结
- 二进制都是以补码的方式在底层做运算;
- 有限范围内的计算溢出会导致不可预期的结果,
- 8位的-128是先人们智慧的结晶,当然还有16位的-xx,以及32位的-xx等等
- 计算机的世界,没有减乘除,只有加法~
本文有一些内容是总结和引用,有一些是笔者自己的理解,如有错误,请海涵并指出~
不针对浮点数的运算,因为运算方式完全不同于整数
二进制非常简单,但是又非常的绝妙,如果能仔细体会的话
如果以上内容对你有点帮助,希望可以给个赞
后续可能会再总结一下为何0.1+0.2!=0.3的问题~