线性代数基础

标量

定义

一个单独的数

表示

斜体小写字母： $a$
希腊字母： $\alpha$

向量

定义

具有大小（magnitude）和方向的量

表示

粗体小写字母： $\boldsymbol{x}$
粗体希腊字母： $X$
箭头表示： $\vec{X}$
元素： $x_{i}$

模

$|\overrightarrow{\mathbf{a}}|=\sqrt{\mathbf{x}_{1}^{2}+\mathbf{x}_{2}^{2}+\cdots+\mathbf{x}_{\mathrm{N}}^{2}}$

范数

在一个 $n$ 维线性空间 $V$ 中，若对于任意向量 $\mathrm{x} \in \mathrm{V}$ ,均有非负实数 $\|\mathbf{X}\|$ ,并且其满足下列三个条件:

（非负性）: $\|\mathrm{x}\| \geq 0$ 当且仅当 $\mathrm{x}=0$ 时 $\|x\|=0$
（齐次性）: $\|\lambda \mathrm{x}\|=|\lambda| \cdot\|x\|$
（三角不等式）: $\|\mathrm{x}+\mathrm{y}\| \leq\|x\|+\|y\| ; x, y \in V$

则称 $\|X\|$ 是向量 $x$ 的向量范数。

1-范数

$\|\overrightarrow{\mathbf{x}}\|_{1}=\sum\left|\mathbf{x}_{\mathbf{i}}\right|$ $\|x\|_{1}=\sum_{i=1}^{n}\left|x_{i}\right|$

2-范数（欧式范数）

$\|\overrightarrow{\mathbf{x}}\|_{2}=\sqrt{\mathbf{x}_{1}^{2}+\mathbf{x}_{2}^{2}+\cdots+\mathbf{x}_{\mathrm{N}}^{2}}$ $\|x\|_{2}=\sqrt{\sum_{i=1}^{n} x_{i}^{2}}$

∞-范数（无穷范数）

$\|\overrightarrow{\mathbf{x}}\|_{\infty}=\max \left|\mathbf{x}_{\mathbf{i}}\right|$ $\|x\|_{n}=\max \left|x_{i}\right|$

运算

加法

$\left[\begin{array}{c}{x_{1}} \\ {\vdots} \\ {x_{n}}\end{array}\right]+\left[\begin{array}{c}{y_{1}} \\ {\vdots} \\ {y_{n}}\end{array}\right]=\left[\begin{array}{c}{x_{1}+y_{1}} \\ {\vdots} \\ {x_{n}+y_{n}}\end{array}\right]$

$\left[\begin{array}{llll}{x_{1}} & {\cdots} & {x_{n}}\end{array}\right]+\left[\begin{array}{lll}{y_{1}} & {\cdots} & {y_{n}}\end{array}\right]=\left[\begin{array}{llll}{x_{1}+y_{1}} & {\cdots} & {x_{1}+y_{n}}\end{array}\right]$

数乘

$\boldsymbol{c} \cdot\left[\begin{array}{c}{\boldsymbol{x}_{1}} \\ {\vdots} \\ {\boldsymbol{x}_{\boldsymbol{n}}}\end{array}\right]=\left[\begin{array}{c}{\boldsymbol{c} \cdot \boldsymbol{x}_{1}} \\ {\vdots} \\ {\boldsymbol{c} \cdot \boldsymbol{x}_{\boldsymbol{n}}}\end{array}\right]$

$c \cdot\left[\begin{array}{lll}{x_{1}} & {\cdots} & {x_{n}}\end{array}\right]=\left[\begin{array}{lll}{c \cdot x_{1}} & {\cdots} & {c \cdot x_{n}}\end{array}\right]$

点积

$\vec{a}=\left[a_{1,} a_{2} \cdots a_{n}\right]$ $\vec{b}=\left[b_{1}, b_{2}, \cdots, b_{n}\right]$

定义

$\vec{a} \cdot \vec{b}=\sum_{i=1}^{n} a_{i} b_{i}=a_{1} b_{1}+a_{2} b_{2}+\cdots+a_{n} b_{n}$

$\vec{a} \cdot \vec{b}=\left|\vec{a} \cdot \vec{b}^{\mathrm{T}}\right|$

几何定义

$\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}=|\mathbf{a}||\mathbf{b}| \cos \theta$

高维

$\langle\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}\rangle=\sum_{i=1}^{\mathbf{n}} \mathbf{a}_{\mathbf{i}} \mathbf{b}_{\mathbf{i}}$

矩阵

机器学习基础公式

$y=f(x)=x w^{T}+b$

定义

二维数组

表示

$\left[\begin{array}{ccc}{a_{11}} & {\cdots} & {a_{1 N}} \\ {\vdots} & {\ddots} & {\vdots} \\ {a_{M 1}} & {\cdots} & {a_{M N}}\end{array}\right]$

大写字母： $\mathrm{A}$
m×n 矩阵 A： $\mathrm{A}_{m n}$

运算

加法

对应元素相加

$A+B=C \Rightarrow a_{i j}+b_{i j}=c_{i j}$

$\left[\begin{array}{ccc}{a_{11}} & {\cdots} & {a_{1 N}} \\ {\vdots} & {\ddots} & {\vdots} \\ {a_{M 1}} & {\cdots} & {a_{M N}}\end{array}\right]+\left[\begin{array}{ccc}{b_{11}} & {\cdots} & {b_{1 N}} \\ {\vdots} & {\ddots} & {\vdots} \\ {b_{M 1}} & {\cdots} & {b_{M N}}\end{array}\right]=\left[\begin{array}{ccc}{a_{11}+b_{11}} & {\cdots} & {a_{1 N}+b_{1 N}} \\ {\vdots} & {\ddots} & {\vdots} \\ {a_{M 1}+b_{M 1}} & {\cdots} & {a_{M N}+b_{M N}}\end{array}\right]$

基本性质

交换率： $(\boldsymbol{A}+\boldsymbol{B})+\boldsymbol{C}=\boldsymbol{A}+(\boldsymbol{B}+\boldsymbol{C})$
结合率： $\boldsymbol{A}+\boldsymbol{B}=\boldsymbol{B}+\boldsymbol{A}$

乘法

$\mathrm{A}_{m n}$

$\mathrm{B}_{n p}$

$\boldsymbol{A}$ 的列数与 $\boldsymbol{B}$ 的行数相等

$\mathrm{C}_{m p}$

$C=A B$

$C_{i j}=\sum_{k} A_{i k} B_{k j}$

$A=\left[\begin{array}{ccc}{a_{11}} & {\cdots} & {a_{1 N}} \\ {\vdots} & {\ddots} & {\vdots} \\ {a_{M 1}} & {\cdots} & {a_{M N}}\end{array}\right]$

$B=\left[\begin{array}{ccc}{b_{11}} & {\cdots} & {b_{1 P}} \\ {\vdots} & {\ddots} & {\vdots} \\ {b_{N 1}} & {\cdots} & {b_{N P}}\end{array}\right]$

$C=\left[\begin{array}{ccc}{c_{11}} & {\cdots} & {c_{1 P}} \\ {\vdots} & {\ddots} & {\vdots} \\ {c_{M 1}} & {\cdots} & {c_{M P}}\end{array}\right]$

$c_{i j}=a_{i 1} b_{1 j}+\cdots+a_{i m} b_{m j}=\sum_{k=1}^{m} a_{i k} b_{k j}$

矩阵乘法一般不满足交换律

转置

$\boldsymbol{A}^{\top}$

定义

$\left(\boldsymbol{A}^{\top}\right)_{i, j}=A_{j, i}$

特殊矩阵

单位矩阵

$\left[\begin{array}{lll}{1} & {0} & {0} \\ {0} & {1} & {0} \\ {0} & {0} & {1}\end{array}\right]$

零矩阵 / 全0矩阵

$\left[\begin{array}{lll}{0} & {0} & {0} \\ {0} & {0} & {0} \\ {0} & {0} & {0}\end{array}\right]$

全1矩阵

$\left[\begin{array}{lll}{1} & {1} & {1} \\ {1} & {1} & {1} \\ {1} & {1} & {1}\end{array}\right]$

对角矩阵

$\left[\begin{array}{ccc}{a_{11}} & {0} & {0} \\ {0} & {a_{22}} & {0} \\ {0} & {0} & {a_{33}}\end{array}\right]$

上三角矩阵

$\left[\begin{array}{ccc}{a_{11}} & {a_{21}} & {a_{31}} \\ {0} & {a_{22}} & {a_{32}} \\ {0} & {0} & {a_{33}}\end{array}\right]$

下三角矩阵

$\left[\begin{array}{lll}{a_{11}} & {0} & {0} \\ {a_{12}} & {a_{22}} & {0} \\ {a_{13}} & {a_{23}} & {a_{33}}\end{array}\right]$

基本性质

乘法结合律： $\left(\boldsymbol{A B}\right)\boldsymbol{C}=\boldsymbol{A}\left(\boldsymbol{B C}\right)$
乘法左分配律： $\left(\boldsymbol{A+B}\right)\boldsymbol{C}=\boldsymbol{A C}+\boldsymbol{BC}$
乘法右分配律： $\boldsymbol{C}\left(\boldsymbol{A+B}\right)=\boldsymbol{C A}+\boldsymbol{CB}$
对数乘的结合性： $k\left(\boldsymbol{A B}\right)=\left(k\boldsymbol{A}\right)\boldsymbol{B}=\boldsymbol{A}\left(k\boldsymbol{B}\right)$
转置 $\left(\boldsymbol{A B}\right)^{\top}=\boldsymbol{B}^{\top}\boldsymbol{A}^{\top}$

线性相关

向量空间的一组元素中，若没有向量可用有限个其他向量的线性组合所表示，则称为 线性无关 或 线性独立，反之称为 线性相关(linearly dependent)。

结论

含有零向量的向量组一定线性相关
单位向量组线性无关

秩

向量组的秩

一个向量组 $A$ 的秩是 $A$ 的线性无关的向量的个数

矩阵的秩

如果把一个向量组看成一个矩阵，则向量组的秩就是矩阵的秩

范数

在一个 $n*m$ 维线性空间 $V$ 中，若对于任意矩阵 $\mathrm{A} \in \mathrm{V}$ ,均有非负实数 $\|\mathbf{A}\|$ ,并且其满足下列四个条件:

（非负性）: $\|A\| \geq 0$ 当且仅当 $A=0$ 时 $\|A\|=0$
（齐次性）: $\|\lambda \mathrm{A}\|=|\lambda| \bullet\|A\|$
（三角不等式）: $\|\mathrm{A}+\mathrm{B}\| \leq\|\mathrm{A}\|+\|\mathrm{B}\| ; \mathrm{A}, \mathrm{B} \in V$
（相容性）: $\|A B\| \leq\|A\| \bullet\|B\| ; A, B \in V$

则称 $\|A\|$ 是向量 $A$ 的向量范数。

1-范数（列范数）

$\|A\|_{1}=\max _{1 \leq j \leq n} \sum_{i=1}^{n}\left|a_{i j}\right|$

∞-范数（行范数）

$\|A\|_{\infty}=\max _{1 \leq i \leq n} \sum_{j=1}^{n}\left|a_{i j}\right|$

2-范数

$\|A\|_{2}=\sqrt{\lambda_{\max }\left(A^{T} A\right)}$

$\lambda_{\max }\left(A^{T} A\right)$ 为 $A^{T} A$ 的特征值的绝对值的最大值

范数作用

计算向量/矩阵相似程度
计算向量距离

迹

在线性代数中，一个 $n \times n$ 的矩阵的迹（或迹数），是指的 主对角线（从左上方至右下方的对角线）上各个元素的总和，一般记作或 $\operatorname{tr}(\mathbf{A})$ ：

$\operatorname{tr}(\mathbf{A})=\mathbf{A}_{1,1}+\mathbf{A}_{2,2}+\cdots+\mathbf{A}_{n, n}$

一个矩阵的迹是其 特征值 的总和（按代数重数计算）。

线性变换

n 个向量 $x_{1}, x_{2}, \cdots, x_{n}$ 与 m 个向量 $\boldsymbol{y}_{1}, \boldsymbol{y}_{2}, \cdots, \boldsymbol{y}_{m}$ 之间的关系

$\left\{\begin{aligned} y_{1} &=a_{11} x_{1}+a_{12} x_{2}+\cdots+a_{1 n} x_{n} \\ y_{2} &=a_{21} x_{1}+a_{22} x_{2}+\cdots+a_{2 n} x_{n} \\ & \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\ y_{m} &=a_{m 1} x_{1}+a_{m 2} x_{2}+\cdots+a_{m n} x_{n} \end{aligned}\right.$

表示从一个变量 $x_{1}, x_{2}, \cdots, x_{n}$ 到变量 $y_{1}, y_{2}, \cdots, y_{m}$ 的线性变换。

其中

$a_{i j}$ 为常数
$\boldsymbol{n} \neq \boldsymbol{m}$

$A=\left(\begin{array}{cccc}{a_{11}} & {a_{12}} & {\cdots} & {a_{1 n}} \\ {a_{21}} & {a_{22}} & {\cdots} & {a_{2 n}} \\ {\cdots} & {\cdots} & {\cdots} & {\cdots} \\ {a_{m 1}} & {a_{m 1}} & {\cdots} & {a_{m n}}\end{array}\right)$

系数矩阵

称之为 线性变换 的矩阵

线性变换 与矩阵是唯一确定的。

特征值与特征向量

设 $A$ 为 $n$ 阶矩阵，若存在常数 $\lambda$ 及 $n$ 维非零向量 $x$ ，使得

$A x=\lambda x(x \neq 0)$

则称 $\lambda$ 是矩阵 $A$ 的 特征值， $x$ 是 $A$ 对就特征值 $\lambda$ 的 特征向量。

$(A-\lambda I) x=0$ $|A-\lambda I|=0$

$\left|\begin{array}{cccc}{a_{11}-\lambda} & {a_{12}} & {\cdots} & {a_{1 n}} \\ {a_{21}} & {a_{22}-\lambda} & {\cdots} & {a_{2 n}} \\ {\cdots} & {\cdots} & {\cdots} & {\cdots} \\ {a_{n 1}} & {a_{n 2}} & {\cdots} & {a_{m n}-\lambda}\end{array}\right|=0$

称为矩阵 $A$ 的特征方程

应用

主成分分析
流行学习
LDA

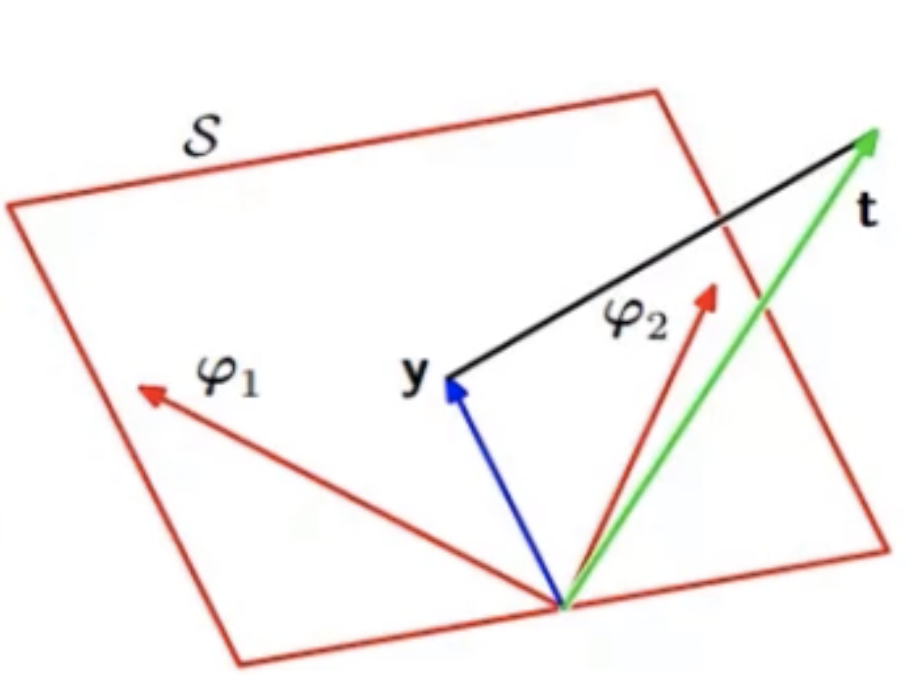
正交投影

二次型

n 个变量 $x_{1}, x_{2}, \cdots, x_{n}$ 的二次齐次多项式

$\begin{aligned} f\left(x_{1}, x_{2}, \cdots, x_{n}\right) &=a_{11} x_{1}^{2}+a_{12} x_{1} x_{2}+\cdots+a_{1 n} x_{1} x_{n} \\ &+a_{21} x_{2} x_{1}+a_{22} x_{2}^{2}+\cdots+a_{2 n} x_{2} x_{n} \\ &+\cdots \\ &+a_{n 1} x_{n} x_{1}+a_{n 2} x_{n} x_{2}+\cdots+a_{n n} x_{n}^{2} \end{aligned}$

其中 $a_{i j}=a_{j i}, 1 \leq i, j \leq n$

令

$A=\left(\begin{array}{cccc}{a_{11}} & {a_{12}} & {\cdots} & {a_{1 n}} \\ {a_{21}} & {a_{22}} & {\cdots} & {a_{2 n}} \\ {\vdots} & {\vdots} & {} & {\vdots} \\ {a_{n 1}} & {a_{n 2}} & {\cdots} & {a_{n n}}\end{array}\right), \quad X=\left(\begin{array}{c}{x_{1}} \\ {x_{2}} \\ {\vdots} \\ {x_{n}}\end{array}\right)$

则多项式可写为：

$f\left(x_{1}, x_{2}, \cdots, x_{n}\right)=X^{T} A X$

该多项式是 $n$ 元二次型，简称 二次型 该多项式也为二次型的矩阵形式

二次型经过变换，可以写成平方和形式

$\mathrm{d}_{1} y_{1}^{2}+\mathrm{d}_{2} y_{2}^{2}+\cdots+\mathrm{d}_{n} y_{n}^{2}$

称为多项式一个标准型。

[注]

任一二次型的标准型是存在的。

可应用配方法得到二次型的标准型。

矩阵分解

QR分解

设非奇异矩阵 $A \in R^{n \times n}$ ，则一定存在正交矩阵 $Q$ ,上三角矩阵 $R$ ,使

$A=Q R$

且当 $R$ 的主对角元素均为正数时，该分解式是唯一的。

[注]: 正交矩阵是 $\mathrm{QQ}^{\top}=\mathrm{E}$

SVD 奇异值分解

设 $A$ 是秩为 $r(r>0)$ 的 $m \times n$ 实矩阵，则存在 $m$ 阶正交矩阵 $U$ 与 $n$ 阶正交矩阵 $V$ ，

使得

$\boldsymbol{U}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{V}=\left[\begin{array}{cc}{\Sigma} & {\boldsymbol{O}} \\ {\boldsymbol{O}} & {\boldsymbol{O}}\end{array}\right]=S$

其中 $\Sigma=\operatorname{diag}\left(\sigma_{1}, \sigma_{2}, \cdots, \sigma_{r}\right) \quad(i=1,2, \cdots, r)$ $\sigma_{1} \geq \cdots \geq \sigma_{r}>0$ 为矩阵A的全部奇异值

线性代数基础

标量

定义

表示

向量

定义

表示

分类

行向量

列向量

模

范数

1-范数

2-范数（欧式范数）

∞-范数（无穷范数）

运算

加法

数乘

点积

定义

几何定义

高维

矩阵

定义

表示

运算

加法

基本性质

乘法

转置

定义

特殊矩阵

单位矩阵

零矩阵 / 全0矩阵

全1矩阵

对角矩阵

上三角矩阵

下三角矩阵

基本性质

线性相关

结论

秩

向量组的秩

矩阵的秩

范数

1-范数（列范数）

∞-范数（行范数）

2-范数

范数作用

迹

线性变换

特征值与特征向量

应用

正交投影

二次型

矩阵分解

QR分解

SVD 奇异值分解