上一节讲到了冒泡排序、插入排序和选择排序，这次进阶讲归并排序和快速排序。
一、归并排序（Merge Sort）
归并排序其实从字面上就能知道是什么意思，先讲数组切分两半，然后对剩余数组继续切割，直到不可再分割的时候两两比较排序，一块一块的合并成一个数组，这样就变成有序了。如同所示：
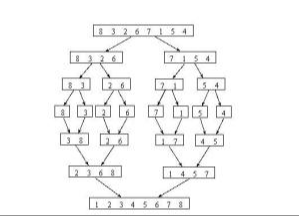
归并排序使用的就是分治思想。分治，顾名思义，就是分而治之，将一个大问题分解成小的子问题来解决。小的子问题解决了，大问题也就解决了。从上面对归并排序的描述里，它的实现方法有点像之前你文章里说到的递归。一般来说，分治都可以用递归来实现。分治是一种解决问题的处理思想，递归是一种编程技巧。其实递归和分治两者并不冲突，分治这个思想在算法会有很多地方用到。下面就来看看如何用递归来实现归并排序。
写一个递归代码首先是分析得出一个递推公式，然后找到一个终止条件，最后讲递推公式翻译成代码。所以成归并排序的定义我们可以马上的得出一个地推公式：
mergeSort(start, end) = merge(mergeSort(start, center), mergeSort(center + 1, end))
结束条件是起始下标大于等于结尾下标：
start >= end这个地推公式的含义是这样的，mergeSort表示的是一个排序方法，对起始下标和结尾下标之间的数据进行排序。等号右边的merge表示的是一个合并函数，将两个数组合并在一起。这里是将一个数组分成两份，如果这两份已经是有序了那么就可以很容易的合成一个有序数组。下面我们就将这个公式转换成代码来看看：
/**
* @param {Array} arr 要排序的数组
* @param {number} first 当前数组的第一个下标
* @param {number} last 当前数组的最后一个下标
* @description 归并排序的递归方法
* */
function mergeSort(arr, first, last) {
if (first >= last) return;
let center = Math.floor((first + last) / 2);
mergeSort(arr, first, center);
mergeSort(arr, center + 1, last);
merge(arr, first, center, last)
}上面所说，merge函数只是一个合并函数，将两组数组合并成一个有序数组，那么这个合并操作是如何实现的呢？
首先我们要弄一个临时数组temp，长度是end到start。新建两个下标i和j分别指向arr[start...center]和arr[center+1...end]的第一个元素，然后利用双指针的方法来进行遍历比较，如果第一个数组下标i所对应的元素比第二个数组下标j所对应的元素小，则i所对应的元素压入temp数组中，反之则j所对应的元素压入temp数组中。最后直到某个数组已经遍历完成的时候，另一个数组剩余的元素将全部压入到temp数组中。代码如下：
/**
* @param {Array} arr 要合并的数组
* @param {number} first 当前数组第一个下标
* @param {number} center 当前数组的中间下标
* @param {number} last 当前数组的最后一个下标
* @description 归并排序合并方法
* */
function merge(arr, first, center, last) {
let i = first, j = center+ 1, k = 0;
let temp = new Array(last-first);
while (i <= center && j <= last) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++]
}
else {
temp[k++] = arr[j++]
}
}
let start = i, end = center;
if (j <= last) {
start = j;
end = last
}
while (start <= end) {
temp[k++] = arr[start++]
}
for (let i = 0; i <= last - first; i++) {
arr[first+i] = temp[i]
}
}二、归并排序的性能分析
现在我们按照上一篇文章里分析排序算法性能所用到的稳定性分析和复杂度分析，来分析一下归并排序。
1、稳定性分析
首先是稳定性分析。在合并的过程中，如果两个数组之间是有相同的元素的，在上面的merge代码实例里，我们在第五行的判断语句里，将第一个数组里相同的元素都优先压入temp中，这样保证了数据的顺序，所以这个是稳定性算法。
2、时间复杂度分析
那么归并排序的时间复杂度是多少呢？由于这个归并排序是由递归来实现的，所以我们来分析一下这个递归的时间复杂度是多少。首先递归它的使用场景是将问题不断的分解，直到问题不能分解的时候解决子问题，然后合并结果。假设一个问题a分解成问题b和问题c，那么地推关系式如下：
T(a) = T(b) + T(c) + K这里的K表示的是子问题合并成总问题所需要的时间。从这里我们可以知道，不仅递归求解的问题可以写成递推公式，递归代码的时间复杂度也可以写成地推公式。利用公式，我们可以分析一下归并排序的时间复杂度。我们假设对 n 个元素进行归并排序需要的时间是 T(n)，那分解成两个子数组排序的时间都是 T(n/2)。我们知道，merge() 函数合并两个有序子数组的时间复杂度是 O(n)。所以，套用前面的公式，归并排序的时间复杂度的计算公式就是：
T(1) = C； n=1 时，只需要常量级的执行时间，所以表示为 C。
T(n) = 2*T(n/2) + n； n>1然后上面的公式可以进一步推导得：
T(n) = 2*T(n/2) + n
= 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
= 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
= 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n
......
= 2^k * T(n/2^k) + k * n
......所以得到等式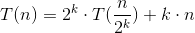
，这里我们令n=1，可得
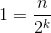，也就是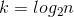
。当我们把k的值重新带入等式中：
T(n) = n*T(1) + nlogn
= nc + nlogn这里用大O标记法来表示的话，T(n) = O(nlogn)，所以归并排序的时间复杂度是O(nlogn)。
3、空间复杂度分析
由于归并排序每次执行合并操作的时候都需要申请一个额外的空间，所以归并排序不是原地排序算法。在上面的代码里归并排序执行了n次合并，所以申请了n个额外的存储空间，因此空间复杂度是O(n)。而在上一篇文章里讲到原地排序算法是指空间复杂度为O(1)的算法，由于要牺牲额外的空间，所以对比快速排序，归并排序比它差了点。
三、快速排序（Quick Sort）
快排的思想是这样的：如果要排序数组中下标从 p 到 r 之间的一组数据，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点）。我们遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot 的。
举个例子，比如我们有一组数据：20，40，50，10，60。按照上面的说法首先p指针指的是20这个元素，r指针指的是60这个元素，pivot指针我们假设指向20。
首先r指针向后遍历寻找比pivot指针小的元素，这时r指针找到了10，所以将r指针的值与p指针的值互换得：10，40，50，10，60。
此时r指针暂停遍历，轮到p指针开始向后遍历，寻找比pivot指针还大的元素，这时p指针找到了40，所以将p指针的值与r指针的值互换得：10，40，50，40，60。
然后下一步p指针暂停遍历，r指针开始遍历，重复上面操作，直到p指针和r指针重合的时候重合指向的元素的值变为pivot指针的值，得：10，20，50，40，60。这个时候pivot指针前面的元素都比它小，后面的元素都比它大，然后程序继续重复执行上面的操作，就可以得到一个有序的数组。
通过这个操作我们可以得到一个递推公式：
quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1, r)
终止条件：
p >= r然后根据这个公式可以得出一个代码：
/**
* @param {Array} arr 要排序的数组
* @param {number} start 当前数组的第一个下标
* @param {number} end 当前数组的最后一个下标
* @description 快速排序的递归方法
* */
function quickSort(arr, start, end) {
if (start >= end) return false
let pivot = partition(arr, start, end)
quickSort(arr, start, pivot - 1)
quickSort(arr, pivot + 1, end)
}这里的partition函数指的是一个分区函数，返回一个分区指针。如果我们不考虑空间消耗的话，partition() 分区函数可以写得非常简单。我们申请两个临时数组 X 和 Y，遍历 A[p…r]，将小于 pivot 的元素都拷贝到临时数组 X，将大于 pivot 的元素都拷贝到临时数组 Y，最后再将数组 X 和数组 Y 中数据顺序拷贝到 A[p…r]。但是，如果按照这种思路实现的话，partition() 函数就需要很多额外的内存空间，所以快排就不是原地排序算法了。如果我们希望快排是原地排序算法，那它的空间复杂度得是 O(1)，那 partition() 分区函数就不能占用太多额外的内存空间，我们就需要在 A[p…r] 的原地完成分区操作。
那如何实现这个partition函数呢，代码如下：
/**
* @param {Array} arr 要合并的数组
* @param {number} start 当前数组第一个下标
* @param {number} end 当前数组的最后一个下标
* @description 快速排序合并方法
* */
function partition(arr, start, end) {
let pivot = arr[end]
let i = start
for (let j = start; j <= end - 1; j++) {
if (arr[j] < pivot) {
let temp = arr[i]
arr[i] = arr[j]
arr[j] = temp
i = i + 1
}
}
let temp = arr[i]
arr[i] = arr[end]
arr[end] = temp
return i
}
// 或者下面这种分类方法
function partition(arr, left, right) {
let i = left, j = right, temp = arr[left]
while (i !== j) {
while (i < j && arr[j] >= temp) {
j--
}
if (j > i) {
arr[i] = arr[j]
}
while (i < j && arr[i] <= temp) {
i++
}
if (i < j) {
arr[j] = arr[i]
}
}
arr[i] = temp;
return i
}因为分区的过程涉及交换操作，如果数组中有两个相同的元素，比如序列 6，8，7，6，3，5，9，4，在经过第一次分区操作之后，两个 6 的相对先后顺序就会改变。所以，快速排序并不是一个稳定的排序算法。
到此，我们发现：快排和归并用的都是分治思想，递推公式和递归代码也非常相似，那它们的区别在哪里呢？
归并排序的处理过程是由下到上的，先处理子问题，然后再合并。而快排正好相反，它的处理过程是由上到下的，先分区，然后再处理子问题。归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法，但是它是非原地排序算法。我们前面讲过，归并之所以是非原地排序算法，主要原因是合并函数无法在原地执行。快速排序通过设计巧妙的原地分区函数，可以实现原地排序，解决了归并排序占用太多内存的问题。
四、快速排序的性能分析
1、稳定性分析
由于快速排序需要分区，在分区的过程中可能会导致等值相邻元素的先后顺序发生改变，所以快排并不是稳定性排序算法。
2、时间复杂度分析
快排也是用递归来实现的。对于递归代码的时间复杂度，我前面总结的公式，这里也还是适用的。如果每次分区操作，都能正好把数组分成大小接近相等的两个小区间，那快排的时间复杂度递推求解公式跟归并是相同的。所以，快排的时间复杂度也是 O(nlogn)。公式如下：
T(1) = C； n=1 时，只需要常量级的执行时间，所以表示为 C。
T(n) = 2*T(n/2) + n； n>1
但是，公式成立的前提是每次分区操作，我们选择的 pivot 都很合适，正好能将大区间对等地一分为二。但实际上这种情况是很难实现的。比如一组数据原来已经是有序的，如果我们每次选择最后一个元素作为 pivot，那每次分区得到的两个区间都是不均等的。我们需要进行大约 n 次分区操作，才能完成快排的整个过程。每次分区我们平均要扫描大约 n/2 个元素，这种情况下，快排的时间复杂度就从 O(nlogn) 退化成了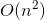 
。但是这种情况是一个比较极端的情况，我们可以对pivot指针进行优化来减少这种情况发生的概率，运用到前面文章讲到的均摊思想，其实时间复杂度就是 O(nlogn) 。
常见的基准选择有：选择第一个或最后一个、随机选择、三数取中等方法，性能上的优化也可以采用尾递归的方法来优化。
3、空间复杂度分析
由于快排并不像归并排序一样需要额外的数组来存储，所以空间复杂度是O(1)，是一个原地排序算法。
五、实战
本次实战的题目是如何在 O(n) 的时间复杂度内查找一个无序数组中的第 K 大元素？即在数组3，4，6，1，2，8，5，7，9中找出第三大的元素且时间复杂度为O(n)。
这道题可以利用快排来做，如果是单纯的排好再取的话，时间复杂度是O(n*logn)，显然与我们规定的O(n)的时间复杂度有出入，那如何压缩时间使得时间复杂度为O(n)呢？
在快排里每一步都是要分区的，我们可以利用这个思想，如果数组被分成a区和b区，a区都比b区小，那么如果k比b的长度小，则第k大的数就在b区种，我们则抛弃a区对b区利用快排进行分区。如果k比b的长度大，我们则反过来抛弃b区对a区利用快排进行分区。我们这里将上面的快排改写一下，主要改动的比较多是指针函数：
function quickSort(arr, start, end, maxK) {
var pivot = partition(arr, start, end);
if (pivot === maxK - 1) {
return arr[maxK - 1];
} else if (pivot > maxK - 1) {
return quickSort(arr, start, pivot - 1, maxK);
} else if (pivot < maxK - 1) {
return quickSort(arr, pivot + 1, end, maxK);
}
return 0;
}
function partition(arr, start, end) {
var temp = arr[start];
while (end > start) {
while (arr[end] < temp && end > start) {
end--;
}
if (end > start) {
arr[start] = arr[end];
start++;
}
while (arr[start] > temp && end > start) {
start++;
}
if (end > start) {
arr[end] = arr[start];
end--;
}
}
arr[start] = temp;
return start;
}这里面主要是将原来分区给反过来，按照之前所讲，分区后指针的右边都比指针大，左边都比指针小。但是这里为了得到第k大的数，则反过来，左边都比指针大，右边都比指针小。如果按照原来的思路的话，我们也可以很轻松的得到一个寻找第k小的方法：
function quickSort (arr, start, end, minK) {
var pivot = partition(arr, start, end)
if (pivot === minK - 1) {
return arr[minK - 1]
}
else if (pivot > minK - 1) {
return quickSort(arr, start, pivot - 1, minK)
}
else {
return quickSort(arr, pivot + 1, end, minK)
}
}
function partition (arr, start, end) {
var temp = arr[start]
var pt = arr[start]
while (start != end) {
while (start < end && arr[end] >= pt) {
end--
}
arr[start] = arr[end]
while (start < end && arr[start] <= pt) {
start++
}
arr[end] = arr[start]
}
arr[start] = temp
return start
}上一篇文章：数据结构与算法的重温之旅（九）——三个简单的排序算法
下一篇文章：数据结构与算法的重温之旅（十一）——桶排序、基数排序和计数排序
