引言

上一篇《前端工程师如何才能不焦虑？》发表后，很多小伙伴都评论说”何以解忧，唯有暴富“。这是一句实在话，正所谓焦虑也许不只是工作上，其实是生活。

但是大多数都是普通人，既不是富二代，也不是拆二代，又不能指望中个彩票一夜暴富，感觉上要走上财富自由之路遥遥无期。看着自己银行存款、每月要还的账单、日渐稀少的头发，想象着自己退休后的人生，是不是感觉更加焦虑了？

为了缓解焦虑，这篇文章会教大家打造一个工具，让大家可以通过理性、有迹可循的方式了解自己未来的财富情况，从而实现淡定的过好下半生。

怎样才算财富自由？

首先要回答的一个问题，到底多少钱才能算财富自由呢？

我们来看看一些媒体的报道，例如下图中提到的财务自由九个阶段，你到哪个阶段了？

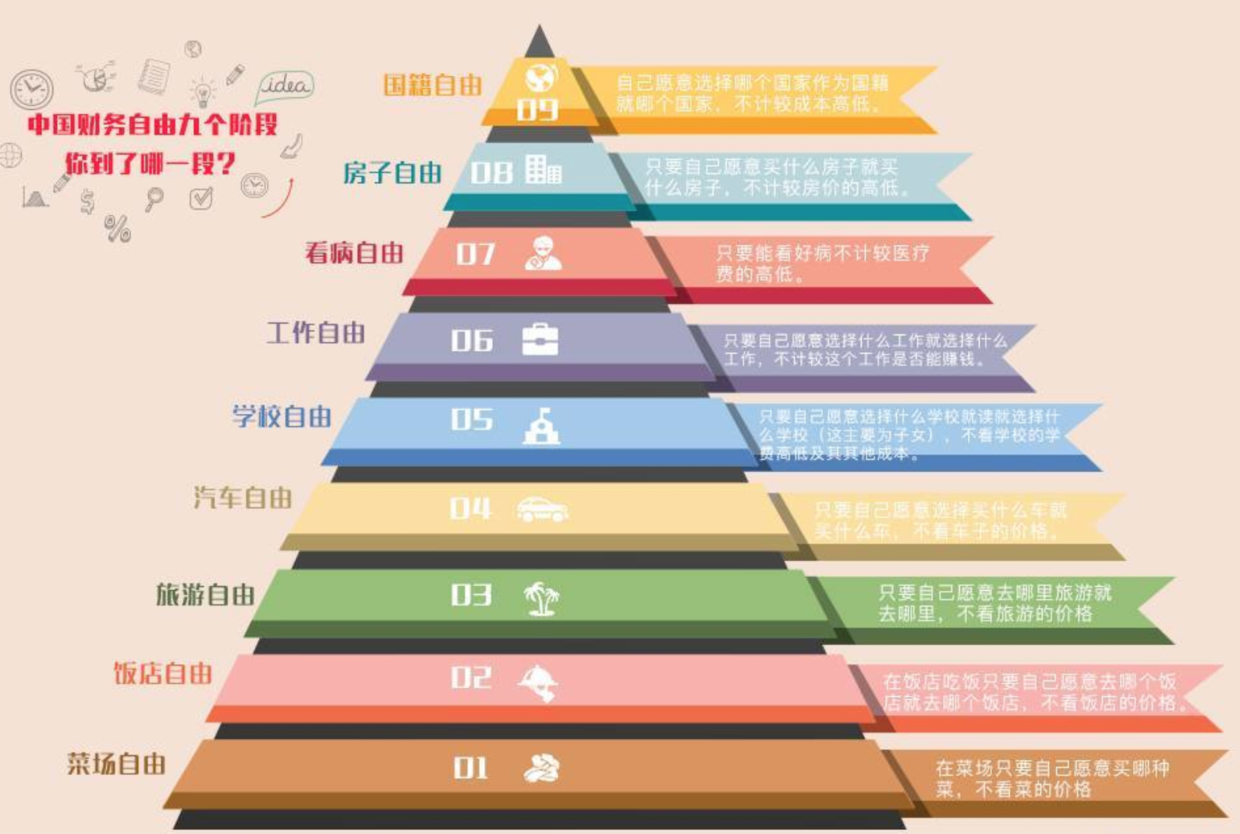
前阵子，胡润百富榜再次更新了北上广深等一线城市财务自由的衡量标准。根据胡润百富榜的统计数据显示，财富自由门槛比去年上涨50%，其中一线城市达到2.9亿，二线城市达到1.7亿。

1.7亿？2.9亿！看到这些标准，大家是不是准备洗洗睡了，感觉下辈子应该也赚不到这么多。但是，你是否想过到底怎样算是财富自由？我觉得这不应该是一个简单粗暴的数字，应该是一种状态，达到不用为了生活而必须工作的状态。

创造终身收入

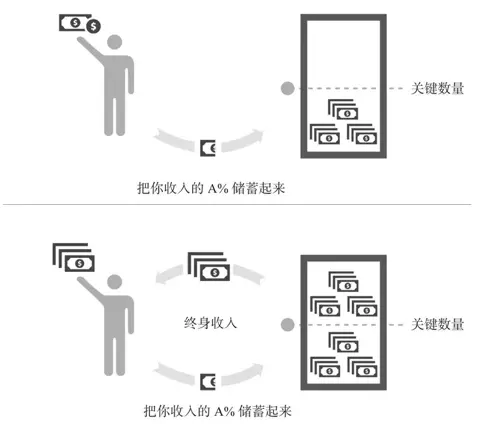
为了逃离赚的越多、花的越多的“老鼠赛跑”的困局，你需要打造一个可以创造终身收入的系统。每月把收入的固定比例储蓄起来，通过投资理财获取收益，直至达到关键数量，这时候产生的收益可以支持日常消费开销，从而打造出创造终身收入的系统。

每个人对于财富自由的定义都有不同的理解，但是我们需要对于打造终身收入所需要达到的关键数量有清晰的认识，而且越具体越好。

关键数量=每年的必须支出/(资产收益率-通货膨胀率)，例如每年必须支出20万，预期资产收益率8%，预期通货膨胀率3%，那么关键数量就是20/(8%-3%)=400万，牢牢记住这个数字以此为目标。

财富自由的公式

为了测算出未来的财富情况，需要通过一个可预期的公式来计算。现实情况可能非常复杂，为了简化我只列了几个因素：

当前年龄：理财从现在开始~
退休年龄：意味着没有了工资性收入
预期寿命：算算财富是否可以支撑你这一辈子
预期通胀率(%)：通胀率是个很可怕的东西，不要忽略
预期收益率(%)：收益率是个很可爱的东西，幻想自己是下一个巴菲特，年化20% Yeah~~
当前资金：启动资金
每年投入：工作期间，每年剩余可以再投入理财的资金
退休每年使用：退休后每年需要使用的资金，用于保障退休的生活质量

其实计算的逻辑是比较简单的，以退休为分界线：

第一年资产(工作中)：当前资金*(1+收益率-通胀率) + 每年投入
第二年资产(工作中)：第一年资产*(1+收益率-通胀率) + 每年投入
...
第n年资产(工作中)：第n-1年资产*(1+收益率-通胀率) + 每年投入
第n+1年资产(退休中)：第n年资产*(1+收益率-通胀率) - 退休每年使用
...
第xx年资产(退休中)：第xx-1年资产*(1+收益率-通胀率) - 退休每年使用

这个公式为了简化计算，有不少理想化的假设的

工作和退休的时间是分割的比较明确，但现实世界可能并不是如此。现实中可能你会有多段工作经历，中间会有间隔时间。
收益率和通胀率都是保持一个固定水平的。现实显然不是这样的，但可以用平均数来估算。
每年投入资金是固定的。现实显然也不会这样，随着工作经验提升，收入会增加，不过相应支出也会增加，每年投入资金可以用一个近似预估数目来替代。

Talk is cheap, show me the code

！！前方高能，如果对代码实现不敢兴趣可以略过，有兴趣的同学可以帮我找bug

核心计算每年资产的逻辑代码如下：

let mounts = [{ age: this.currentage, mount: this.currentmount }];
for (let i = 1; i <= this.retireage - this.currentage; i++) {
    let mount =
      (mounts[mounts.length - 1].mount + this.inputmount) *
      (1 + this.interestrate/100 - this.inflaterate/100);
    mounts.push({ age: this.currentage + i, mount: mount });
}

for (let i = 1; i <= this.lifeage - this.retireage; i++) {
     let mount = (mounts[mounts.length - 1].mount - this.usemount) *
      (1 + this.interestrate/100 - this.inflaterate/100);
      mounts.push({ age: this.retireage + i, mount: mount });
}
   
return mounts;

使用了一个数组mounts，数组内每一个元素都是一个map，key是年龄，value是资产。以退休年龄为分界线，分别计算每年的资产情况。

然后用echarts把数据渲染出来即可：

export default {
  name: "FinanceChart",
  props: ["tableData"],
  data() {
    return {
    };
  },
  computed: {
    orgOptions: function() {
      let xData = [];
      let yData = [];

      this.tableData.forEach(element => {
        xData.push(element.age);
        yData.push(element.mount);
      });

      let options = {
        xAxis: {
          type: "category",
          data: xData,
          name: '年龄'
        },
        yAxis: {
          name: '资产',
          type: "value",
          axisLabel: { interval:0, rotate:40 },
          axisLabel: {
            margin: 2,
            formatter: function (value, index) {
                if (value >= 10000 && value < 10000000) {
                    value = value / 10000 + "万";
                } else if (value >= 10000000) {
                    value = value / 10000000 + "千万";
                }
                return value;
            }
          }
        },
        series: [
          {
            data: yData,
            type: "bar",
            smooth: true
          }
        ]
      };

      return options;
    }
  }
};

有趣的数据

基于这个系统，我们先来体验一些有趣的数据

复利的力量

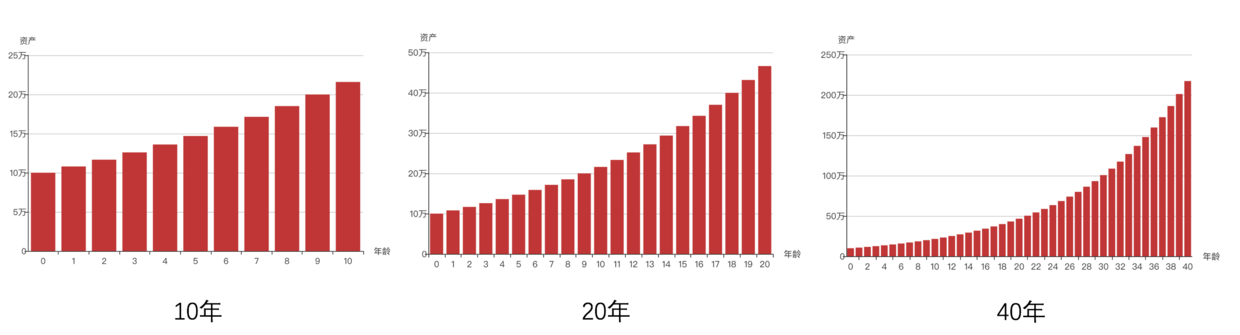
我们假设初始资金10万，每年除去通胀收益率8%，下面是10年、20年、40年的情况。10年时间会变成20多万，20年会变成40多万，40年后会变成200多万，这就是复利的力量！

耐心是一个非常重要的东西，财富的积累往往不是靠短时间内的爆发，需要长期稳定的积累才能看到效果，这个时间往往就是人的一辈子:)

利率的差别

一点点微小的利率差别可能在短期内看不到区别，但放在一个长时间维度，差距是非常巨大的。下面做个小实验比较下：

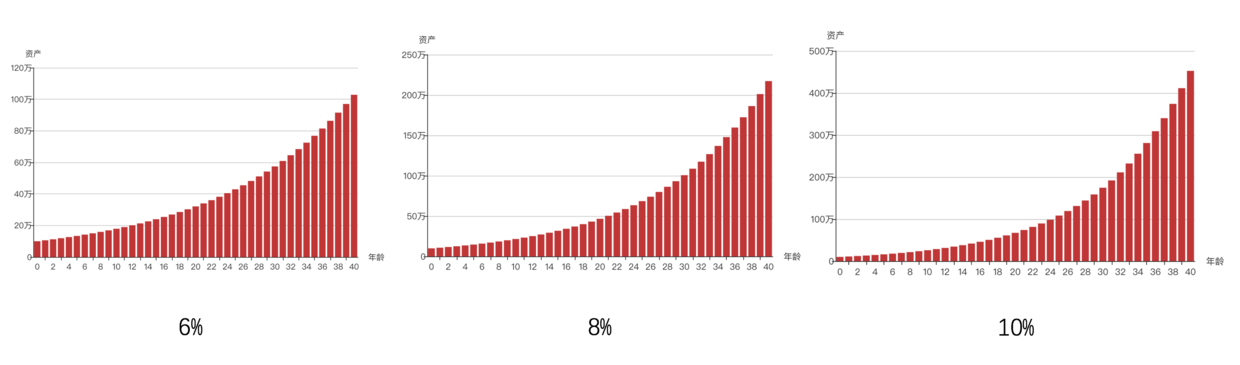
每年收益率每增加2%，放在40年的维度来看，最后都会有翻倍的效果，因此如何获得一个微小的收益提升都是非常关键重要的。一个小提示：关注一下自己购买的基金等理财产品，看下机构收取的手续费、管理费等等，千万不要小瞧了那1%-3%的费用。

模拟下真实的数据

来来来，让我们来模拟人生一把，看怎样才能过上财富自由的人生。

A同学，公务员工作稳定，25岁，假设他初始资金10万，每年还能再投入5万，理财收益能达到8%，工作到60岁退休，预计能活到90岁。

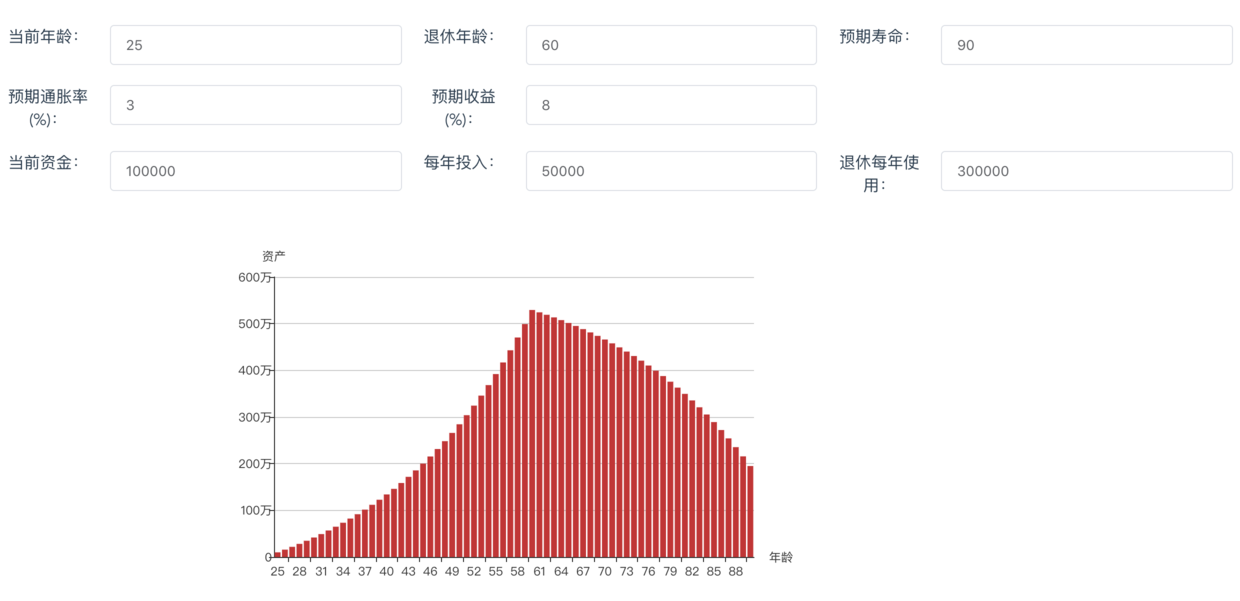
可以看到在退休年龄资产达到最高峰500万，随后每年花销30万依旧能很好满足未来的退休生活。

B同学，年轻码农，25岁，假设他初始资金10万，每年还能再投入10万，理财收益能达到8%，工作到50岁(还能做码农不？还是40岁退休？)退休，预计能活到85岁(寿命短些，扎心了)。

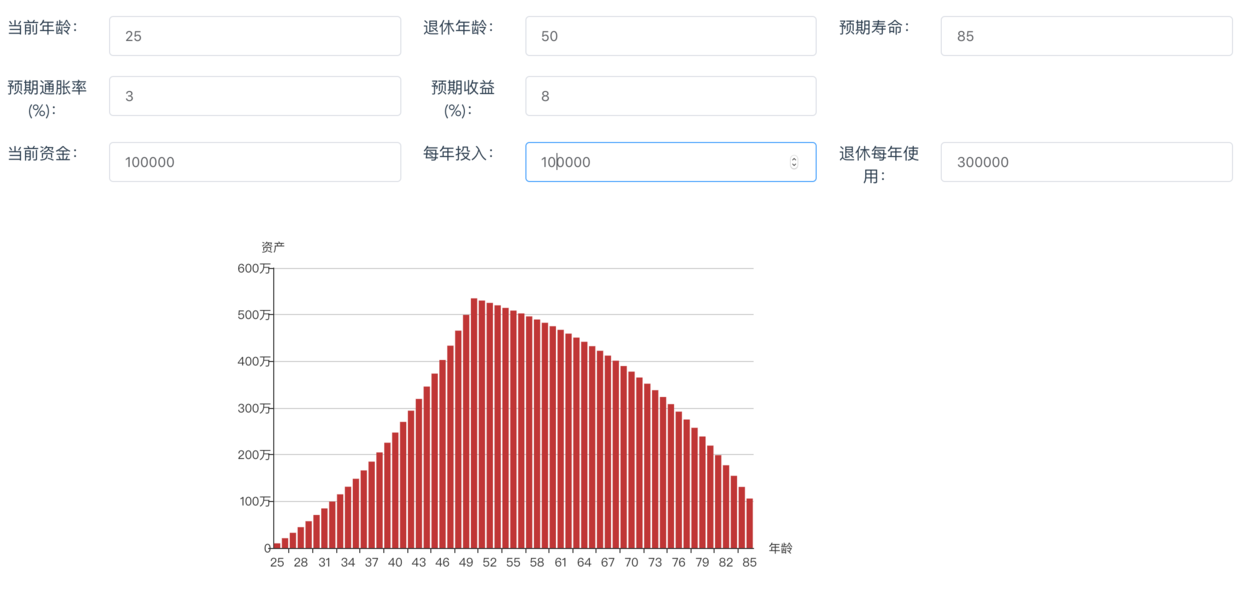
按照上述模型，完美度过无忧无虑的一生。But，要是只能干到45岁呢？em... 如果退休后还是要保持每年30万的开销，大约65岁就会断粮了。。。

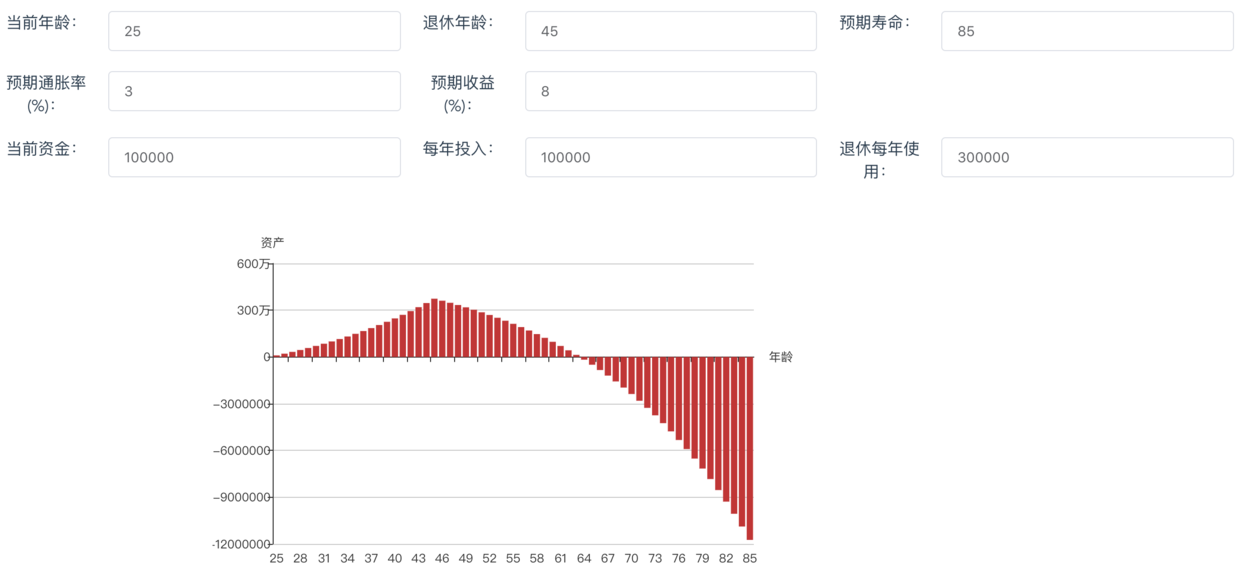
C同学，资深码农，35岁，假设他初始资金50万，每年还能再投入20万，理财收益能达到8%，工作到50岁退休，预计能活到85岁。

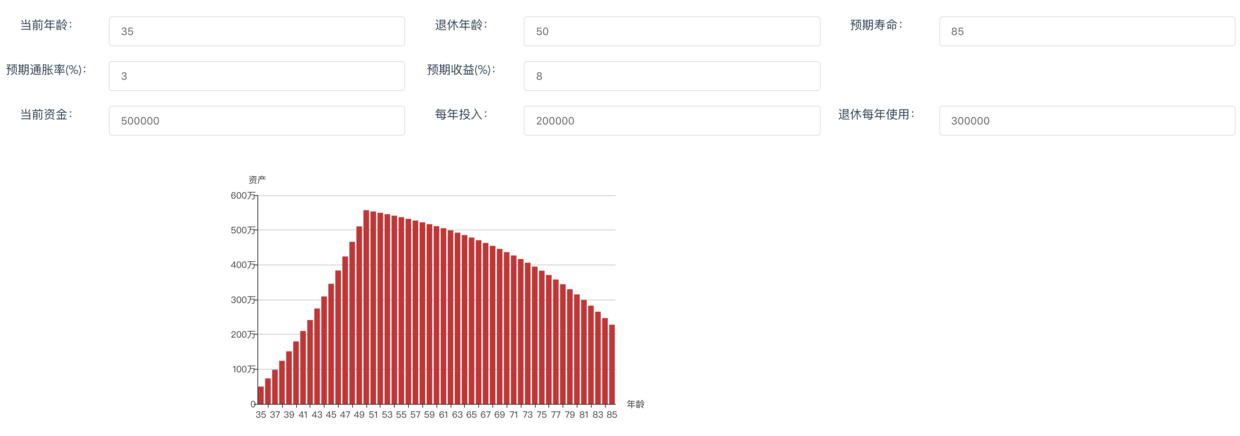
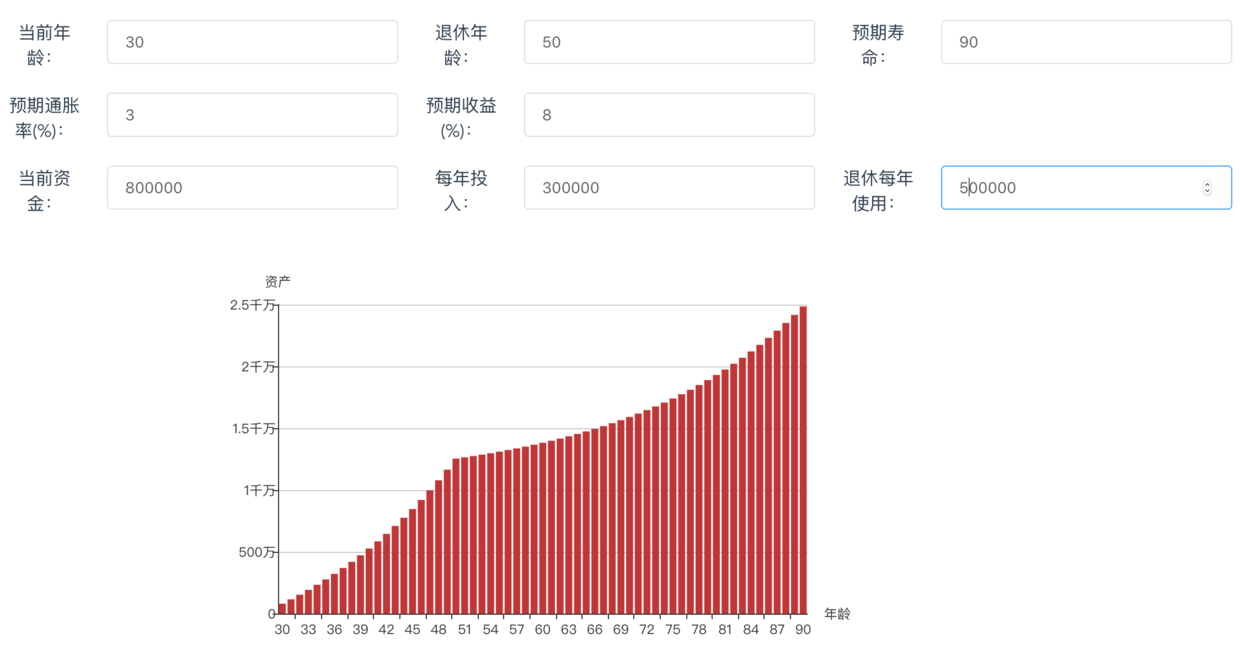
D同学，斜杠青年，30岁，假设他初始资金80万，每年还能再投入30万，理财收益能达到8%，工作到50岁退休，预计能活到90岁。

可以看到在退休前，他已经远远超过支持他退休所需要资产的关键数量，即使退休后没有新增资金，每年的资产依旧是增加的。人生赢家应该就是这位兄弟啦~~

写在最后

实现财富自由自然是每个人的梦想，人总是要有梦想的嘛，万一实现了呢。看到这里，其实大家也会发现要想过好这一辈子并没有想象中那么困难。

这里提炼我个人觉得几个关键点：

活的长：复利是靠时间积累出来的，巴菲特为什么成为股神，一个核心原因是他活的比其他股神时间长。
投的长：大家可以看到这个模型的基础是除去退休后使用资金，其他时候永远不会动用投资的资金。巴菲特也说过类似的话，对于持有好公司股票的期限应该是永远。
省的多：初始资金和每年投入资金极大的影响退休时候的资产情况，因此要保证固定比例的投资至关重要。
收益稳定&高：复利的基础是要有稳定且跑赢通胀的收益率，如果收益大幅波动长期而言资产积累是有限的，而且在波动中心态很难平稳度过，大概率会在低估割肉出局。如何保证投资收益稳定且高，这个是世界性难题，股神巴菲特也就达到年化20%左右，所以不要盲目追求高收益。

最后，祝大家好好学习，天天向上，早日上市，迎娶白富美，走上人生巅峰，通向财富自由之路。

悄悄给自己算了一下，em...，还是抓紧搬砖去啦~~

有兴趣同学可以关注微信公众号奶爸码农，不定期分享关于投资、理财、IT的信息：

何以解忧，唯有暴富，手把手教你打造财富方程式

引言