Qtum研究院：预编译合约及其在隐私资产中的应用

1、智能合约

以太坊中存在外部账户和合约账户两种，外部账户（Externally Owned Account, EOA）是被私钥控制且没有任何代码与之关联的账户。而合约账户(Contract Account, CA)是给智能合约分配的账户，被合约代码控制且有代码与之关联。外部账户可以发送交易，这个交易可以是转账交易，也可以是和智能合约有关的交易，用于创建智能合约或者触发智能合约。

以太坊的每笔交易Transaction会被转换成一个Message对象，传入EVM中执行，随后EVM将Message对象转换成Contract对象。如果是一笔普通转账交易，那么直接修改 StateDB 中对应的账户余额即可。如果是智能合约的创建或者调用，则通过 EVM 中的解释器加载和执行字节码，执行过程中可能会查询或者修改 StateDB。从图中可以看出，Contract对象会根据合约的地址，从数据库中加载相应的合约代码，然后送入解释器中进行执行。

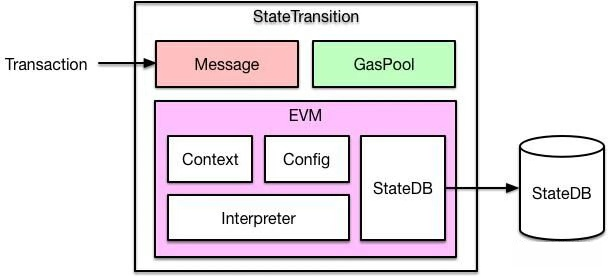
生成Message对象

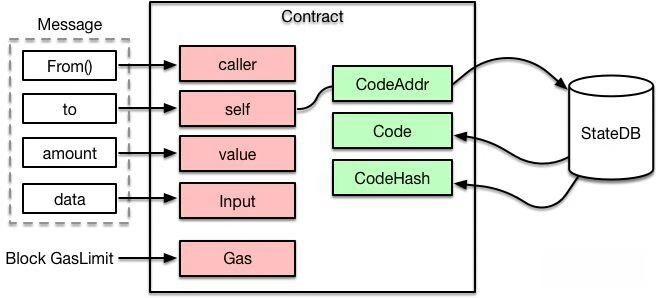
生成Contract对象

EVM解释器是一个基于栈式的机器，它有自己的PC、堆栈、内存和Gas池。一份合约代码会被解释为一条条OPCode，然后执行。在执行OPCode之前会检查该命令所需要的Gas和当前所剩Gas，如果Gas不足，则会返回ErrOutOfGas错误。因为EVM是基于栈的虚拟机，他没有寄存器之类的中间存储，所有的操作都要通过一个栈来进行维护，所以它的运行效率比较低，完成一个复杂操作可能需要较长的时间。更复杂的操作可能无法在有效时间执行完毕。具体可参见[1]。

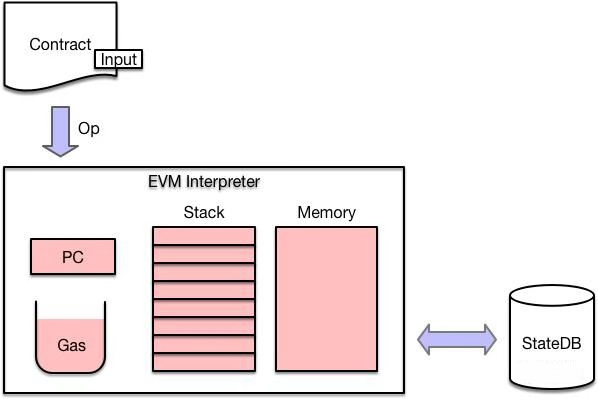
EVM interpreter内部逻辑

2、隐私资产

区块链是公开的分布式交易账本，链上的数据都是公开可见的，虽然一笔交易的发送方和接收方无法和现实生活中买卖双方进行关联，但是可以通过对链上的数据进行地址聚簇分析，从而得出一些地址和身份的关联信息。且交易的金额在链上也是公开的，可见尽管数据的公开透明保证了账本真实和不可篡改的特点，但是这也使得很多需要隐私的场景无法在区块链上进行运用。

在此背景下，隐私资产的概念被提出。通过使用密码学等技术手段将交易的发送方、接收方和交易金额进行隐藏，而矿工(验证交易者)可以在不需要知道具体数据的情况对一笔交易的合法性进行验证。常用的隐私资产实现的方法有Mimble-Wimble、ZK-SNARK等。

由于合约模式的广泛使用，一些项目方想到可以通过使用智能合约来实现隐私交易，如Nightfall、Zether、AZTEC等，通过部署和隐私交易有关的智能合约来达到在链上发行隐私资产的目的。

1、预编译合约的概念

因为EVM是基于栈的虚拟机，它根据操作的内容来计算gas，所以如果牵涉到十分复杂的计算，把运算过程放在EVM中执行就可能十分地低效，同时消耗非常多的gas。比如在zk-snark中，需要进行椭圆曲线的加减和配对运算，这个过程十分复杂，放在EVM中执行是不现实的。这就是以太坊提出预编译合约的初衷。

预编译合约是EVM中为了提供一些不适合写成opcode的较为复杂的库函数（多用于加密、哈希等复杂运算）而采用的一种折中方案，适用于合约逻辑简单但调用频繁，或者合约逻辑固定而计算量大的场景。预编译合约通常是在客户端用客户端代码实现，由于不需要使用EVM，所以运行速度快。对于开发者来说比直接使用运行在EVM上的函数消耗更低。

现在以太坊已经实现的预编译合约如下：

从代码层面来看，所谓的地址其实就是合约数组的下标，一个下标标识了一个预编译合约。其中和隐私算法有关的三个预编译合约是bn256Add()、bn256ScalarMul()、bn256Pairing()。

2、预编译合约的实现

在evm.go文件中，封装着evm的操作逻辑，里面有4个函数用于调用智能合约，Call()、CallCode()、DelegateCall()、StaticCall()。这四个函数做的工作都是生成一个contract对象，但是具体的细节如参数等会有一些差异。contract实例化之后，都是调用evm.go中的run函数来运行智能合约。该函数对预编译合约和非预编译合约调用两种情况均有考虑。下面的代码中，第一个分支是当该合约是一个预编译合约的时候，通过指定precompiles这个数组变量的下标来指定某一个预编译合约，从而实例化p参数。此处数组的下标其实就对应了预编译合约数组声明时地址的概念。之后调用RunPrecompiledContract函数来执行预编译合约。而如果是非预编译合约，从代码中可以看到是调用了evm的解释器进行执行。

go-ethereum/core/vm/evm.go

在RunPrecompiledContract函数中，可以看到p变量实现接收器进行bn256曲线加的操作，然后将结果进行返回。可以很明显地看到这部分操作是在客户端语言的执行过程中进行计算的。具体可参见[2]。

go-ethereum/core/vm/contracts.go

go-ethereum/core/vm/contracts.go

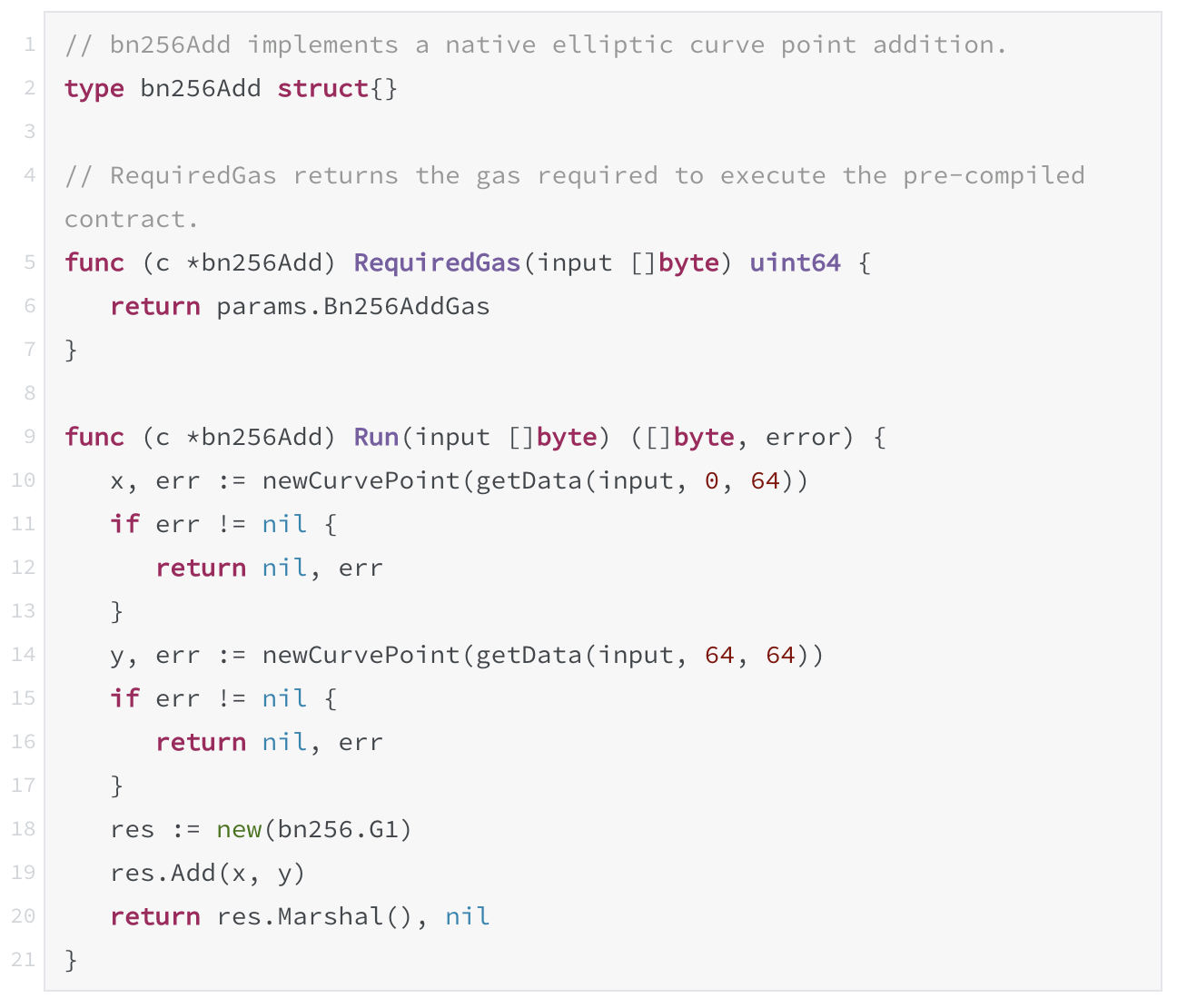
3、预编译合约的使用

在智能合约代码中，预编译合约也像普通的合约一样，可以直接在合约文件中进行调用，但调用方式有一些不同。通过在.sol文件中注明一个assembly代码块进行预编译合约的调用。调用规范和调用的参数如下所示。

一个实现椭圆曲线加法的实例如下

1、椭圆曲线的预编译合约

以太坊现在处理隐私的解决方案是使用zk-snark[6][8]，但是zk-snark是一个及其复杂的数学过程，里面牵涉到很多椭圆曲线的计算。经过前面的分析，这个过程放在evm里面执行是十分不现实的，所以为了支持zk-snark的相关运算，以太坊分别在EIP196[3]和EIP197[4]里增加了三个与zk-snark运算有关的预编译合约，可以供开发者调用。

EIP-196增加了在alt_bn128曲线上的ECADD()和ECMUL()两个预编译合约，其中ECADD()消耗500gas，ECMUL()消耗40000gas。

EIP-197增加了在alt_bn128曲线上的配对Pairing函数，消耗gas为80000*k+100000(k和点对个数有关)。

椭圆曲线上的加和乘比较好理解，pairing的出现是因为zk-snark中有KCA(Knowledge of Coefficient Test and Assumption)认证过程[6]，需要用到双线性映射来进行证明，具体可参见V神medium[7]。Pairing就是证明过程中会用到的公式。Pairing函数的输入是一个不定长的列表，因为不同的zk-snark算法可能数据量是不同的，并且pairing函数所消耗的gas也与输入的点对个数有关。

现在许多利用预编译合约实现隐私的算法都使用到了pairing过程，例如EYBlockchain、AZTEC等。pairing是ZK-snark所必须要求的一个步骤，耗费的gas巨大，当然官方也在做优化。实现pairing的过程一般要在pairing-friendly曲线上来进行，这是一类具有特殊属性的曲线，主要表现在计算pairing速度很快。所以如果要用pairing这个过程，那么常用的secp256k1这样的曲线显然是不适合的，就需要增加对pairing-friendly曲线的支持。

现在主流的pairing-friendly曲线有Barreto-Naehrig(BN)系列和Barreto-Lynn-Scott(BLS)系列[9]，以太坊使用的就是BN系列，ZCASH使用的是BLS系列，以太坊后续也会加上对BLS曲线的支持。BLS的曲线综合表现会好很多，计算量也相对较小。但是不管怎么样，选择曲线都有安全和效率之间进行平衡的一个取舍。

值得一提的是，如果不需要用到pairing过程，也就不需要pairing-friendly曲线。另外一种方案是增加对secp256k1曲线的预编译合约的支持。例如PGC团队虽然使用了bn256ADD和bn256MUL两个预编译合约，即使用了bn系列的曲线，但是他们的算法是不需要pairing的，如果换成对secp256k1的预编译合约支持会对算法效率有提高。

针对于C++版本实现的问题，现在主要有两个外部库对这些操作进行了封装和实现。首先是Libff，这也是现在以太坊正在 使用的库，源码中LibSnark.cpp调用了libff库的相关计算函数。还有一个是MCL库，这是EIP-1108所推荐的库。

2、隐私资产项目

现在在业内比较流行的四个隐私解决方案是EYBlockchain、PGC、Zether、AZTEC。

EYBlockchain是基于以太坊zk-snark零知识证明实现的隐私资产。它通过移植以太坊推荐的ZoKrates工具包进行线下的零知识证明的生成。算法需要用bn256曲线的add、multiply、pairing过程。一笔转账Gas消耗在2.7M左右。

Zether是一个以太坊上的匿名支付协议，以智能合约 Zether Smart Contract（ZSC）的形式部署在以太坊上，并且具有称为 Zether 令牌（ZTH）的代币，其可作为 ElGamal 公钥的 Zether 账户之间传输的载体，并支持匿名的智能合约交互。算法需要用到bn256曲线的add、multiply算法。

PGC是改进版的Zether算法，PGC使用原版的Elgamal和原版的bulletproof零知识证明算法。PGC使用了bn256曲线的add、multiply算法，但是，如果secp256k1椭圆曲线的预编译合约可以实现，那么PGC算法可以不使用bn系列的曲线。

AZTEC结合同态证明和range proof提供零知识证明，以在以太坊上提供隐私资产。AZTEC需要使用bn256曲线上的add、multiply、pairing操作，具体操作量为(3n+m-1)add+(2n+2m-2)multiply+1pairing(n和m分别是交易票据的数量)。

3、gas问题

EIP-196和EIP-197的提出，使得很多零知识证明的算法可以在以太坊上运行。但还是有一个问题，尽管把这些复杂的数学过程通过预编译合约的方式来实现，它所消耗的gas还是十分巨大，不夸张地说，在某些场景下，转账一笔隐私资产所消耗的Gas可能比转账的金额还要高。以太坊每个block的最多gas消耗为8M，这就使得很多隐私的项目无法真正地落地。

为了降低预编译合约的gas，AZTEC的员工提出了EIP-1108[5]的改进。

EIP-1108是对add、mul、pairing这三个预编译合约所做的一个优化，通过对调用库的底层算法进行优化，提高了代码的运行效率，从而降低了gas。Golang版本的预编译合约名也变成了bn256。bn256就是alt_bn128，只是更换了一个说法。256是指公式中p的长度，而128是指曲线的安全等级。这是一条曲线的两个不同的属性描述。所以EIP-1108并不是更换了曲线降低了gas，而是对实现的算法进行了优化。更新后的gas对比图如下。EIP-1108目前处于draft的状态，代码中算法部分已经进行改进，但是gas的值还没有进行更新。

若使用EIP-1108的改进方法，许多隐私资产的算法可以得到大大的优化。Zether一笔转账交易gas消耗可从7188000减少到1700000。PGC一笔转账交易gas消耗可从6563000减少到1100000。AZTEC则从121000n+41000m+219000降低到12200n+6200m+85930。

如果要部署预编译合约，如何确定预编译合约的Gas值是一个严峻的问题。预编译合约gas的设置是和操作的计算量有关的，例如EIP-1108中介绍了Pairing gas的计算方法。它是根据ecrecover的效率和既定gas来决定的。一次ecrecover调用需要花费116ms，它的gas被设置成了3000，这样得到了1ms运行花费25.86gas的事实。因为pairing计算花费的时间分为两个部分，一个是基时间base_tim，可以理解为运算的启动时间，还有一个是浮动时间per_pair_time，它和输入的计算量有关。计算1个pairing需要耗费3037ms，计算10个pairing耗费14663ms。得出base_time和per_pair_time，乘以既定好的25.86gas，得出pairing过程的gas消耗。如此，则可以根据具体的环境做相关的benchmark以规范gas的设置。

Qtum每个block的最多gas消耗为40M，每个transaction的最多gas消耗为20M，因此隐私资产在Qtum上运行基本不会受到gas的限制。但是使用EVM去运行一些计算量大的隐私算法是非常低效的。所以，未来将会把一些基础的、通用的隐私算法做成预编译合约的形式，让隐私资产能够更加高效地运行在Qtum上，也节省了合约的开发工作。

对于椭圆曲线而言，下一步可以考虑增加BLS和secp256k1椭圆曲线的预编译合约。BLS的性能和安全性都优于bn256，且是pairing-friendly，所以可以用于代替bn256。并且如果要部署pairing预编译合约，也可以找一个已经定好gas的预编译合约进行参照，分别benchmark，进行类似的gas设定。secp256k1虽然不是pairing-friendly，但其性能更好，且通用性更强，广泛用于区块链的签名、加密算法中。

对于零知识证明而言，未来可以考虑增加Bulletproof算法作为预编译合约。Bulletproof是目前区块链中广泛使用的范围证明算法，主要用于证明MimbleWimble中隐藏的交易金额是一个正数。Bulletproof已经在Grin和Beam项目中实现并稳定运行。Bulletproof的验证过程计算量大，因此使用预编译合约实现是更为合适的选择。有了Bulletproof预编译合约之后，MimbleWimble就能以合约的方式高效地运行于Qtum上。

参考文献

[1]https://www.chainnews.com/articles/693606750348.htm

[2]https://blog.csdn.net/hello2mao/article/details/87254340

[3]https://github.com/ethereum/EIPs/blob/master/EIPS/eip-196.md

[4]https://github.com/ethereum/EIPs/blob/master/EIPS/eip-197.md

[5]https://github.com/ethereum/EIPs/blob/master/EIPS/eip-1108.md

[6] https://www.jianshu.com/p/7b772e5cdaef

[7]https://medium.com/@VitalikButerin/exploring-elliptic-curve-pairings-c73c1864e627

[8]https://medium.com/@VitalikButerin/zk-snarks-under-the-hood-b33151a013f6

[9]https://blog.csdn.net/mutourend/article/details/92784689