本文首发于微信公众号「程序员面试官」
数组几乎可以是所有软件工程师最常用到的数据结构,正是因为如此,很多开发者对其不够重视.
而面试中经常有这样一类问题: 「100万个成员的数组取第一个和最后一个有性能差距吗?为什么?」
除此之外,我们在平时的业务开发中会经常出现数组一把梭的情况,大多数情况下我们都会用数组的形式进行操作,而有读源码习惯的开发者可能会发现,在一些底层库中,我们可能平时用数组的地方,底层库却选择了另外的数据结构,这又是为什么?
希望大家带着以上的问题我们进行讨论.
什么是数组
数组是计算机科学中最基本的数据结构了,绝大多数编程语言都内置了这种数据结构,也是开发者最常见的数据结构.
数组(英语:Array),是由相同类型的元素(element)的集合所组成的数据结构,分配一块连续的内存来存储.
当然,在一些动态语言中例如Python的列表或者JavaScript的数组都可能是非连续性的内存,也可以存储不同类型的元素.
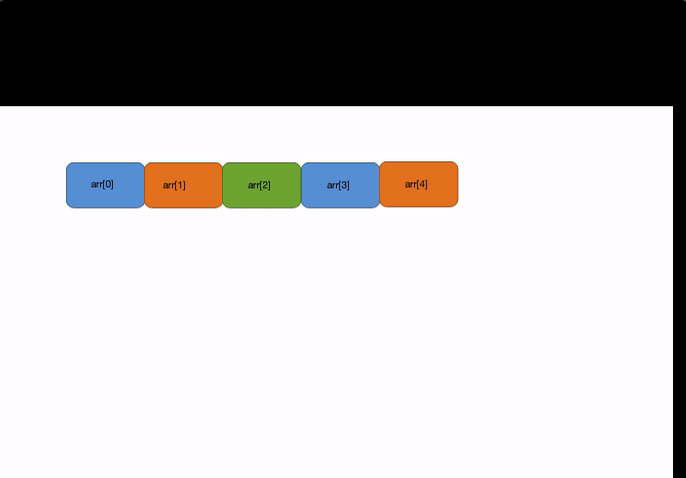
比如我们有如下一个数组:
arr = [1, 2, 3, 4, 5]
其在内存中的表现应该是这样的:
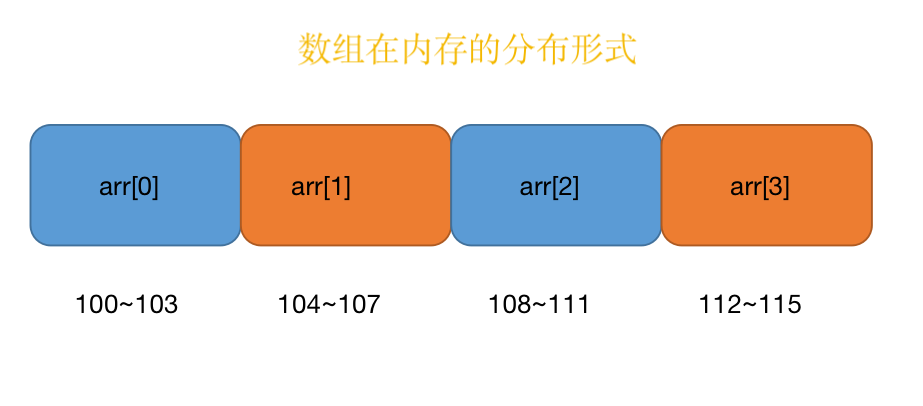
我们可以看到,这个数组在内存中是以连续线性的形式储存的,这个连续线性的储存形式既有其优势又有其劣势,只有我们搞清楚优劣才能在以后的开发中更好地使用数组.
数组的特性
一个数据结构通常都有「插入、查找、删除、读取」这四种基本的操作,我们会逐一分析这些操作带来的性能差异.
首先我们要辨析一个概念--性能.
这里的性能并不是绝对意义上速度的快慢,因为不同的设备其硬件基础就会产生巨大的速度差异,这里的性能是我们在算法分析中的「复杂度」概念.
复杂度的概念可以移步算法分析
插入性能
我们已经知道数组是一段连续储存的内存,当我们要将新元素插入到数组k的位置时呢?这个时候需要将k索引处之后的所有元素往后挪一位,并将k索引的位置插入新元素.
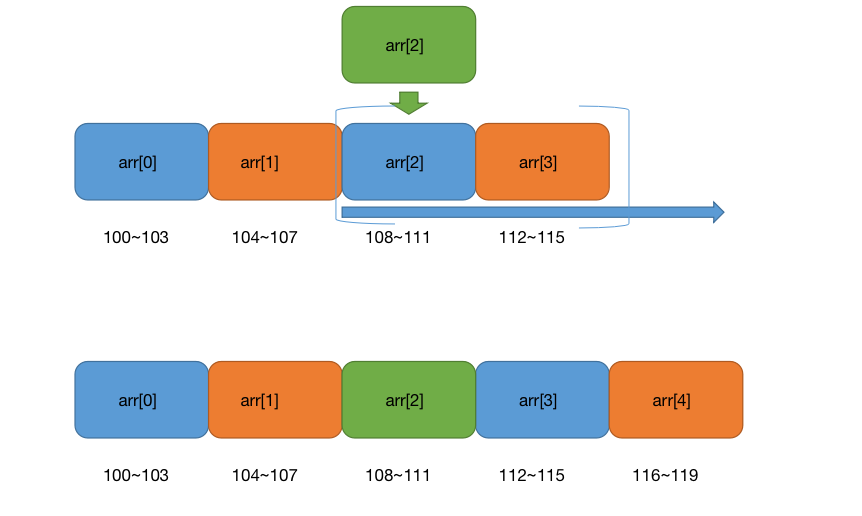
我们看到这个时候需要进行操作的工作量就大多了,通常情况下,插入操作的时间复杂度是O(n).
删除性能
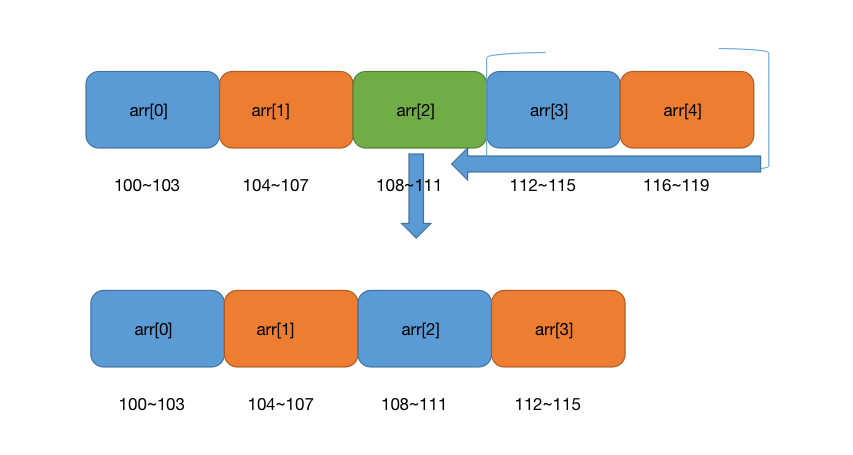
删除操作其实与插入很类似,同样我要删除数组之内的k索引位置的元素,我们就需要将其删除后,为了保持内存的连续性,需要将k之后的元素通通向前移动一位,这个情况的时间复杂度也是O(n).
查找性能
比如我们要查找一个数组中是否存在一个为2的元素,那么计算机需要如何操作呢?
如果是人的话,在少量数据的情况下我们自然可以一眼找到是否有2的元素,而计算机不是,计算机需要从索引0开始往下匹配,直到匹配到2的元素为止.
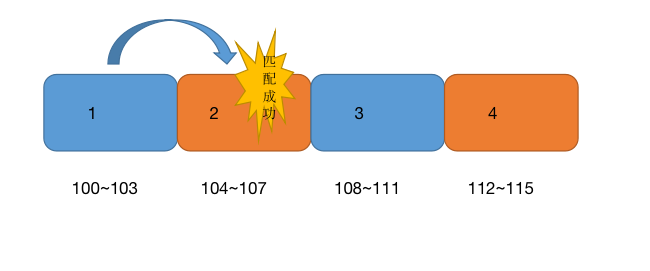
这个查找的过程其实就是我们常见的线性查找,这个时候需要匹配的平均步数与数组的长度n有关,这个时间复杂度同样是O(n).
读取性能
我们已经强调过数组的特点是拥有相同的数据类型和一块连续的线性内存,那么正是基于以上的特点,数组的读取性能非常的卓越,时间复杂度为O(1),相比于链表、二叉树等数据结构,它的优势非常明显.
那么数组是如何做到这么低的时间复杂度呢?
假设我们的数组内存起始地址为start,而元素类型的长度为size,数组索引为i,那么我们很容易得到这个数组内存地址的寻址公式:
arr[i]_address = start + size * i
比如我们要读取arr[3]的值,那么只需要把3代入寻址公式,计算机就可以一步查询到对应的元素,因此数组读取的时间复杂度只有O(1).
性能优化
我们已经知道除了「读取」这一个操作以外,其他操作的时间复杂度都在O(n),那么有没有有效的方法进行性能优化呢?
查找性能优化
当数组的元素是无序状态下,我们只能用相对不太快的线性查找进行查找,当元素是有序状态(递增或者递减),我们可以用另一种更高效的方法--二分查找.
假设我们有一个有int类型组成的数组,以递增的方式储存:
arr = [1, 2, 3, 4, 5, 6, 7]
如果我们要查找值为6元素,按照线性查找的方式需要根据数组索引从0依次比对,直到碰到索引5的元素.
而二分查找的效率则更高,由于我们知道此数组的元素是有序递增排列的:
- 我们可以取一个索引为3的元素为中间值p
- 将p与目标值6进行对比,发现p的值
4<6,那么此时由于是递增数组,目标值一定在索引3之后的元素中 - 此时,再在索引3之后到尾部的元素中取出新的中间值p与目标值比对,再重复下去,直到找到目标值
我们可以发现这样的操作每一次对比都能排除当前元素数量一半的元素,整体下来的时间复杂度只有O(log n),这表示此方法的效率极高.
这种高效的方法在数据量越大的情况下,越能体现出来,比如目前有一个10亿成员的数组是有序递增,如果按照线性查找,最差的情况下需要10亿此查找操作才能找到结果,而二分查找仅仅需要7次.
插入性能优化
比如有以下数组,我们要将一个新成员orange插入索引1的位置,通常情况下需要后三位成员后移,orange占据索引1的位置.
但是如果我们的需求并不一定需要索引的有序性呢?也就是说,我们可以把数组当成一个集合概念,我们可以在索引1的位置插入orange并在数组的尾部开辟一个新内存将原本在1位置的banana存入新内存中,这样虽然索引的乱了,但是整个操作仅仅需要O(1)的时间复杂度.
arr = ['apple', 'banana', 'grape', 'watermelon']
删除性能优化
删除操作需要将产出位置后的元素集体向前移动,这非常消耗性能,尤其是在频繁的删除、插入操作中更是如此。
我们可以先记录下相关的操作,但是并不立即进行删除,当到一定的节点时我们再一次性依据记录对数组进行操作,这样数组成员的反复频繁移动变成了一次性操作,可以很大程度上提高性能.
这个思想应用非常广泛:
- 前端框架的虚拟DOM就是将对DOM的大量操作先储存在差异队列中,然后再一次性更新,避免了DOM的回流和重绘.
- V8和JVM中的标记清除算法也是基于此思想,标记清除算法分为两个阶段,标记阶段对访问到的对象都打上一个标识,在清除阶段发现某个对象没有标记则进行回收.
小结
回到题目中的问题,我们现在已经可以很清楚地知道「100万个成员的数组取第一个和最后一个是否有性能差距」,答案显然是没有,因为数组是一块线性连续的内存,我们可以通过寻址公式一步取出对应的成员,这跟成员的位置没有关系.
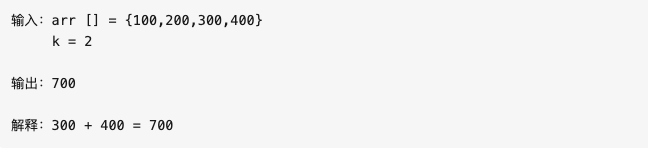
最后我们经常在面试或者LeetCode中碰到这样一类问题,即数组中的子元素问题.
比如: 给定一个整数数组,计算长度为 'k' 的连续子数组的最大总和。
什么方法可以尽可能地降低时间复杂度?说出你的思路即可.
