写在前边
上一篇文章我们讲解了二叉树的基础知识,什么是二叉树、二叉树的特点、二叉树的存储方式、二叉树的遍历等。基础归基础,理论归理论。最重要的最终还要和实践挂钩。
今天这篇主要分享一下二叉树的一些简单应用,二叉树涉及到的很多应用也是有难度的,比如红黑树、AVL 树、B+树等,这节不会涉及到。还需要自行深入探索。本篇希望能够给你带来二叉树的应用思考。
我们都知道上一节分享到了二叉树的遍历,那么二叉树还能干什么,数据结构之所以为数据结构,对数据进行操作的,查找、删除、插入等,那么二叉树对于这些操作是否更高效呢?
思维导图
1、什么是二叉查找树?
二叉树中能够实现快速插入、删除、查找的特殊二叉树就是二叉查找树了。前边我们讲了数组、链表、二分查找等,以后的文章还会有哈希表、跳表等也是用于数据的插入、查找等,那么二叉查找树又有哪些优势呢?
那什么是二叉查找树?为何实现快速的插入、删除操作?有了上一篇文章的基础,都是为这篇的二叉查找树做铺垫。二叉查找树的由来都是由二叉树的特点决定的。
但是二叉查找树又对其进行改进,要求在二叉查找树中左子节点必须小于根节点,而右子节点则大于根节点,这种特殊的二叉树就叫做二叉查找树。
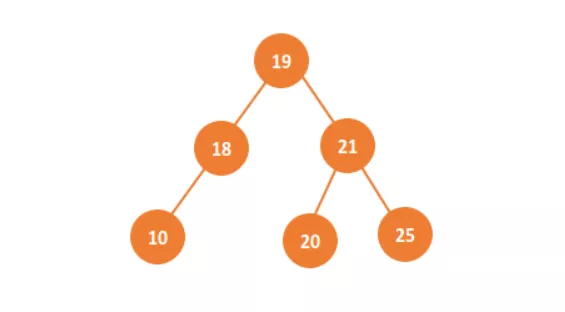
二叉查找树的定义非常简单,那么下面我们就见识见识二叉查找树的各种操作。
2、二叉查找树的插入操作
二叉查找树如何插入一个节点元素?因为们知道二叉查找树的特点,左子节点小于根节点右子节点大于根节点。插入一个元素,首先让该元素和根节点比较,如果小于根节点,就插入到左子节点位置,如果左子节点有数据,就继续和插入的数据比较大小,直到当前结点为叶子节点位置 —— 整个过程也是一个递归的过程。
动画实现:
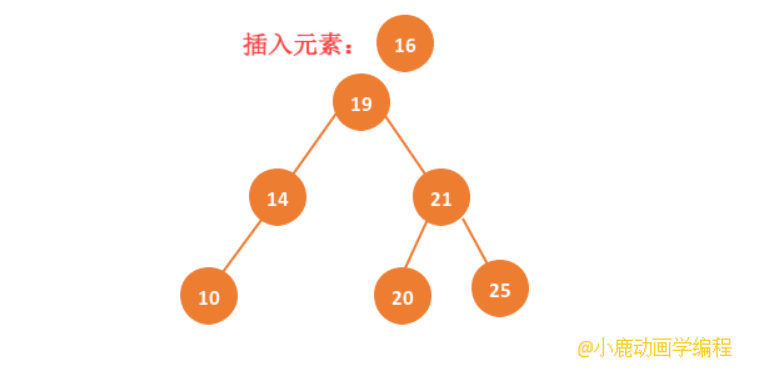
性能分析:
插入操作的时间复杂度跟整棵树的高度成正比,时间复杂度为 0(log2n)。
代码实现: JavaScript 版本
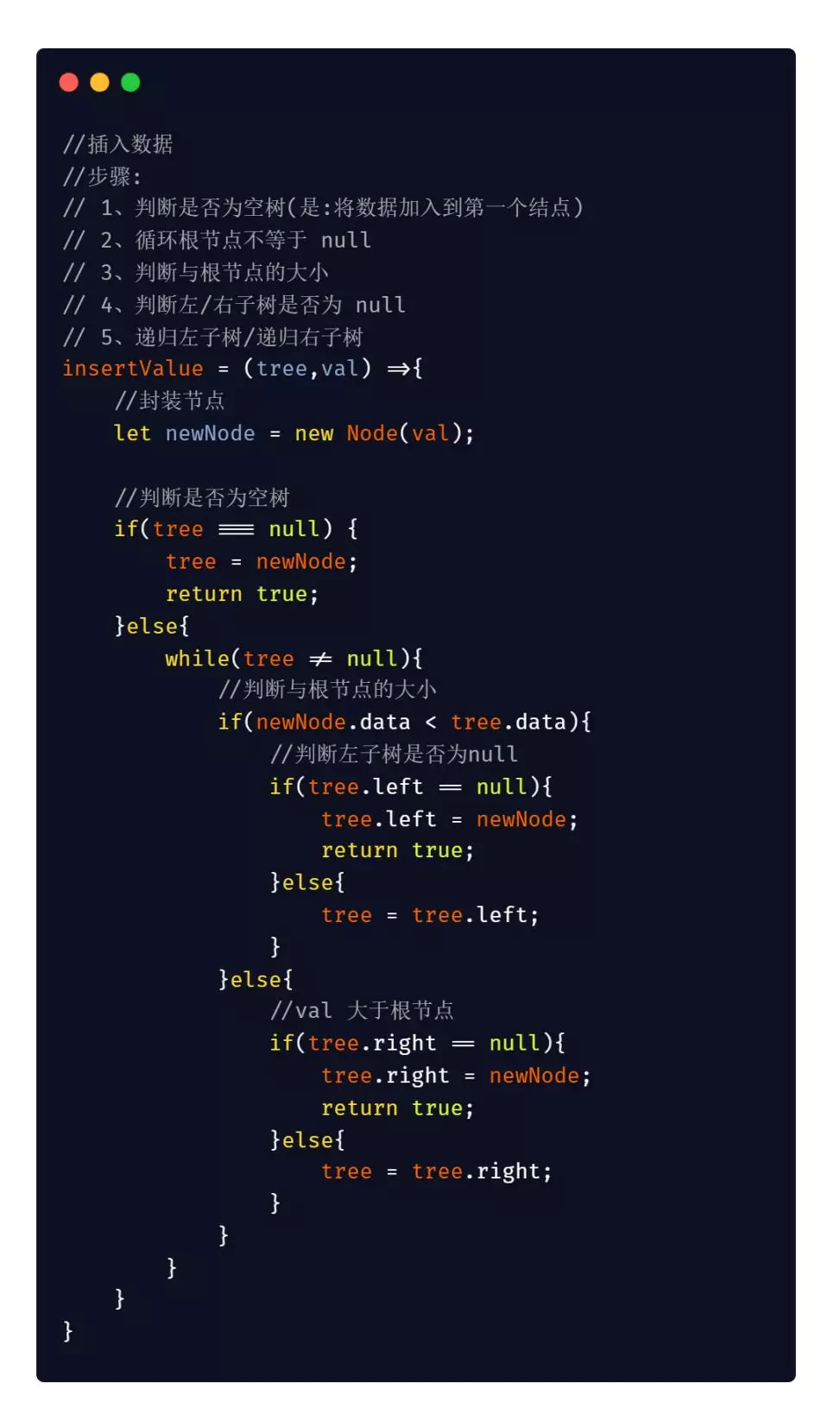
Java 版本
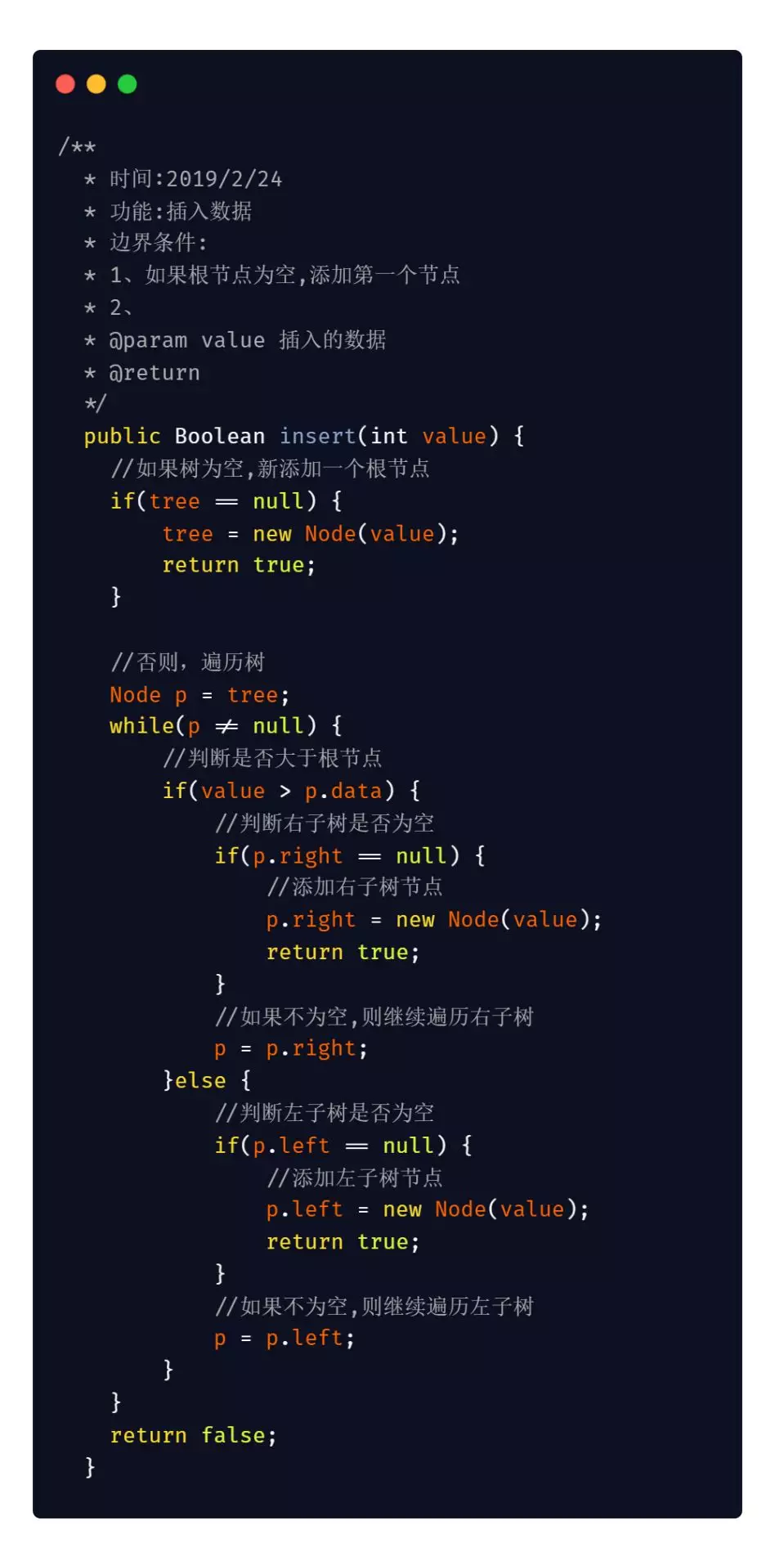
3、二叉查找树的查找操作
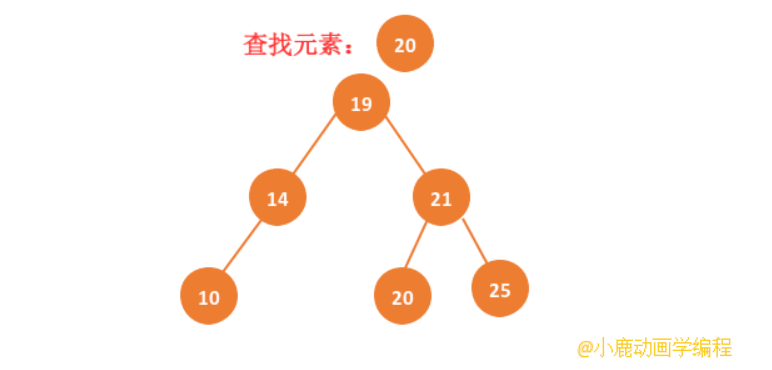
查找一个节点元素同样也是根据二叉查找树的特点进行查找,首先和根节点进行比较大小,小于根节点就在左子节点进行递归,否则在右子节点进行递归查找。如果查找到该元素与某节点相同,则可以返回该节点,否则继续递归直到查找完毕没有查找到。
动画实现:
性能分析:
查找的时间复杂度同样和二叉查找树的高度成正比,为 O(log2n)。
代码实现: JavaScript 版本

Java 版本

4、二叉查找树的删除操作
对于删除,我们想一想,会多多少少涉及一些边界条件。比如,二叉查找树只有一个根节点或者删除二叉查找树的叶子节点以及中间结点,我们写代码的时候要做的就是分别判断这几种情况,然后进行一一处理,这样说,逻辑听起来更清晰一点。
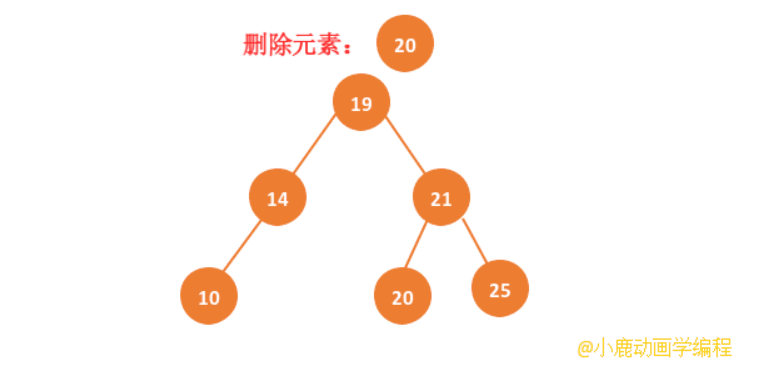
情况一:如果我们要删除树中的节点没有子节点,也就是说我们删除的节点为叶子节点的话,我们直接将叶子节点的父节点指向删除节点的指针设置为 null。
动画实现:
性能分析:
删除操作同样也是如此,时间复杂度为 O(log2n)。
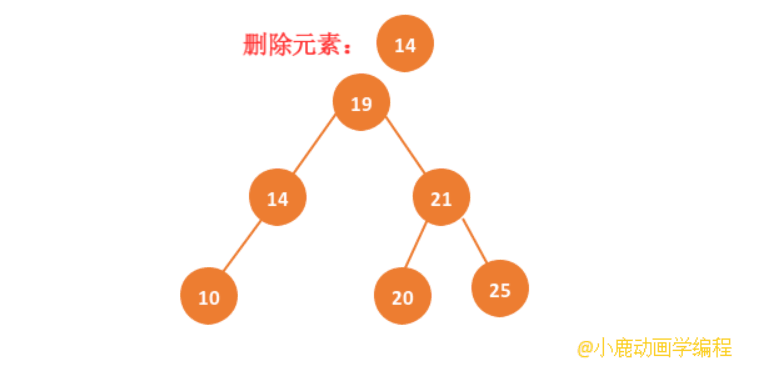
情况二:第二种情况就是,如果删除的节点下正好有一个节点(左子节点或者右子节点),直接将删除节点的父节点直接指向该删除节点的子节点。
动画实现:
情况三:如果删除的节点下有两个子节点就有点小复杂了,我们先来看如何操作,然后再解释原因。先将找到删除节点的右子树中递归找到最小的节点元素,将其替换我们要删除的节点。
因为删除节点的右子树最小的节点也要比删除节点的左子树要大,而且最小节点没有叶子节点,所以替换后还是符合二叉查找树的特点。
动画实现:
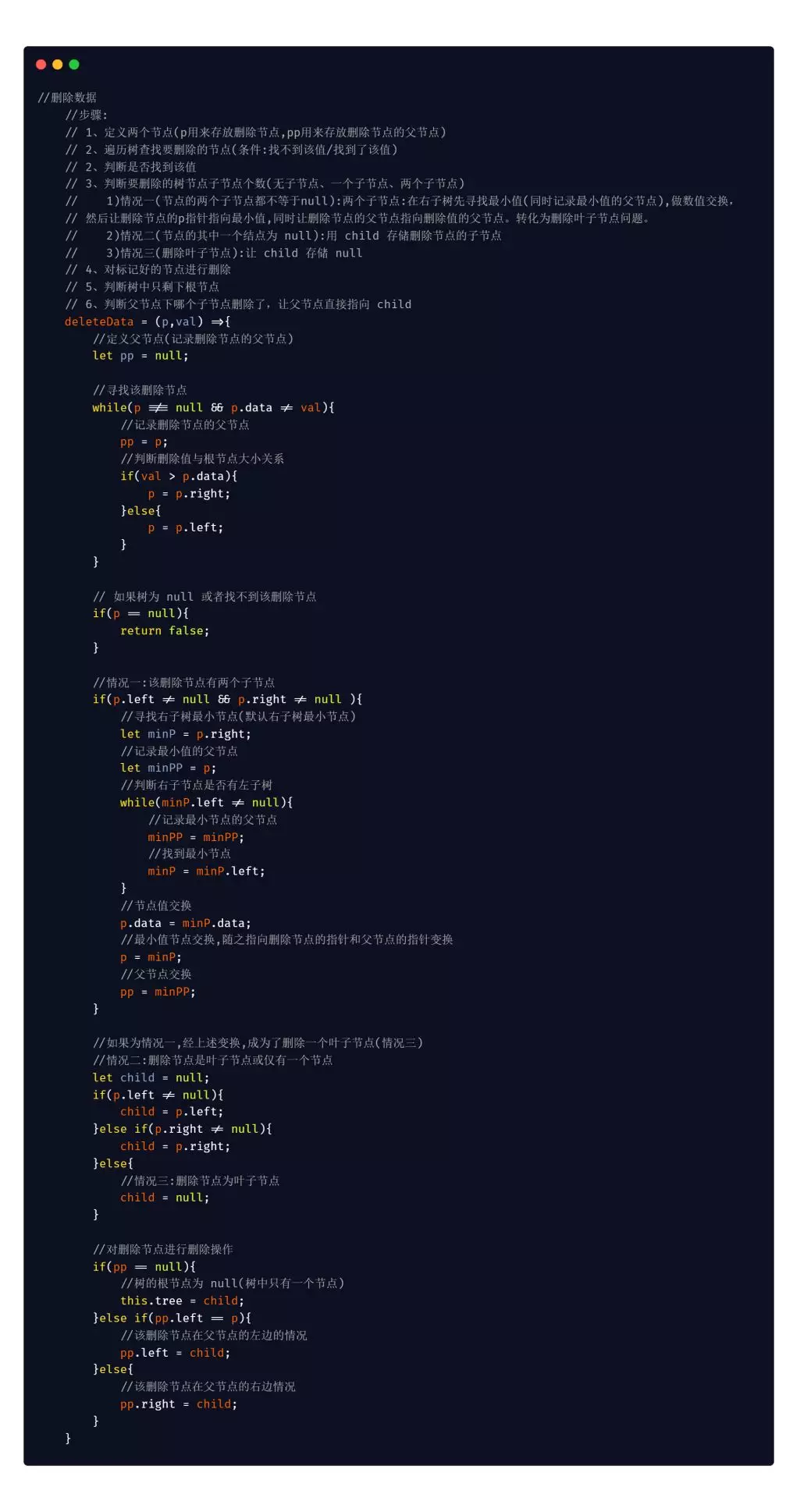
代码实现: JavaScript 版本
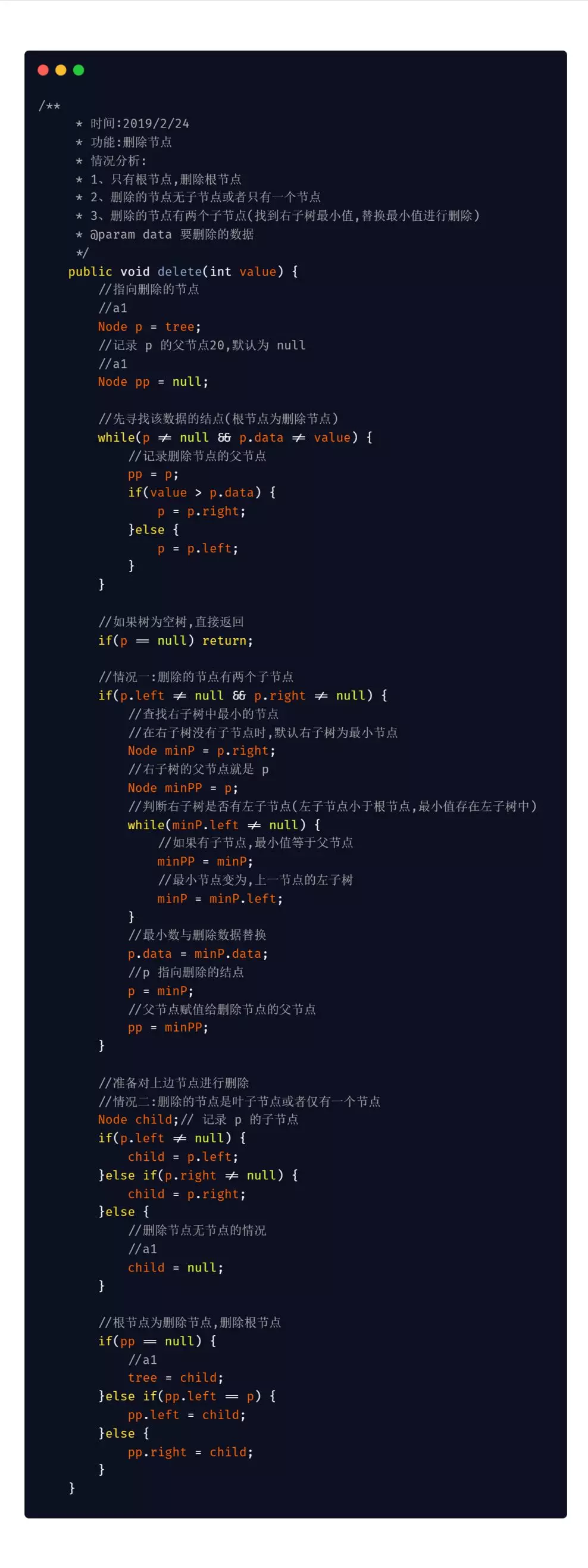
Java 版本
通过上边二叉树的三种操作,我们做一个总结,为什么各种操作的不相同,都是朝着什么方向去变化的?对了,无论是插入还是查找、删除,都是能够让二叉查找树变化后的结构还能够具备二叉查找树的特点(左子节点小于根节点,右子节点大于根节点)。
5、重复数据怎么办?
以上我们存储的只是不重复的数据,如果我们数据中有重复数据怎么进行操作呢?
我们有以下几种方式进行优化,我们可以用数组和链表等动态的数据结构充当节点,这样就可以把重复的数据存储到一个节点上。
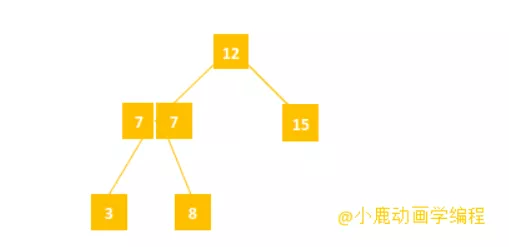
还有一种策略就是我们把重复的数据当做大于根节点处理,也就是存储到右子树上。
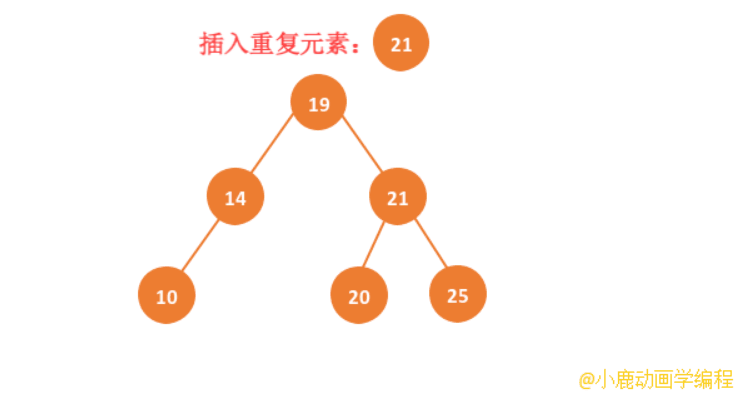
但是我们的查找和删除要优化下,如果查找一个元素,查找到了,但是需要继续往下查找,因为可能存在重复的数据。删除也是同样的道理,删除一个元素,删除之后继续查找是否还存在重复数据,然后对其重复数据进行删除。
6、二叉查找树的性能
上边我们分别对二叉查找树的插入、删除、查找的时间效率进行了分析,也说了时间效率和树的高度成正比,那么问题来了,树的高度如何求?
我们运用我们的数学功底算一下,我们先算算一颗完全二叉树有多少的节点,第一层有1个,第二层2个,第三层,4 个,依次类推,第 n 层有多少就要用到等比数列,也就是 2 的n-1次方。
我们粗略估算,让等式等于 1 时,此时n = log2n+1,此时我们的 n 代表是树的第几层,然后转化为高度就是h = log2n。
上边我们已经分析过,二叉查找树的无论是插入还是查找、删除,都与树的高度成正比,也就是log2n。
但是我们要记住一个前提,我们前边分析的树的高度是完全二叉树,如果不是完全二叉树,那么时间复杂度就会发生改变,比如我们一直插入的数据会导致整棵树会失去平衡,退化成链表,时间复杂度就变成了O(n)。
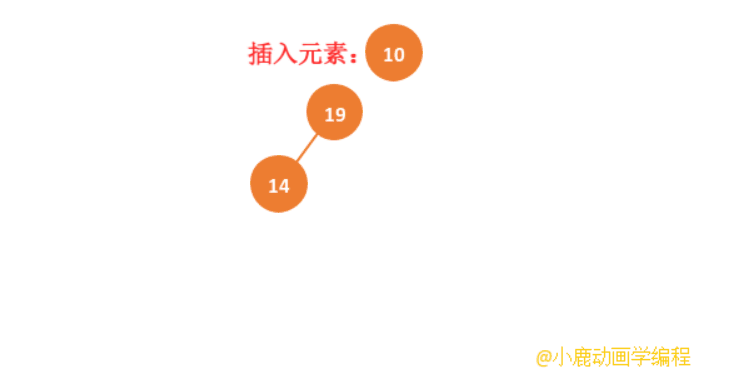
那么如何解决上边的问题呢?我们需要构建一棵平衡的二叉查找树,每当节点之间快要失去平衡的时候,经过一定的策略,使其达到平衡的状态,这样就算在最坏的情况下也不会退化成链表。比如,AVL 树、红黑树,这些涉及到的比较难,我们本篇不深入了解。
7、小结
今天我们主要讲了二叉树中的一种特殊二叉树,二叉查找树又叫做二叉搜索树。
二叉查找树是根据自身的特点,左子节点小于根节点,右子节点大于根节点。从而达到能够实现动态的插入、删除、查找操作,且操作的时间复杂度和树的高度成正比。但是如果一直不平衡的插入,会导致出现二叉查找树退化成链表的情况,所以我们更需要一种平衡的二叉查找树。
❤️ 不要忘记留下你学习的脚印 [点赞 + 收藏 + 评论]
文章+动画写了好几个小时,不妨点赞支持一下。嘻嘻,你不点赞说明你很自私,你怕那么好的文章让别人也看到。开个小小玩笑。
可以关注小鹿公众号:「小鹿动画学编程」,后台回复:“资源”。送你一份小鹿之前自学的资料和拉你进免费学习群哦!
作者Info:
【作者】:小鹿
【原创公众号】:小鹿动画学编程。
【简介】:和小鹿同学一起用动画的方式从零基础学编程,将 Web前端领域、数据结构与算法、网络原理等通俗易懂的呈献给小伙伴。先定个小目标,原创 1000 篇的动画技术文章,和各位小伙伴共同努力一起学习!公众号回复 “资料” 送一从零自学资料大礼包!
【转载说明】:转载请说明出处,谢谢合作!~