无处不在的前端矩阵变换

前端论道
7,125 阅读7分钟

在前端开发中不论CSS3也好，SVG也好，还是Canvas，无论多复杂的图形，都是由一个个点组成的。一个元素渲染后就可以得到一张位图，然后对这个位图上每一点进行变换，就可以得到新的一张位图，从而产生了视觉上的平移translate、旋转rotate、缩放scale、拉伸skew 等效果。这一切都是变换矩阵的功劳。

2d与3d矩阵变换公式

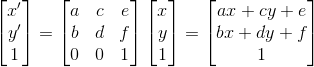
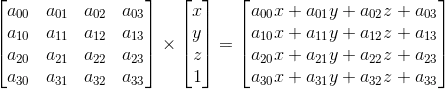
CSS3中的2d矩阵变换

  • CSS3中的 transform: translate(tx, ty) 等价于 transform: matrix(1,0,0,1,tx,ty)

  • CSS3中的 transform:rotate(θ) 等价于 transform: matrix(cosθ,sinθ,-sinθ,cosθ,0,0)

  • CSS3中的 transform: scale(Sx, Sy) 等价于 transform: matrix(Sx,0,0,Sy,0,0)

  • CSS 3中的 transform: skew(θx,θy) 等价于 transform:matrix(tan(θx),0,0,tan(θy),0,0)

CSS3中的3d矩阵变换

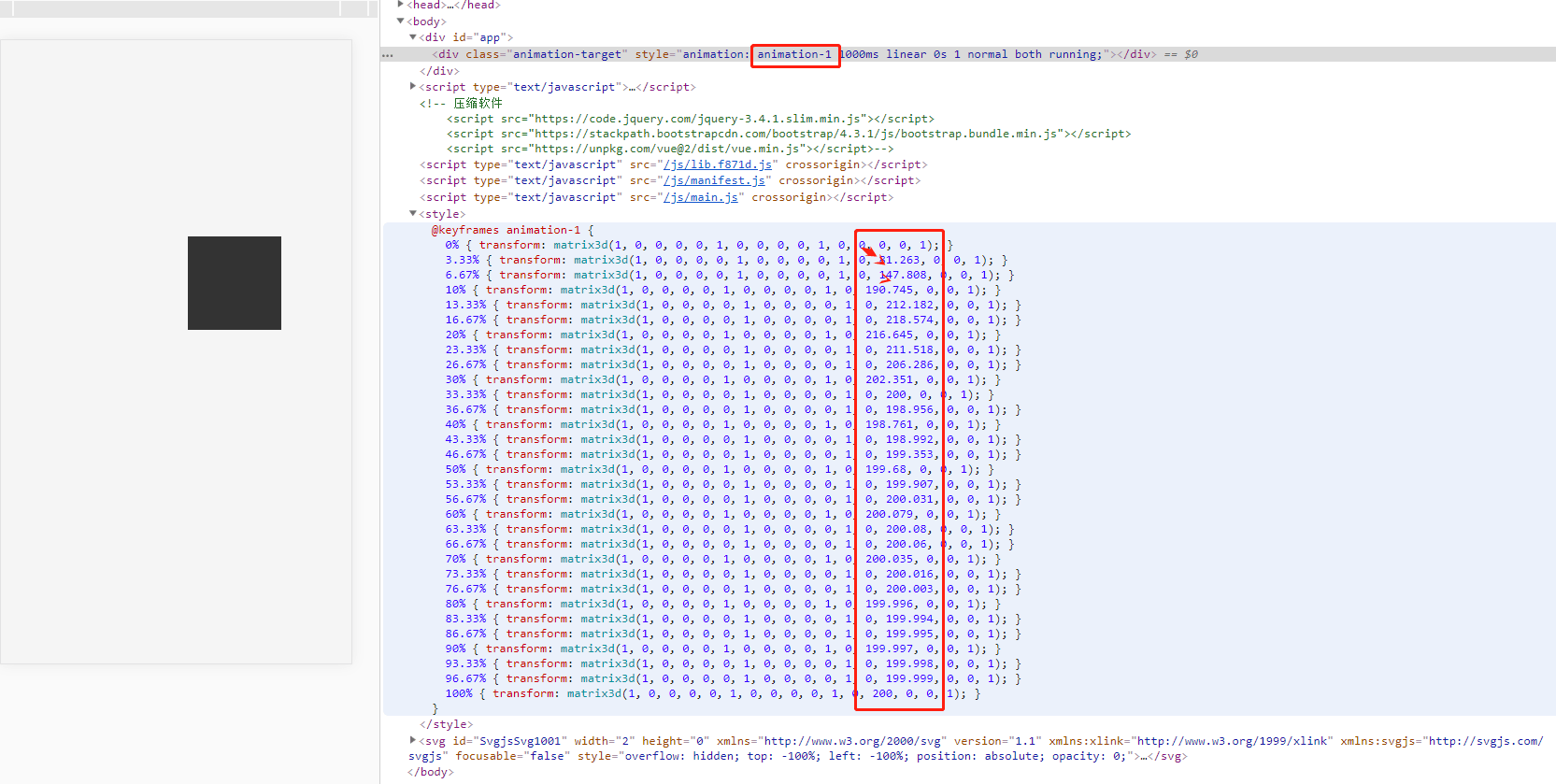
给个简单的demo，利用CSS3动画库 bounce.js 通过设置元素属性 transform:matrix3d (1-16位参数值) 让元素偏移 200px。 从matrix三阶矩阵到matrix3d四阶矩阵，本质上很多东西都与2D大同小异，只是复杂度不一样而已。

<!--dom-->
<div class="animation-target"></div>

<!--css代码-->
.animation-target {
  background-color: #333;
  height: 100px;
  width: 100px;
}

<!--js代码-->
let bounce = new Bounce();
bounce.translate({
  from: { x: 0 },
  to: { x: 200 }
})
bounce.applyTo(document.querySelector('.animation-target'))

/*
   bounce.js 其余scale、rotate、skew等api最终都是通过transform:matrix3d(1-16位参数值)来实现元素的动画效果
*/

效果图如下：matrix3d对应的矩阵运算细节可参考 bounce.js

svg中的矩阵变换

svg中的变换原理和css3中的类似，但是在svg中没有相关的属性来设置变换的中心点，只能通过translate来模拟。如下设置transform-origin是不生效的

<!--dom-->
<svg xmlns="http://www.w3.org/2000/svg" version="1.1" width="100" height="190">
   <rect id="SvgjsRect1008" width="100" height="100" transform-origin="0% 0%" transform="translate(100, 0)"></rect>
</svg>

/*
   transform-origin="0% 0%" 设置是不生效的
*/

下面结合SVG.js 这个开源库来看下svg中的矩阵变换应用

<!--dom 作为SVG.js的挂载节点-->
<div id="drawing"></div>

<!--js-->
let draw = SVG('drawing').size(300, 300)
let rect = draw.rect(100, 100)
rect.rotate(45)  // 旋转45度

如图：

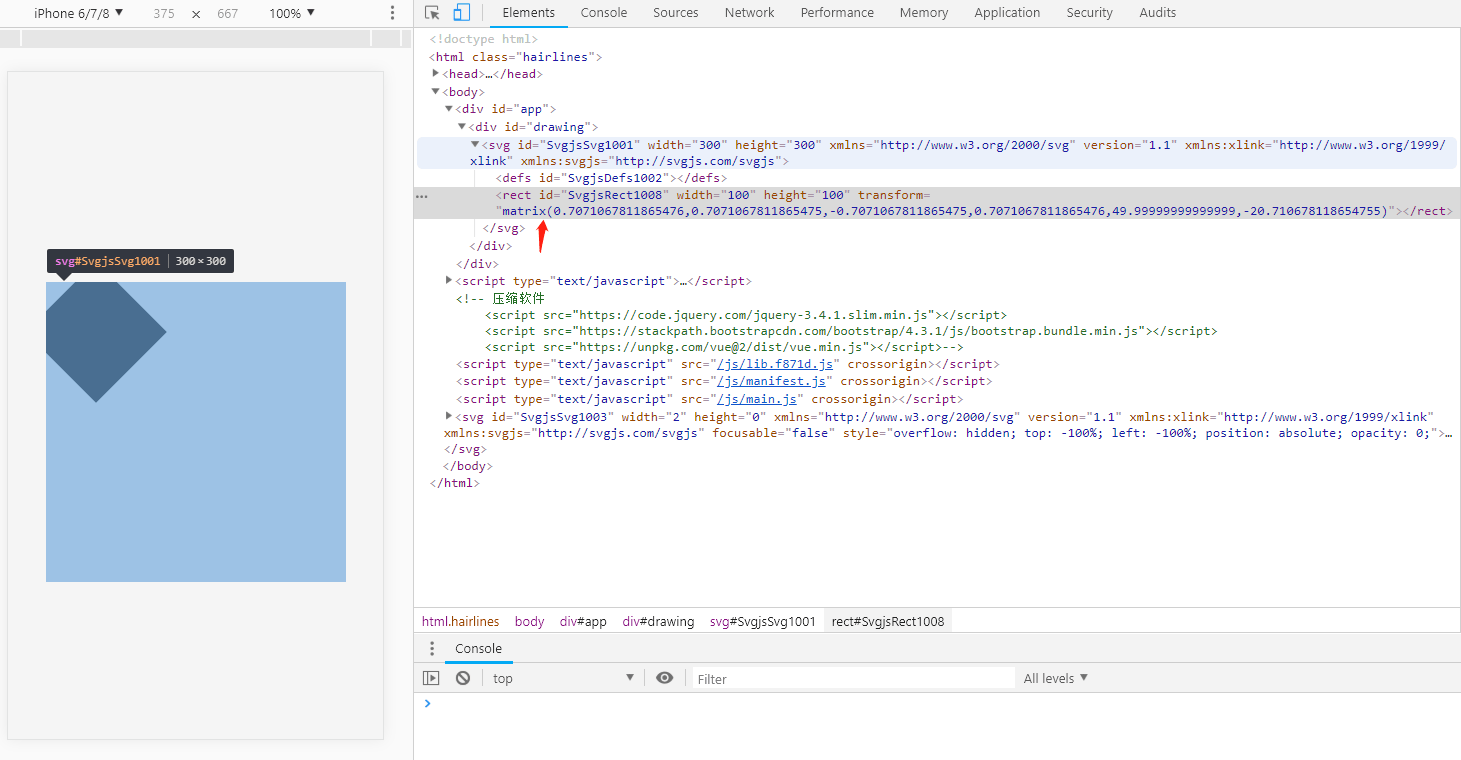
那么rect.rotate(45) 是怎么变成 上图中的 matrix 的呢？ 如下：

<!--SVG.js 中的关键代码截取-->
rect.rotate(45)
=>
rotate: function(d, cx, cy) {
 return this.transform({ rotation: d, cx: cx, cy: cy })
}
transform: function(o, relative) {
 var target = this, matrix; // this 通过SVG.js new 出的一个react实例对象 
 matrix = new SVG.Matrix(target) // 获取当前元素的transform: matrix矩阵值,具体实现可以查阅SVG.js源码
 ... 此处省略部分代码
 ensureCentre(o, target)  // 通过svg原生api, element.node.getBBox()来计算元素的中心点o
  // 应用矩阵
  matrix = relative ? 
    // relative
    matrix.rotate(o.rotation, o.cx, o.cy) :
    // absolute
    matrix.rotate(o.rotation - matrix.extract().rotation, o.cx, o.cy)
}
rotate: function(r, cx, cy) {
  // convert degrees to radians
  r = SVG.utils.radians(r)
  // 计算对应的旋转矩阵, 对应a,b,c,d,e,f值如下
  return this.around(cx, cy, new SVG.Matrix(Math.cos(r), Math.sin(r), -Math.sin(r), Math.cos(r), 0, 0))
}
// Transform around a center point 以中心点来进行旋转
around: function(cx, cy, matrix) {
 //这里很重要：svg以某个参考点变换时 => 通过先平移translate(cx,cy), 然后transform目标matrix值, 再进行反平移translate(-cx,-cy)
 return this
   .multiply(new SVG.Matrix(1, 0, 0, 1, cx || 0, cy || 0))
   .multiply(matrix)
   .multiply(new SVG.Matrix(1, 0, 0, 1, -cx || 0, -cy || 0))
}
multiply: function(matrix) {
  // 这里是把元素当前的transform: matrix属性值与目标矩阵相乘
  return new SVG.Matrix(this.native().multiply(parseMatrix(matrix).native()))
}
native: function() { 
  // SVG.js 中的矩阵相乘, 利用的是svg元素的原生api, createSVGMatrix()来实现
  // create new matrix
  var matrix = SVG.parser.native.createSVGMatrix()

  // update with current values
  for (var i = abcdef.length - 1; i >= 0; i--)
    matrix[abcdef[i]] = this[abcdef[i]]

  return matrix
}

//最后把最终计算的matrix变换值设置到react元素上就完成了
this.attr('transform', matrix)

canvas中的矩阵变换

同样结合一个canvas开源库 fabric.js 来说下canvas中的矩阵变换应用，这个库实现很牛叉，里面有大量的功能点，比如: 通过 canvas 绘制的元素如何解决Retina 屏中元素模糊的问题，以及如何采用离线canvas做性能提升等等。

<!--dom 作为canvas绘制画布-->
<div id="drawing"></div>

<!--js-->
let canvas = new fabric.Canvas('canvas', { width: "375", height: "500" })
let react = new fabric.Rect({ width: 100, height: 100, left: 100, top: 100, fill: 'red', angle: 10 })
canvas.add(react)

如图：

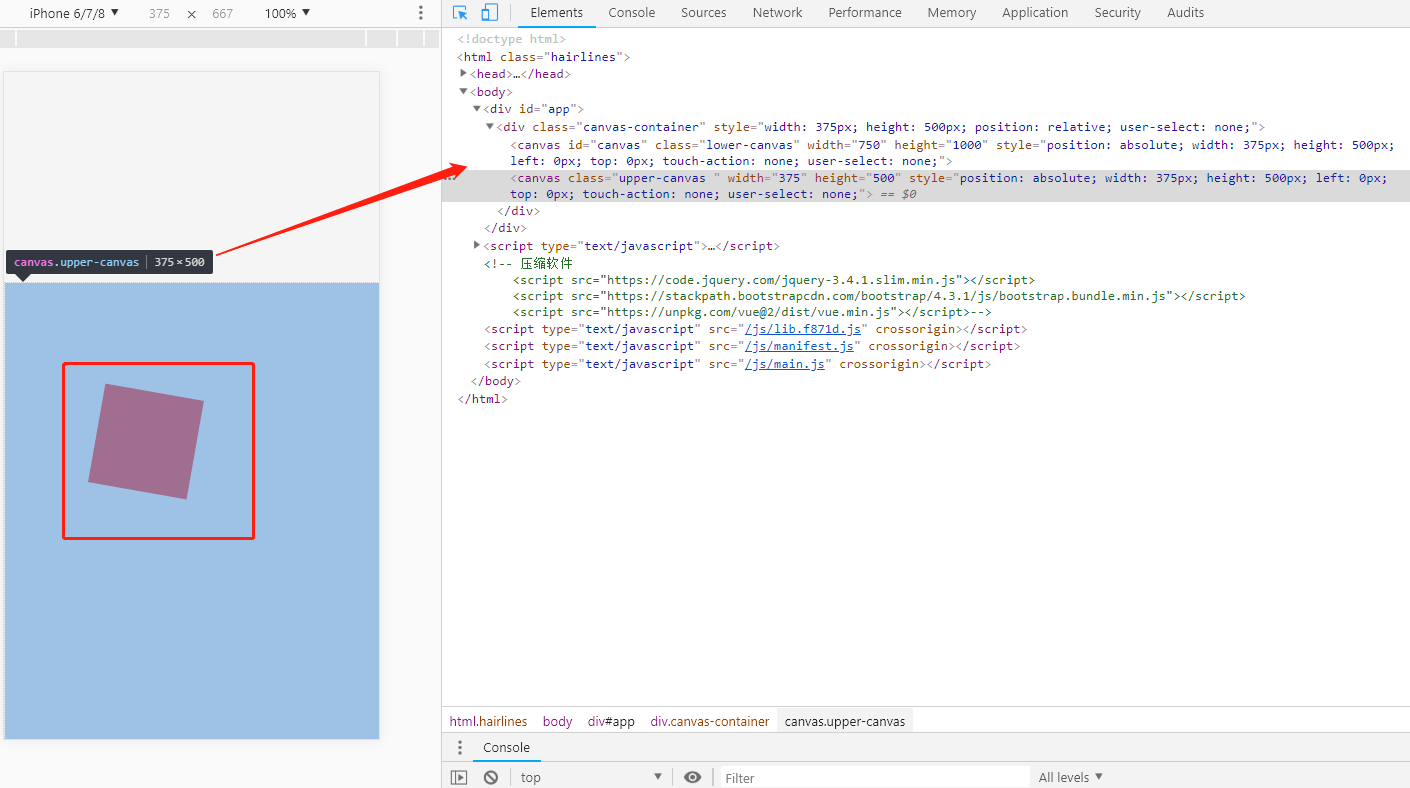
同样说下fabric.js 是如何绘制的

<!-- fabric.js 部分代码截取，有大量的代码省略，只挑取关键流程代码 -->
canvas.add(react)
=>
add: function () {
  /* 变量说明：
    this => new fabric.Canvas 实例对象
  */
  this.renderOnAddRemove && this.requestRenderAll(); 
  return this; 
},
// ...省略部分代码...
renderAll: function () {
  /* 变量说明：
    this => new fabric.Canvas 实例对象
    this.contextContainer => 如上图class="lower-canvas" canvas元素的2d绘图上下文
    this._chooseObjectsToRender() => 获取要渲染的object对象，这里就是react实例对象
  */
  var canvasToDrawOn = this.contextContainer;
  this.renderCanvas(canvasToDrawOn, this._chooseObjectsToRender()); 
  return this;
},
renderCanvas: function(ctx, objects) {
  /* 变量说明：
    this => new fabric.Canvas 实例对象
    ctx => 如上图class="lower-canvas" canvas元素的2d绘图上下文
    objects =>  fabric.js 创建的react实例对象
  */
  // 擦除lower-canvas
  this.clearContext(ctx);  
  ctx.save();
  // 对object元素进行绘制draw
  this._renderObjects(ctx, objects);
  ctx.restore();
},
// ...省略部分代码，最终调用object的render方法，如下 ...
render: function(ctx) {
  /* 变量说明：
    this => fabric.js 创建的react实例对象
    ctx => 如上图class="lower-canvas" canvas元素的2d绘图上下文
  */
  ctx.save();  
  // 对ctx坐标进行变换 很重要 
  this.transform(ctx);
  // 如果元素需要走缓存策略：则会创建缓存canvas, 然后在缓存canvas上绘制object对象(这里是fabric.js 创建的react实例对象)，最后再把缓存canvas => ctx.drawImage(this._cacheCanvas, -this.cacheTranslationX, -this.cacheTranslationY); 绘制到lower-canvas上
  if (this.shouldCache()) {
    // 创建了一个缓存canvas、并在缓存canvas上draw绘制object元素
    this.renderCache();
    // 然后将缓存的canvas绘制到lower-canvas中
    this.drawCacheOnCanvas(ctx);
  }
  else {
    this._removeCacheCanvas();
    this.drawObject(ctx);
  }
  ctx.restore();
  // ...省略部分代码...
},
// 接下来主要看 this.transform(ctx); 对lower-canvas的坐标变换
transform: function(ctx) {
  var m;
  if (this.group && !this.group._transformDone) {
    m = this.calcTransformMatrix();
  }
  else {
    // 根据object的信息, 计算矩阵
    m = this.calcOwnMatrix();
  }
  // 将lower-canvas坐标系平移到
  ctx.transform(m[0], m[1], m[2], m[3], m[4], m[5]);
},
calcOwnMatrix: function() {
  // ...省略部分代码...
  /* 变量说明：
    this => fabric.js 创建的react实例对象，也即是object
  */
  var tMatrix = this._calcTranslateMatrix();
  this.translateX = tMatrix[4];
  this.translateY = tMatrix[5];
  cache.key = key;
  cache.value = fabric.util.composeMatrix(this);
  return cache.value;
},

..........  下面这部分是计算object经过scale、rotate等后的中心点坐标 ....................
_calcTranslateMatrix: function() {
  var center = this.getCenterPoint();
  return [1, 0, 0, 1, center.x, center.y];
},
getCenterPoint: function() {
  var leftTop = new fabric.Point(this.left, this.top);
  // 这里的 this.originX, this.originY就是rotate的旋转参考点
  return this.translateToCenterPoint(leftTop, this.originX, this.originY);
},
translateToCenterPoint: function(point, originX, originY) {
  // 根据this.originX, this.originY 计算object中心点center
  var p = this.translateToGivenOrigin(point, originX, originY, 'center', 'center');
  // 计算得到的center点后，再计算旋转后的点坐标
  if (this.angle) {
    return fabric.util.rotatePoint(p, point, degreesToRadians(this.angle));
  }
  return p;
},
rotatePoint: function(point, origin, radians) {
  // 这里计算旋转后的坐标，先减去旋转参考点this.originX, this.originY 的值，然后将得到的值经过旋转radians角度后，再将得到的坐标加上参考点this.originX, this.originY的值，既可得到最终的坐标值
  point.subtractEquals(origin);
  var v = fabric.util.rotateVector(point, radians);
  return new fabric.Point(v.x, v.y).addEquals(origin);
},
rotateVector: function(vector, radians) {
  var sin = fabric.util.sin(radians),
      cos = fabric.util.cos(radians),
      rx = vector.x * cos - vector.y * sin,
      ry = vector.x * sin + vector.y * cos;
  return {
    x: rx,
    y: ry
  };
},

..........  下面这段是对 fabric.util.composeMatrix(this) 说明....................
composeMatrix: function(options) {
  /* 变量说明：
    options => fabric.js 创建的react实例对象，也即是object
  */
  // 平移中心点的矩阵
  var matrix = [1, 0, 0, 1, options.translateX || 0, options.translateY || 0],
      multiply = fabric.util.multiplyTransformMatrices;
  // 平移中心点的矩阵 * 旋转对应的矩阵
  if (options.angle) {
    matrix = multiply(matrix, fabric.util.calcRotateMatrix(options));
  }
  // 平移中心点的矩阵 * 旋转对应的矩阵 * 缩放及拉伸的矩阵
  if (options.scaleX || options.scaleY || options.skewX || options.skewY || options.flipX || options.flipY) {
    matrix = multiply(matrix, fabric.util.calcDimensionsMatrix(options));
  }
  return matrix;
},
// 3*3 的矩阵相乘
multiplyTransformMatrices: function(a, b, is2x2) {
  // Matrix multiply a * b
  return [
    a[0] * b[0] + a[2] * b[1],
    a[1] * b[0] + a[3] * b[1],
    a[0] * b[2] + a[2] * b[3],
    a[1] * b[2] + a[3] * b[3],
    is2x2 ? 0 : a[0] * b[4] + a[2] * b[5] + a[4],
    is2x2 ? 0 : a[1] * b[4] + a[3] * b[5] + a[5]
  ];
},
// 计算旋转的矩阵坐标
calcRotateMatrix: function(options) {
  if (!options.angle) {
    return fabric.iMatrix.concat();
  }
  var theta = fabric.util.degreesToRadians(options.angle),
      cos = fabric.util.cos(theta),
      sin = fabric.util.sin(theta);
  return [cos, sin, -sin, cos, 0, 0];
},
// 计算缩放和拉伸的矩阵坐标
calcDimensionsMatrix: function(options) {
  var scaleX = typeof options.scaleX === 'undefined' ? 1 : options.scaleX,
      scaleY = typeof options.scaleY === 'undefined' ? 1 : options.scaleY,
      scaleMatrix = [
        options.flipX ? -scaleX : scaleX,
        0,
        0,
        options.flipY ? -scaleY : scaleY,
        0,
        0],
      multiply = fabric.util.multiplyTransformMatrices,
      degreesToRadians = fabric.util.degreesToRadians;
  if (options.skewX) {
    scaleMatrix = multiply(
      scaleMatrix,
      [1, 0, Math.tan(degreesToRadians(options.skewX)), 1],
      true);
  }
  if (options.skewY) {
    scaleMatrix = multiply(
      scaleMatrix,
      [1, Math.tan(degreesToRadians(options.skewY)), 0, 1],
      true);
  }
  return scaleMatrix;
},

// 最后将经过平移中心点坐标矩阵 * 旋转对应的矩阵 * 缩放及拉伸的矩阵计算得到的matrix值设置到lower-canvas坐标系中, 如上transform方法所示
ctx.transform(m[0], m[1], m[2], m[3], m[4], m[5]);

//接下来进行元素的绘制, 上面render方法中由于篇幅的原因绘制过程就不展开了
...

到这里终于把fabric.js 绘制元素过程中坐标矩阵的变换说完了，具体的代码细节自行查阅源码吧！

最后

了解矩阵变换的概念，旨在揭开相关开源代码实现的背后细节，欢迎吐槽！

关注我们

avatar
文章
阅读
粉丝
相关推荐
使用react-konva制作在线photoshop(2)——字体的文本与样式的修改
2.5k阅读
 · 
2点赞
konva中如何实现这种效果呢
570阅读
 · 
0点赞
React Fabric.js 实现可拖拽旋转的线形
649阅读
 · 
1点赞
【理论】canvas之绘制圆角矩形的方式
4.0k阅读
 · 
1点赞
图形编辑器：图形和辅助线绘制的坐标问题
1.7k阅读
 · 
2点赞
pixi.js7.1.4开发微信小游戏环境搭建详细教程
969阅读
 · 
4点赞
Fabric Js 绘图工具使用感
322阅读
 · 
1点赞
konva系列教程2：绘制图形
990阅读
 · 
2点赞
基于fabricjs搭建canvas画布 - 画笔、橡皮擦
384阅读
 · 
3点赞

友情链接：