插入排序(Insertion Sort)
插入排序,非常类似于扑克牌的排序,相信各位读者,都有玩过扑克牌,如逢年过节可能会和亲朋好友一起斗地主,当我们拿到牌以后,一般都会对牌进行排序,这样会比较方便出牌。例如现在手里有2,4,5,104张牌,当摸到一张7的时候,就会把7插入下图中的位置。将7插入合适的位置后,保证原来的序列有序,这就叫做插入排序。

插入排序的执行流程
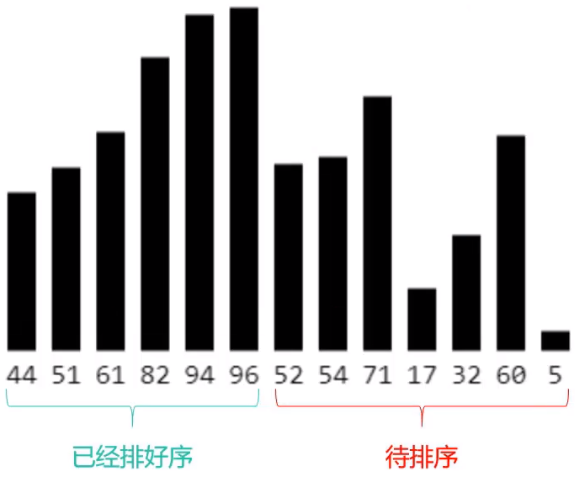
- 在执行过程中,插入排序会将序列分为2部分;例如下图的这一堆数据属于待排序数据
- 从头开始扫描每一个元素
- 每当扫描到一个元素,就将它插入到头部合适的位置,使得头部依然保持有序
最终,可以实现的代码如下
protected void sort() {
for (int begin = 1; begin < array.length; begin++) {
int cur = begin;
while (cur >0 && cmp(cur,cur - 1) < 0) {
swap(cur,cur - 1);
cur--;
}
}
}
现在将插入排序与前面的几种排序算法进行堆10000个数据排序比较,可以发现排序结果是没有问题的,并得到的结果是

从目前来看,插入排序的性能和选择排序的性能差不多。接下来,看一下插入排序的另外一个概念。
逆序对(Inversion)
什么是逆序对?
如果是正序的话,前面元素只小,如果是逆序的话,则前面的元素值更大,所以现在有如下数组<2,3,8,6,1>,可以组成这5对逆序对<2,1>,<3,1>,<8,1>,<8,6>,<6,1>
如果某个数组,组成的逆序对为0,那么该数组中元素肯定是升序的,所以如果逆序对多的话,会进行的交换次数多,所以插入排序的时间复杂度与逆序对的数量成正比
逆序对的数量越多,插入排序的时间复杂度越高
为什么呢?假设现在有如下的一堆元素

可以发现,当前这些元素,可以组成的逆序对数量达到最大,为什么逆序对这么高的一堆元素,会导致插入排序的效率是最低的,时间复杂度是最高的呢?
当现在对元素8进行排序,则9,8需要交换位置,得到下面的结果

重复依次排序,最终的结果为
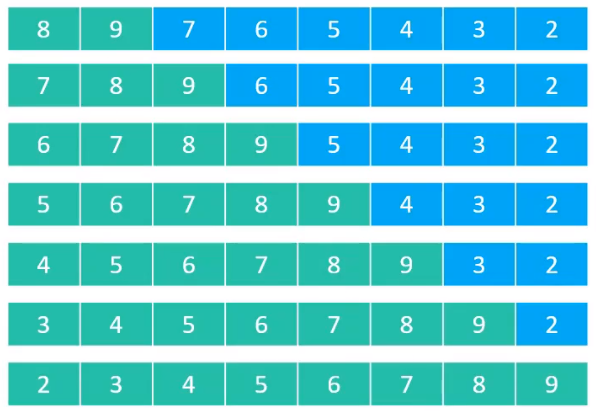
通过观察可以发现,当新拿到一个待排序的元素时,该元素总是要被插入到最前面,这样需要做的交换操作是最多的,并且以现在的算法的话,是一个一个的比较进行交换的,所以像这种情况,时间复杂度肯定是最高的。
所以插入排序有以下的结论
- 最坏,平均时间复杂度为:O(n^2)
- 最好时间复杂度为:O(n)【没有逆序对的时候】
- 空间复杂度:O(1)
- 属于稳定排序
当逆序对的数量极少时,插入排序的效率特别高,甚至速度比O(nlogn)级别的快速排序还要快
数据量不是特别大的时候,插入排序的效率也是非常好的
优化
由于发现现在的代码中,比较后都需要进行交换,并且不一定一次就能交换到最期望的位置,所以可以想想,是否能将交换转为挪动呢?是可以的。操作步骤如下
- 先将待插入的元素备份;例如现在需要将下图中的下标尾5的元素插入到合适的位置,这个时候,先将该元素内容进行备份
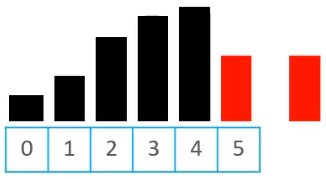
- 头部有序数据中比待插入元素大的,都往尾部方向挪动一个位置
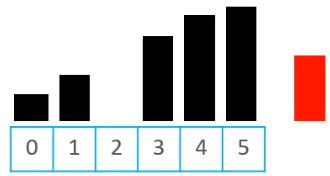
- 将待插入的元素,放到最终合适的位置
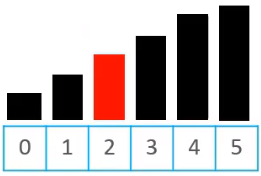
为什么这种就可以优化呢?如果按照以前的思路,交换一对元素,需要3行代码才能实现,但是现在挪动一个元素,只需要一行代码就实现了。所以优化后的代码为
protected void sort() {
for (int begin = 1; begin < array.length; begin++) {
int cur = begin;
E element = array[cur];
while (cur >0 && cmp(element,array[cur - 1]) < 0) {
array[cur] = array[cur - 1];
cur--;
}
array[cur] = element;
}
}
通过优化后,对比前面的排序算法,得到的结果为【注:InsertionSort2为优化后,InsertionSort1为优化前】

并且,由于现在是对while循环中的代码进行优化,所以进入while循环次数越多的话,优化会更明显。不过现在的插入排序,还可以进一步优化,在了解如何进一步优化之前,需要了解另外一个知识。二分搜索(Binary Search)
二分搜索(Binary Search)
说到二分搜索,你可能会马上想起一个东西,就是二叉搜索树,如果还不了解二叉搜索树,可以点击这里,有专门的文章进行介绍。是的,二叉搜索树的思想和这里的二分搜索是很相似的,那二分搜索有什么用呢?那可以先来思考下面一个问题
如何确定一个元素在数组中的位置?(假设数组里面全部都是整数)
- 如果是下图中的这种无序数组,可以从第0个位置开始遍历搜索,平均时间复杂度为:O(n)

- 如果数组是下图中的有序数组,则可以使用二分搜索,其最坏时间复杂度为:O(logn)

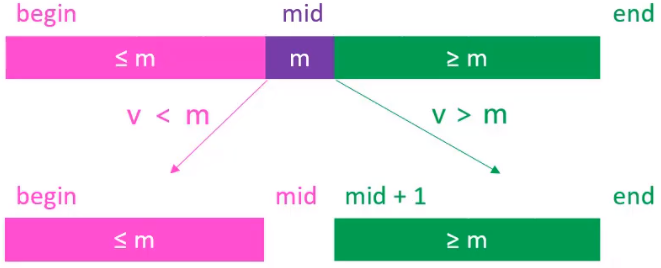
那二分搜索,具体是怎么去工作的呢?现在通过一个下图来统一表示二分搜索

- 图片中线条长度表示数组长度
- m表示中间的元素,其下标尾mid
- 所以m左边部分的元素大小都是≤m的
- m右边部分的元素大小都是≥m的
- begin表示最前面元素的索引
- end表示最尾部元素的索引+1
所以,对于任何一个有序的数组,都可以通过上图中的方式来进行表达。
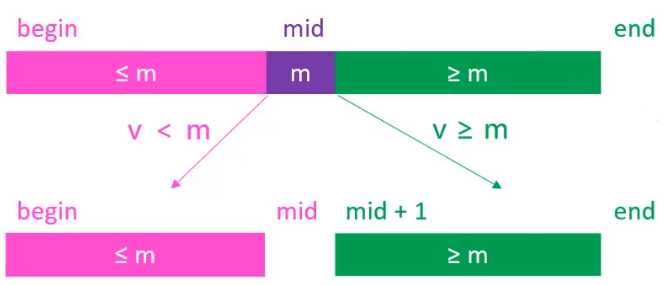
假设在[begin,end)范围内搜索某个元素v,可以让mid == (begin + end) / 2
- 如果mid位置对应的元素m,是v<m的,则去mid的左边继续搜索,这时的搜索范围变为了[begin,mid)之间
- 如果mid位置对应的元素m,是v>m的,则去mid的右边继续搜索,这时的搜索范围变为了[mid +1,end)之间
- 如果mid位置对应的元素m,是v == m,则直接返回mid
通过这种方式,就可以直接获取到元素v对应的索引
二分搜索实际应用
应用一:元素存在
假设现在要从下图数组中搜索元素10,则是先找计算中间元素的位置,(0 + 7) / 2 = 3,得到中间位置的元素8
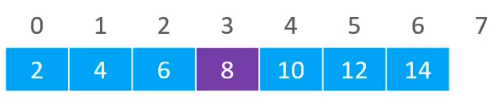
发现,要搜索的元素10的值是大于8的,所以现在就开始从8的右边开始查找元素。再利用(4 + 7) / 2 = 5,所以就得到了索引为5的元素,其值为12。
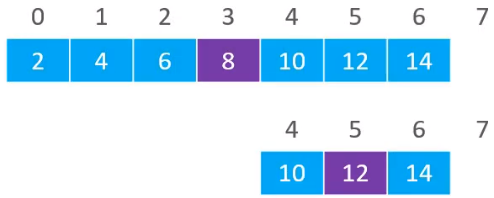
发现要搜索的元素10的值是比12小的,所以就开始从剩下元素中的左边进行查找,最终剩下的范围就变为了[4,5),然后再利用 (4 + 5) / 2 = 4,最终发现值与要搜索的元素相等,就可以直接返回搜索到的下标
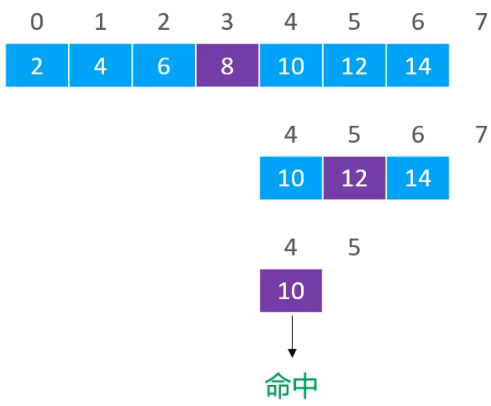
应用二:元素不存在
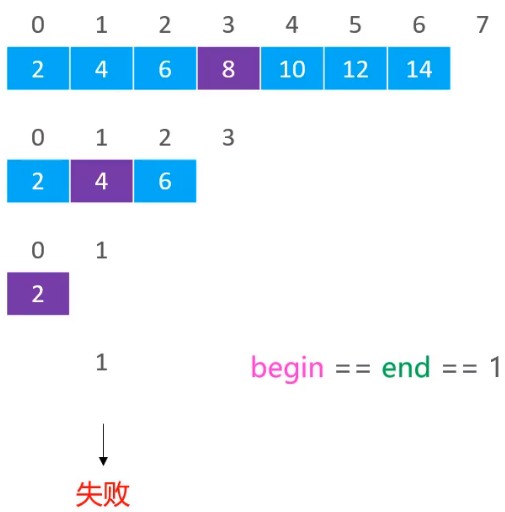
假设现在要从下面的数组中搜索元素3,同样是先找计算中间元素的位置,(0 + 7) / 2 = 3,得到中间位置的元素8

发现要搜索的元素3的值是小于中间元素8,则开始从8的左边继续搜索,再利用(0 + 3) / 2 = 1,得到中间位置的索引为1,其值为4
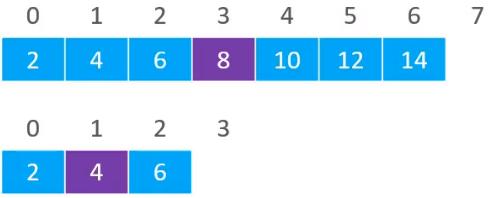
通过比较,发现4是大于要搜索的元素3,即继续在4的左边进行搜索,计算索引(0 + 1)/ 2 = 0,得到索引为0的元素为2
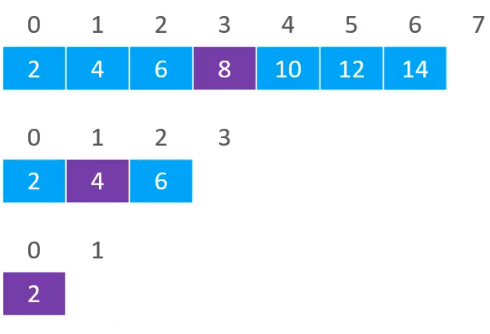
继续比较,发现元素2的值是小于要搜索的元素3的,所以继续在(1,1)范围内搜索。由于(1,1)范围是不合理的,所以最终搜索失败
根据上面的流程,可以转换为下面的代码
public static int indexOf(int[] array, int v) {
if (array == null || array.length == 0) return -1;
int begin = 0;
int end = array.length;
while (begin < end) {
int mid = (begin + end) >> 1;
if (v < array[mid]) {
end = mid;
} else if (v > array[mid]) {
begin = mid + 1;
} else {
return mid;
}
}
return -1;
}
代码实现以后,现在思考一个问题,如果存在多个重复的值,最终会返回哪一个?
这种情况下,最终会返回哪一个元素,是不确定的。所以这一点需要注意。
好的。了解了二分搜索以后,现在可以继续优化插入排序了。
优化-二分搜索
结合二分搜索,在插入排序时,可以先利用二分搜索出合适的插入位置,然后再将元素v插入。
由于上面实现的二分搜索,如果找不到时,是返回-1,这样是不可行的。所以在插入排序时,还需要继续改进二分搜索
同样的,假设是在[begin,end)范围内搜索某个元素v,mid == (begin + end) / 2

这一次的搜索和前面的二分搜索,是有一点不一样的
如果v < m,去[begin,mid)范围内二分搜索
如果v ≥m,去右边的部分中去查找
插入位置实例分析
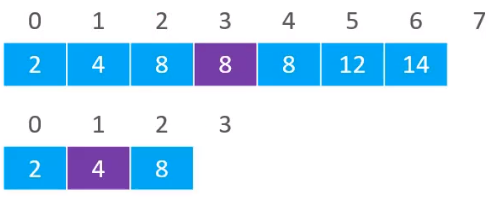
现在要从下列的数组中插入元素5,可以计算从中间位置为3,对应的元素是8

通过比较,5是小于搜索出来的元素的,所以在[0,3)位置继承查找,计算出中间位置为1,对应的元素为4
又通过比较,发现5大于搜索出来的4,所以在[2,3)位置继承查找,计算出中间元素的位置为2,对应的元素为8
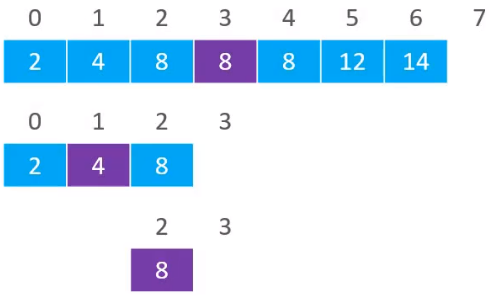
通过比较,发现5是小于8的。则往左边找,但是现在的搜索范围为[2,2),即begin == end,是不合理的。但是恰巧,begin == end的位置就是要插入的位置。
所以结合插入排序,对二分搜索进行改进后的结果为
public static int search(int[] array,int v) {
if (array == null || array.length == 0) return -1;
int begin = 0;
int end = array.length;
while (begin < end) {
int mid = (begin + end) >> 1;
if (v < array[mid]) {
end = mid;
} else {
begin = mid + 1;
}
}
return begin;
}
利用改进后的思路,对插入排序进行优化后为
protected void sort() {
for (int begin = 1; begin < array.length; begin++) {
int insertIndex = search(begin);
E v = array[begin];
for (int i = begin; i > insertIndex; i--) {
array[i] = array[i - 1];
}
array[insertIndex] = v;
}
}
private int search(int index) {
if (array == null || array.length == 0) return -1;
int begin = 0;
int end = index;
while (begin < end) {
int mid = (begin + end) >> 1;
if (cmp(array[index],array[mid]) < 0) {
end = mid;
} else {
begin = mid + 1;
}
}
return begin;
}
利用该优化,新建了一个InsertionSort3类,利用该类与前面的几种算法进行比较。结果如下

可以看到,优化后的性能进一步得到了提升,并且比较的次数极少。所以InsertionSort3相对于InsertionSort2来讲,优化的地方在较少了比较次数。
经过优化后,效率得到了提升,不过需要注意,使用二分搜索,只是减少了比较次数,但是插入排序的平均时间复杂度依然是O(n^2)
完!