Dijkstra
Dijkstra属于单源最短路径算法,用于计算一个顶点到其他所有顶点的最短路径。
- 使用前提:不能有负权边。也就是说,如果图中有负权边,不能使用Dijkstra算法来计算最短路径,但是可以使用Bellman-Ford来计算
- 时间复杂度:可优化至O(ElogV),E是边的数量,V是顶点数量。
Dijkstra算法是由荷兰科学家Edsger Wybe Dijkstra发明的,也曾在1972年获得图灵奖。


Dijkstra等价思考
现在就来研究一下,Dijkstra算法是怎样的。
首先,Dijkstra的原理其实和生活中的一些自然现象是完全一样的。什么自然现象呢?接下来就一起跟着下面的描述,来想想一件事情。如果想清楚的话,对于理解Dijkstra算法会大有帮助。
- 把图中的没一个顶点都想象成为一块小石头。
- 每一条边想象成是一条绳子,每一条绳子都连接着2块小石头,边的权值就是绳子的长度。
- 将小石头和绳子平放在一张桌子上,(下图是一张俯视图,图中黄颜色的是桌子)
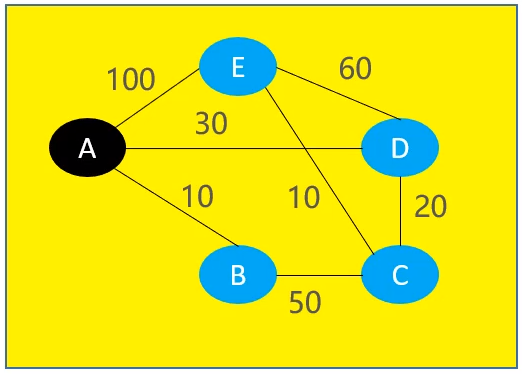

- 接下来想象以下,用手拽着小石头A,慢慢地向上提起来,远离桌面,如下图所示的侧视图
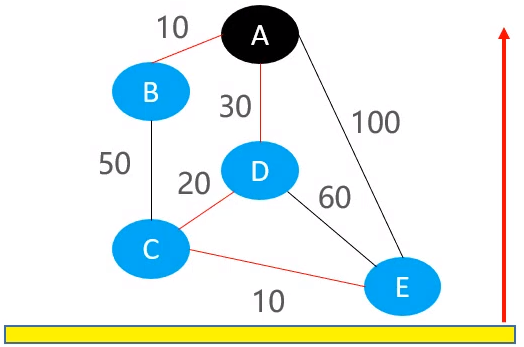
- 离开桌面的顺序取决于其余顶点距离顶点A的最短绳子长度,也就是最短路径。所以,最终你会发现,B,D,C,E会依次离开桌面,当所有石头都离开桌面时,有的绳子会蹦直,而有的绳子是松的。
- 最后绷直的绳子就是A到其他小石头的最短路径。
关键信息:后离开桌面的小石头,都是被先离开桌面的小石头拉起来的。
在本节中,讨论的Dijkstra算法与这种自然现象的原理是非常像的,所以理解了这种自然现象,就对于理解Dijkstra算法有非常大的帮助。
Dijkstra执行过程
假设现在有如下的有向图
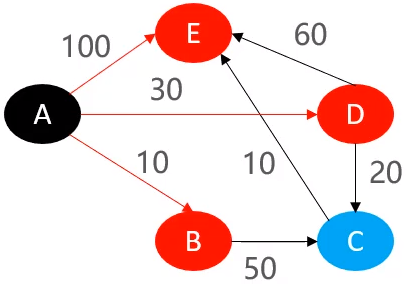
现在同样是计算A到其他顶点之间的最短路径,模拟刚刚的自然现象的话,就相当于现在要将石头A拽起来,其他小石头现在还在桌面,现在要计算A到其他顶点之间的最短路径,A就是最先被拉起来的小石头。然后上图中有不同的颜色,其中黑色表示最短路径的源头,红色表示与刚刚被拉起来的顶点直接相连的顶点,蓝色表示不是与刚刚被拉起来的顶点直接相连的顶点。
由于现在A已经离开桌面了,所以下一个即将被拽起来的石头,一定是B,D,E中的其中一个石头,因为B,D,E是与A直接相连的,C不能再A离开以后的下一个离开桌面,因为B还没有离开桌面。并且与A直接相连的三个顶点,其中权值最小的顶点将会成为下一个离开桌面的石头,被A拽起来。
所以现在由于A已经被拽起来,离开了桌面,下一个即将被拽起来的石头,一定是B,D,E中的其中一个石头。所以B,D,E是有机会成为下一个离开桌面的石头。那么在A离开桌面以后,就更新一下A到B,D,E之间的距离,用来表示A到其他顶点之间的最短路径,更新的表格结果如下
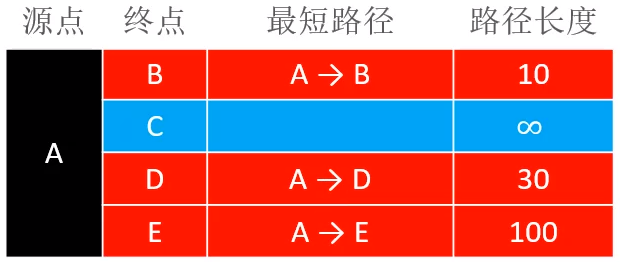
通过顶点A的outEdges,目前能直接得到的A→B,A→D,A→E的权值,就如上表所示、由于现在C并没有与A直接相连,所以A并不知道C的存在,因此A→C的权值,目前就用∞来进行表示。
通过这个表,就可以确定,下一步哪个石头即将离开桌面,所以根据上面的数据,离A最近的石头B将成为下一个离开桌面的石头,离开后的结果如下
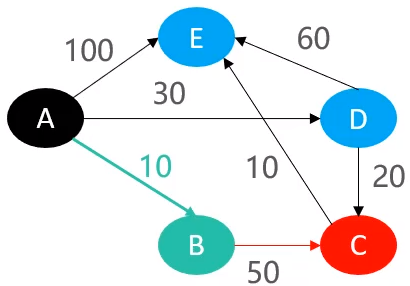
由于B已经离开桌面,也就意味着,A到B之间的最短路径已经确定。并且由于B已经离开桌面,所以与B直接相连的C也成为了下一个可能即将离开桌面的石头,那么就可以认为C目前最有可能被B拽起来,所以认为A到C之间的最短路径可能是A→B→C的路径,所以更新表格,得到的数据如下
- 绿色:表示已经离开桌面,并且是确定的最短路径,后面不用再考虑这条路径
- 红色:表示更新了的最短路径信息
- 蓝色:表示本次更新没有修改
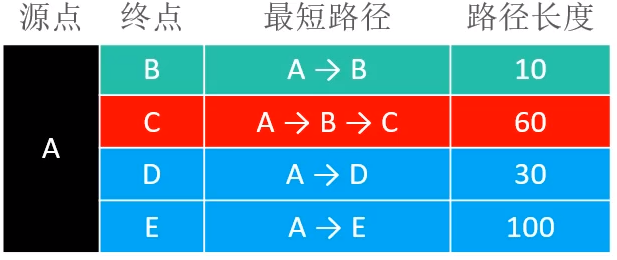
通过这个表格,你可能会想,为什么不通过A→D→C这条路径来将C拽起来呢?很简单,因为现在D还没有离开桌面,所以D目前就没有能力将C从桌面拽起来,只有B才有可能。最终在下一个离开桌面的石头中,可能是A拽来的E或者D,也可能是B拽起来的C,至于到底哪个石头将会被拽起来,则取决于他们与A之间的路径。
从上表中可以很明显的看出,没有离开桌面的C,D,E中,离A最近的是D,所以下一个即将被拽起来的是D,所以D离开桌面以后的结果如下
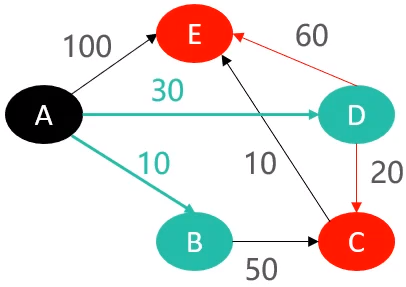
由于现在D已经离开桌面了,并且发现D与E,C之间同样连接着一根线,也就意味着,石头E和石头C有新的选择。
为什么呢?就拿E来说,在D没有被拽起来离开桌面之前,E只可能被A拽起来离开桌面,而现在D被拽起来了以后,E就可能既被A拽起来离开桌面,也可能被D拽起来离开桌面,至于最终被谁拽起来,则取决于A→E之间的权重与A→D→E之间的权重谁更小。
根据上面的解释,也就意味着E和C均多了一种被D拽起来离开桌面的可能。所以当D被拽起来离开桌面以后,就更新A到C,A到E之间的路径长度,所以更新后的表格如下

接下来,哪个石头将被拽起来,同样是依据表格中还没有被拽起来石头中个,哪个石头到原点A之间的距离最小,最小的就将被拽起来。很明显,下一个将被拉起来的石头是C,拽起来以后的结果如下
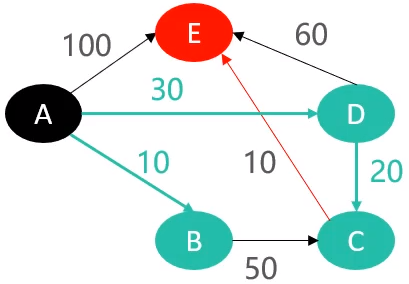
到现在,A,B,C,D都被拽起来了,而且请注意,一旦C被拽起来,也就意味着E又多了一种新的选择。因为在C被拽起来之前,认为E可能是通过A→D→E这条路径,将E拽起来的。但是现在C也被拽起来了,所以E有可能通过A→D→C→E这条路径被拽起来。所以就比较这两条路径,哪条路径的路径长度更短,最终比较发现是通过A→D→C→E这条路径是更短的,所以更新表格中的路径长度
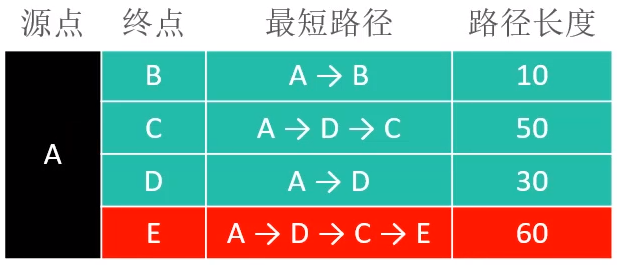
由于到现在,没有被拽起来的石头只有E,所以下一个被拽起来的石头就是E,并且通过A→D→C→E这条路径被转起来的。
最终,下图中绿色的线,就是最终被绷直的线
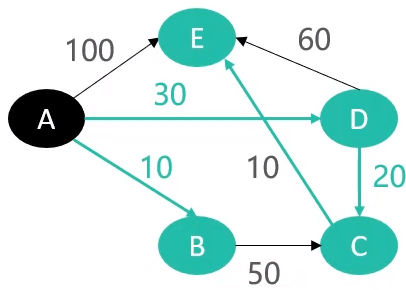
最短路径对应的表格如下
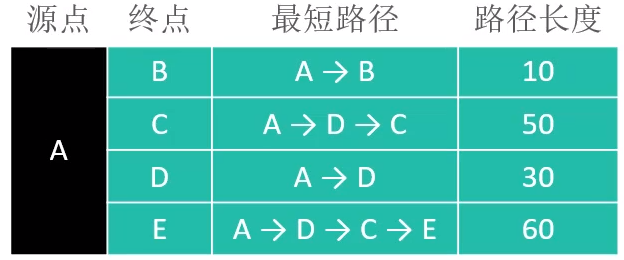
以上的这个过程,就是通过Dijkstra算法计算最短路径的流程。
松弛操作(Relaxation)
松弛操作:表示更新两个顶点之间最短路径
例如前面D被拉起来以后,C和E都多了一种被拉起来的选择,就是E可能被A拉起来,也可能被D拉起来;C可能被D拉起来,也可能被B拉起来。具体在D被来起来以后,C和E将被哪个石头拉起来,就需要更新C到A之间的路径,更新E到A之间的路径。这种更新两个顶点之间的路径的操作,就叫做松弛操作。也就是说,确定A到D的最短路径以后,对DC,DE边进行松弛操作,更新了A到C,A到E的最短路径。
在这里的松弛操作,一般指的是,更新源点到另一个点之间的最短路径。
所以前面的过程,通过松弛操作来进行阐述的话,就是
- 一旦有石头被拽起来,就需要对该石头的outEdges进行松弛操作,计算出outEdges这些顶点被拽起来的最短路径。
- 所以当A被拽起来以后,就需要对AB,AD,AE这些边进行松弛操作,更新这些边到原点之间的最短路径
- 找出路径长度最短的点,通过上面的表格可以知道,当前路径最短的是A→B这条路径,所以B被拽起来
- B一旦被拽起来,也就意味着A到B之间的最短路径确定了,然后对B的outEdges进行松弛操作,由于目前B的outEdges只有一条表BC,所以现在对BC边进行松弛操作
- 基础超出路径长度最小的顶点,所以这一次,D被拽了起来
- D被拽起来了以后,又会对D的outEdges进行一次松弛操作,所以会对DE,DC这两条边进行松弛操作
- 就依照这种流程,一直重复,直到确定所有顶点的最短路径,算法就结束了。
Dijkstra实现
结合前面的分析,最终要实现的是计算出某个顶点到其他顶点的最短路径。
其中要计算出最短路径,则有以下几个关键步骤:
- 每当有一个顶点被拽起来以后,就会从对路径发生变化的顶点进行松弛操作,在不断松弛的过程中,会更新该顶点到其他顶点之间的最短路径长度
- 选择一个路径长度最短的顶点,作为下一个即将离开桌面的顶点
- 重复以上两个步骤
所以结合这个思路,可以得到计算最短路径的大概框架
public Map<V, E> shortestPath(V begin) {
Vertex beginVertex = vertices.get(begin);
if (beginVertex == null) return null;
Map<V, E> selectedPaths = new HashMap<>();
Map<Vertex<V,E>, E> paths = new HashMap<>();
while (!paths.isEmpty()) {
Map.Entry<Vertex<V,E>,E> minEntry = getShortestPath(paths);
//minEntry离开桌面
Vertex<V,E> minVertex = minEntry.getKey();
selectedPaths.put(minVertex.value,minEntry.getValue());
paths.remove(minVertex);
//对minVertex的outEdges进行松弛操作
for (Edge<V,E> edge : minVertex.outEdges) {
relax();
}
}
return selectedPaths;
}
/*
* 从paths中选出一个最短的路径出来
* */
private Map.Entry<Vertex<V,E>,E> getShortestPath(Map<Vertex<V,E>, E> paths) {
return null;
}
/*
* 进行松弛操作
* */
private void relax() {
}
其中selectedPaths这个Map用来保存已经计算出最短路径的顶点,paths这个Map用来保存下一个即将离开桌面的顶点。当paths中的所有顶点都计算出最短路径以后,说明整个最短路径就计算完毕了。
结合上面的框架,与前面的分析思路,最终得到的基础版本实现如下
public Map<V, E> shortestPath(V begin) {
Vertex<V,E> beginVertex = vertices.get(begin);
if (beginVertex == null) return null;
Map<V, E> selectedPaths = new HashMap<>();
Map<Vertex<V,E>, E> paths = new HashMap<>();
//初始化paths
for (Edge<V,E> edge: beginVertex.outEdges) {
paths.put(edge.to,edge.weight);
}
while (!paths.isEmpty()) {
Map.Entry<Vertex<V,E>,E> minEntry = getShortestPath(paths);
//minEntry离开桌面
Vertex<V,E> minVertex = minEntry.getKey();
selectedPaths.put(minVertex.value,minEntry.getValue());
paths.remove(minVertex);
//对minVertex的outEdges进行松弛操作
for (Edge<V,E> edge : minVertex.outEdges) {
//如果edge.to已经离开桌面,就没必要进行松弛操作
if (selectedPaths.containsKey(edge.to.value)) continue;;
//relax();
//新的可选的最短路径:beginVertex到edge.from的最短路径 + edge.weight
//minEntry.getValue() + edge.weight;
E newWeight = weightManager.add(minEntry.getValue(),edge.weight);
//以前的最短路径:beginVertex到edge.to的最短路径
E oldWeight = paths.get(edge.to);
//比较两个路径长度
if (oldWeight == null || weightManager.compare(newWeight,oldWeight) < 0) {
//如果新的路径长度比旧的路径更短,或者原来没有旧的路径长度,就更新路径长度
paths.put(edge.to,newWeight);
}
}
}
//如果是无向图,前面会将起点也添加进去,所以最后将起点删除掉
selectedPaths.remove(begin);
return selectedPaths;
}
/*
* 从paths中选出一个最短的路径出来
* */
private Map.Entry<Vertex<V,E>,E> getShortestPath(Map<Vertex<V,E>, E> paths) {
Iterator<Map.Entry<Vertex<V,E>,E>> it = paths.entrySet().iterator();
Map.Entry<Vertex<V,E>,E> minEntry = it.next();
while (it.hasNext()) {
Map.Entry<Vertex<V,E>,E> entry = it.next();
if (weightManager.compare(entry.getValue(),minEntry.getValue()) < 0) {
minEntry = entry;
}
}
return minEntry;
}
所以上面的代码,就是完完全全按照前面的分析,结合将小石头从桌子上提起来这种生活现象,对Dijkstra这种单源最短路径算法进行实现。所以可以发现整体的思路还是挺简单的,而且代码也不复杂。
但是目前上面这种算法,返回的内容是终点与原点之间,对应的路径长度。并没有包含是通过哪些顶点计算出来的最短路径。所以有时候可能希望返回的数据里面,包含了从原点到达终点时,经过了哪些顶点。所以需要将上面的算法进行改进
Dijkstra改进
为了达到前面想要实现的功能,所以需要对返回的数据进行修改。在返回的Map中,将经过的最短路径也保存到Map中,这样返回的结果就跟全面了。
首先要改进的地方是对接口进行修改。在前面的Map中,每一个键值对中,key(顶点)对应的value是权值,所以现在要将顶点对应的信息修改为边的信息+ 权值,这样就能拿到最终计算出最短路径时,经过的路径信息。
最终经过改进后的算法如下:
public Map<V, PathInfo<V, E>> shortestPath(V begin) {
Vertex<V,E> beginVertex = vertices.get(begin);
if (beginVertex == null) return null;
Map<V, PathInfo<V, E>> selectedPaths = new HashMap<>();
Map<Vertex<V,E>, PathInfo<V, E>> paths = new HashMap<>();
//初始化paths
for (Edge<V,E> edge: beginVertex.outEdges) {
PathInfo<V,E> path = new PathInfo<V,E>();
path.setWeight(edge.weight);
path.edgeInfos.add(edge.info());
paths.put(edge.to,path);
}
while (!paths.isEmpty()) {
Map.Entry<Vertex<V,E>, PathInfo<V,E>> minEntry = getShortestPath(paths);
//minEntry离开桌面
Vertex<V,E> minVertex = minEntry.getKey();
selectedPaths.put(minVertex.value,minEntry.getValue());
paths.remove(minVertex);
//对minVertex的outEdges进行松弛操作
for (Edge<V,E> edge : minVertex.outEdges) {
//如果edge.to已经离开桌面,就没必要进行松弛操作
if (selectedPaths.containsKey(edge.to.value)) continue;;
//relax();
//新的可选的最短路径:beginVertex到edge.from的最短路径 + edge.weight
//minEntry.getValue() + edge.weight;
E newWeight = weightManager.add(minEntry.getValue().weight,edge.weight);
//以前的最短路径:beginVertex到edge.to的最短路径
PathInfo<V,E> oldPath = paths.get(edge.to);
//比较两个路径长度
if (oldPath == null || weightManager.compare(newWeight,oldPath.weight) < 0) {
//如果新的路径长度比旧的路径更短,或者原来没有旧的路径长度,就更新路径长度
PathInfo<V,E> path = new PathInfo<>();
path.weight = newWeight;
path.edgeInfos.addAll(minEntry.getValue().edgeInfos);
path.edgeInfos.add(edge.info());
paths.put(edge.to,path);
}
}
}
//如果是无向图,前面会将起点也添加进去,所以最后将起点删除掉
selectedPaths.remove(begin);
return selectedPaths;
}
/*
* 从paths中选出一个最短的路径出来
* */
private Map.Entry<Vertex<V,E>, PathInfo<V,E>> getShortestPath(Map<Vertex<V,E>, PathInfo<V,E>> paths) {
Iterator<Map.Entry<Vertex<V,E>, PathInfo<V,E>>> it = paths.entrySet().iterator();
Map.Entry<Vertex<V,E>, PathInfo<V,E>> minEntry = it.next();
while (it.hasNext()) {
Map.Entry<Vertex<V,E>, PathInfo<V,E>> entry = it.next();
if (weightManager.compare(entry.getValue().weight,minEntry.getValue().weight) < 0) {
minEntry = entry;
}
}
return minEntry;
}
然后将以上代码进行优化后,结果如下
public Map<V, PathInfo<V, E>> shortestPath(V begin) {
Vertex<V,E> beginVertex = vertices.get(begin);
if (beginVertex == null) return null;
Map<V, PathInfo<V, E>> selectedPaths = new HashMap<>();
Map<Vertex<V,E>, PathInfo<V, E>> paths = new HashMap<>();
//初始化paths
for (Edge<V,E> edge: beginVertex.outEdges) {
PathInfo<V,E> path = new PathInfo<V,E>();
path.setWeight(edge.weight);
path.edgeInfos.add(edge.info());
paths.put(edge.to,path);
}
while (!paths.isEmpty()) {
Map.Entry<Vertex<V,E>, PathInfo<V,E>> minEntry = getShortestPath(paths);
//minEntry离开桌面
Vertex<V,E> minVertex = minEntry.getKey();
PathInfo<V,E> minPath = minEntry.getValue();
selectedPaths.put(minVertex.value,minPath);
paths.remove(minVertex);
//对minVertex的outEdges进行松弛操作
for (Edge<V,E> edge : minVertex.outEdges) {
//如果edge.to已经离开桌面,就没必要进行松弛操作
if (selectedPaths.containsKey(edge.to.value)) continue;;
relax(edge,paths,minPath);
}
}
//如果是无向图,前面会将起点也添加进去,所以最后将起点删除掉
selectedPaths.remove(begin);
return selectedPaths;
}
/*
* 从paths中选出一个最短的路径出来
* */
private Map.Entry<Vertex<V,E>, PathInfo<V,E>> getShortestPath(Map<Vertex<V,E>, PathInfo<V,E>> paths) {
Iterator<Map.Entry<Vertex<V,E>, PathInfo<V,E>>> it = paths.entrySet().iterator();
Map.Entry<Vertex<V,E>, PathInfo<V,E>> minEntry = it.next();
while (it.hasNext()) {
Map.Entry<Vertex<V,E>, PathInfo<V,E>> entry = it.next();
if (weightManager.compare(entry.getValue().weight,minEntry.getValue().weight) < 0) {
minEntry = entry;
}
}
return minEntry;
}
private void relax(Edge<V,E> edge, Map<Vertex<V,E> ,PathInfo<V,E>> paths, PathInfo<V,E> fromPath) {
//新的可选的最短路径:beginVertex到edge.from的最短路径 + edge.weight
//minEntry.getValue() + edge.weight;
E newWeight = weightManager.add(fromPath.weight,edge.weight);
//以前的最短路径:beginVertex到edge.to的最短路径
PathInfo<V,E> oldPath = paths.get(edge.to);
//如果新的路径大于等于原来路径,就不用做任何操作
if (oldPath != null && weightManager.compare(newWeight,oldPath.weight) >= 0) return;
if (oldPath == null) {
oldPath = new PathInfo<>();
paths.put(edge.to,oldPath);
}else {
oldPath.edgeInfos.clear();
}
oldPath.weight = newWeight;
oldPath.edgeInfos.addAll(fromPath.edgeInfos);
oldPath.edgeInfos.add(edge.info());
paths.put(edge.to,oldPath);
}
到这里,就将Dijkstra计算原点到其他点的最短路径计算出来了。不过这种算法并不是最优的算法,因为在从paths中选出一个最短的路径出来时,使用的是便于理解的遍历比较来实现的,这种算法,效率比较低,在前面有介绍过使用堆这种数据结构来获取最值,效率非常高。所以如果要优化的话, 可以考虑在从paths中选出一个最短的路径出来时,使用最小堆这种数据结构来实现。
完!