线性代数精华1——从行列式开始

本文始发于个人公众号：TechFlow

线性代数是机器学习领域当中非常重要的基础知识，但是很遗憾的是，在真正入门之前很少有人能认识到它的重要性，将它学习扎实，在入门之后，再认识到想要补课也不容易。我自己也是一样，大学期间只是浅尝辄止，这门课考试成绩还可以，但是过后记住的内容不多。导致后来在看很多论文以及资料的时候，很吃力，很多公式很难看懂，即使看懂了也很容易忘记。

线性代数的内容不少，许多非常精深，这里我们只提炼最关键的知识点。没学过的同学可以很容易get到精髓，学过的同学也可以当做复习。

行列式定义

维基百科中的定义是，行列式是一个函数，将一个n * n的矩阵映射到一个标量。这个标量表示经过这个矩阵所代表的的线性变幻之后，矩阵的“体积”在空间当中发生的变化。

也就是说，行列式的输入是一个n * n的方阵，输出是一个具体的数。我们把行列式用det来表示，假设A是某一个n * n的矩阵，那么det(A)即表示该矩阵的行列式。

行列式计算

二阶行列式

令

A=\left|
\begin{matrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{matrix}
\right|

那么 $det(A)= a_{11} * a_{22} - a{12} * a_{21}$ ，即为对角线乘积的差。

三阶行列式

再来看三阶的情况：

令

B=\left|
\begin{matrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{matrix}
\right|

那么 $det(B) = a_{11} * a_{22} * a_{33} + a_{12} * a_{23} * a_{31} + a_{13} * a_{21} * a_{32} - a_{11} * a_{23} * a_{32} - a_{12} * a_{21} * a_{33} - a_{13} * a_{22} * a_{31}$

光看公式非常复杂，如果我们把所有正项的乘积用红线相连，把负项的成绩用蓝线相连，那么我们可以得到下面这张图。

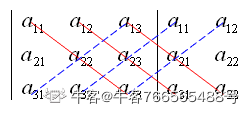
其实本质上来说，还是对角线的乘积差，即所有正向（从左上往右下）对角线的乘积和减去反向（从右上往左下）对角线的乘积和。

我们列出了二项以及三项行列式的式子，自然而然，我们下面就要写出n项行列式的计算方法。但在此之前，我们先要引入另外一个相关的概念——逆序数。

逆序数

逆序数本身主要就是应用在行列式的计算当中，不过除此之外在面试题当中经常出现，许多面试题会让求职者写出或口述逆序数的计算算法。关于这点，会在之后的算法专栏当中单独讲解。

假设我们有一个数组A，它当中有n个各不相同的元素。在理想情况下，A当中的元素应该都是有序的。比如说都是从小到大排列，但理想情况很少发生。大多数情况下，数组当中的元素都是无序的。

假如我们想要知道，数组当前的排序距离理想情况的升序究竟有多大的差距。很正常地可以想到，我们可以遍历这个数组当中所有 $A_i$ 和 $A_j$ 的组合，看看究竟有多少数的次序有误。在这个序列所有两两元素的组合当中，有误的次序的组合总数就叫做逆序数。

光看概念有些拗口，但是直接看代码的话其实非常简单：

reverse = 0
for i in range(n):
  for j in range(i):
    if A[i] < A[j]:
      reverse += 1

也就是说我们对于数组当中的每一个元素，都计算出了排在它前面并且比它大的元素个数。考虑一般情况，假设A数组的排列为 $p_1, p_2, p_3,...,p_n$ ，对于每一个 $p_i$ 我们都求出它前面比较大的元素个数，定义为 $t_i$ ，那么全体的逆序数之和：

n阶行列式

我们再回到n阶行列式来，理解了逆序数的概念之后，我们就很方便地可以写出n阶行列式的公式了。

首先，先定义出矩阵D，是一个n阶的方阵：

D=\left|
\begin{matrix}
a_{11} & a_{12} & ... & a_{1n} \\
a_{21} & a_{22} & ... & a_{2n} \\
\vdots & \vdots & & \vdots \\
a_{n_1} & a_{n_2} & ... & a_{nn}
\end{matrix}
\right|

假设自然数 $1, 2, 3...n$ 的一个排列为 $p_1, p_2, p_3,...,p_n$ ，这个排列的逆序数为t。那么我们可以写出D的行列式：

det(D) = \sum(-1)^t a_{1_{p1}}a_{2_{p2}}...a_{n_{pn}}

由于长度为n的序列的全排列一共有 $n!$ 种，所以n阶方阵的行列式一共含有 $n!$ 项。

除此之外，行列式还有另外一种计算方法。

在n阶行列式当中，把 $(i,j)$ 元素所在的行和列的所有元素全部去除之后，剩下的新的n-1阶的行列式称为 $(i, j)$ 元的代数余子式，记为 $M_{ij}$

列入4阶行列式：

D=\left|
\begin{matrix}
a_{11} & a_{12} & a_{13} & a_{14} \\
a_{21} & a_{22} & a_{23} & a_{24} \\
a_{31} & a_{32} & a_{33} & a_{34} \\
a_{41} & a_{42} & a_{43} & a_{44}
\end{matrix}
\right|

其中 $(2, 2)$ 元的代数余子式为：

M_{22}=\left|
\begin{matrix}
a_{11} & a_{13} & a_{14} \\
a_{31} & a_{33} & a_{34} \\
a_{41} & a_{42} & a_{44}
\end{matrix}
\right|

代数余子式可以用来表示行列式：

$A$ 矩阵的行列式可以写成： $\sum_{i=1}^na_{1i}M_{1i}$

证明也很简单，其实这只不过是行列式表达式的一个变形。我们用三阶行列式举例：

$|A| = a_{11}(a_{22}a_{33} - a_{23}a_{32}) + a_{12}(a_{23}a_{31}-a_{21}a_{33}) + a_{13}(a_{21}a_{32}-a_{22}a_{31})$

我们把这些值用代数余子式表示出来：

\left|
\begin{matrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{matrix}
\right|=\left|
\begin{matrix}
a_{11} & & \\
& a_{22} & a_{23}\\
& a_{32} & a_{33}
\end{matrix}
\right|+\left|
\begin{matrix}
& a_{12} & \\
a_{21} & & a_{23}\\
a_{31} & & a_{33}
\end{matrix}
\right|+\left|
\begin{matrix}
& & a_{13}\\
a_{21} & a_{22} & \\
a_{31} & a_{32} &
\end{matrix}
\right|

化简一下，显然就是上面公式的结果。

克拉默法则

行列式的定义和计算都不太直观，那么这么一个相对比较复杂的概念究竟有什么作用呢？

除了用在机器学习的模型当中之外，另一个非常经典的用途就是判断线性方程组是否有解。

对于一个含有n个未知数的n个线性方程组

\begin{cases}
a_{11}x_1 + a_{12}x_2 + ... + a_{1n}x_n = b_1 \\
a_{21}x_1 + a_{22}x_2 + ... + a_{2n}x_n = b_2 \\
......\\
a_{n1}x_1 + a_{n2}x_2 + ... + a_{nn}x_n = b_n
\end{cases}

它的解可以用n阶行列式表示。

如果这个n阶的行列式不等于0，即：

det(D)=\left|
\begin{matrix}
a_{11} & ... & a_{1n} \\
\vdots & & \vdots \\
a_{n1} & ... & a_{nn}
\end{matrix}
\right|\neq 0

那么这个n阶方程组有唯一解，并且它的解为：

$x_1=\frac{D1}{D} x_2=\frac{D2}{D} ... x_n=\frac{D_n}{D}$

其中 $D_j(j=1,2,...n)$ 是把D中第j列替换成方程常数项得到的新的行列式：

D_j=\left|
\begin{matrix}
a_{11} & ... & a_{1,j-1} & b_1 & a_{1, j+1} & ... & a_{1n} \\
\vdots & & \vdots & \vdots & \vdots & & \vdots \\
a_{n1} & ... & a_{n,j-1} & b_n & a_{n, j+1} & ... & a_{nn}
\end{matrix}
\right|

行列式除了上面提到的内容之外，还有很多很好用的性质以及一些变种的计算方法。不过，对于算法领域的帮助不多，所以这里不多枚举，感兴趣的同学可以自己查阅相关资料。

行列式的几何意义

行列式除了代数上的作用之外，也是有它的几何意义的。

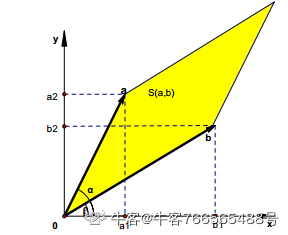
以二阶行列式举例，假设我们有A，B两个向量，其中A向量写作 $(a_1, b_1)$ ，B向量写作 $(b_1, b_2)$ ，AB两个向量组合成的矩阵写作：

Mat(A, B) = \left|
\begin{matrix}
a_1 & a_2 \\
b_1 & b_2
\end{matrix}
\right|

如果我们将它画出来，它其实表示这两个向量的平行四边形面积

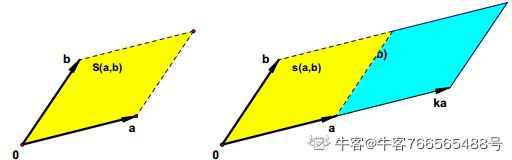
所以，当我们把行列式当中的某一行或者是某一列同时乘上一个系数k之后，它的行列式增大了k倍。

代码计算

从上文行列式的定义很容易得出结论，行列式的计算比较复杂，如果我们自己实现，需要的代码至少在100行以上。不过好在Python的Numpy库当中为我们提供了非常丰富的矩阵相关操作，包括行列式的计算在内，因此，我们可以非常简单的实现行列式的计算。

如果没有装过Numpy的，可以通过pip很方便地安装：

pip install numpy

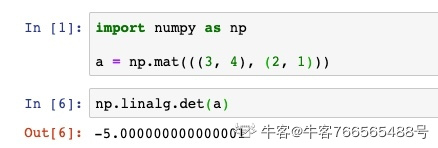
通过调用numpy.linalg中的det函数，我们可以直接求出矩阵行列式的值。

参考资料

维基百科

线性代数第五版（上海交大出版社）

www.cnblogs.com/andyjee/p/3…