散列表与散列算法
散列表的英文叫“Hash Table”,我们平时也叫它“哈希表”或者“Hash 表”,散列表用的是数组支持按照下标随机访问数据的特性,所以散列表其实就是数组的一种扩展,由数组演化而来。可以说,如果没有数组,就没有散列表。
散列思想
通过一个例子学习散列的思想。
假如我们有 89 名选手参加学校运动会。为了方便记录成绩,每个选手胸前都会贴上自己的参赛号码。这 89 名选手的编号依次是 1 到 89。现在我们希望编程实现这样一个功能,通过编号快速找到对应的选手信息。你会怎么做呢?我们可以把这 89 名选手的信息放在数组里。编号为 1 的选手,我们放到数组中下标为 1 的位置;编号为 2 的选手,我们放到数组中下标为 2 的位置。以此类推,编号为 k 的选手放到数组中下标为 k 的位置。因为参赛编号跟数组下标一一对应,当我们需要查询参赛编号为 x 的选手的时候,我们只需要将下标为 x 的数组元素取出来就可以了,时间复杂度就是 O(1)。这样按照编号查找选手信息,效率是不是很高?
实际上,这个例子已经用到了散列的思想。在这个例子里,参赛编号是自然数,并且与数组的下标形成一一映射,所以利用数组支持根据下标随机访问的时候,时间复杂度是 O(1) 这一特性,就可以实现快速查找编号对应的选手信息。但是这个例子散列思想还不够明显,那我来改造一下这个例子。
假设校长说,参赛编号不能设置得这么简单,要加上年级、班级这些更详细的信息,所以我们把编号的规则稍微修改了一下,用 6 位数字来表示。比如 051167,其中,前两位 05 表示年级,中间两位 11 表示班级,最后两位还是原来的编号 1 到 89。这个时候我们该如何存储选手信息,才能够支持通过编号来快速查找选手信息呢?思路还是跟前面类似。尽管我们不能直接把编号作为数组下标,但我们可以截取参赛编号的后两位作为数组下标,来存取选手信息数据。当通过参赛编号查询选手信息的时候,我们用同样的方法,取参赛编号的后两位,作为数组下标,来读取数组中的数据。
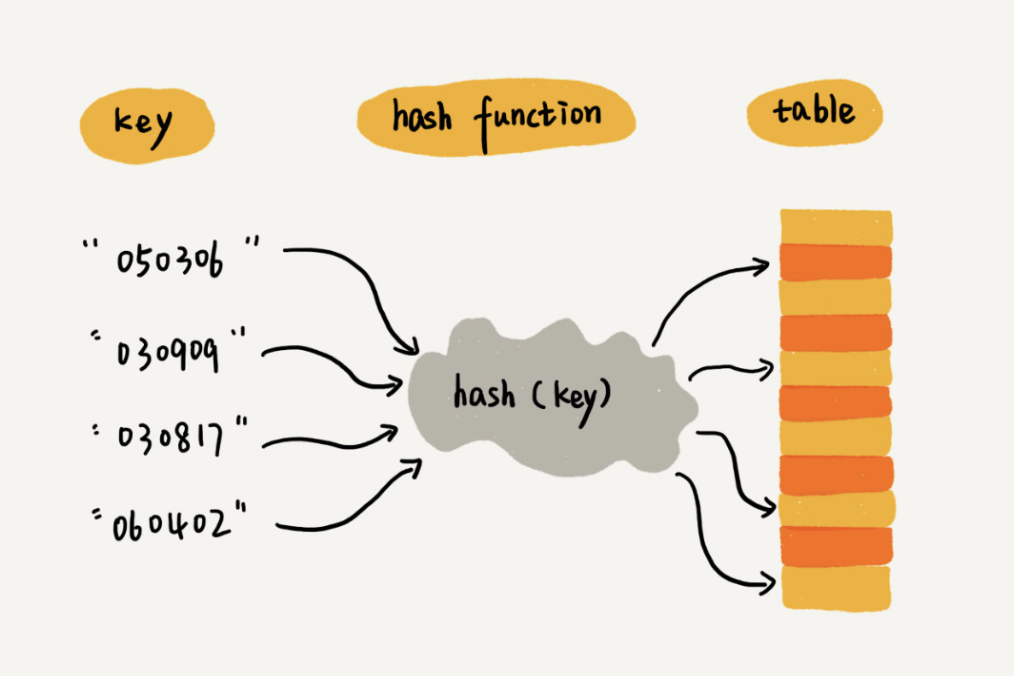
这就是典型的散列思想。其中,参赛选手的编号我们叫作键(key)或者关键字。我们用它来标识一个选手。我们把参赛编号转化为数组下标的映射方法就叫作散列函数(或“Hash 函数”“哈希函数”),而散列函数计算得到的值就叫作散列值(或“Hash 值”“哈希值”)。
总结规律
散列表用的就是数组支持按照下标随机访问的时候,时间复杂度是 O(1) 的特性。我们通过散列函数把元素的键值映射为下标,然后将数据存储在数组中对应下标的位置。当我们按照键值查询元素时,我们用同样的散列函数,将键值转化数组下标,从对应的数组下标的位置取数据。
代码实例




/**
* @description 在字典中我们是用键值对来存储数据
*/
const assert = require("assert");
// 散列函数
const loseloseHashCode = (key = '') => {
let hashCode = 0
for(let i = 0; i < key.length; i++) {
hashCode += key.charCodeAt(i)
}
return hashCode % 37
}
class HashTable {
constructor() {
this.table = []
}
put(key, value) {
this.table[loseloseHashCode(key)] = value
}
remove(key) {
const position = loseloseHashCode(key)
if (this.table[position]) {
// 不能删除该行,因为会影响其他数组的位置
this.table[position] = undefined
return true
}
return false
}
get(key) {
return this.table[loseloseHashCode(key)]
}
getItems() {
return this.table
}
}
// test case
const hashTable = new HashTable()
hashTable.put("Jobs", "Jobs@qq.com");
hashTable.put("Bob", "Bob@qq.com");
console.log(hashTable.getItems());
assert.strictEqual(hashTable.remove('Bob'), true);
console.log(hashTable.getItems());
assert.strictEqual(hashTable.get('Jobs'), 'Jobs@qq.com');
散列表冲突问题
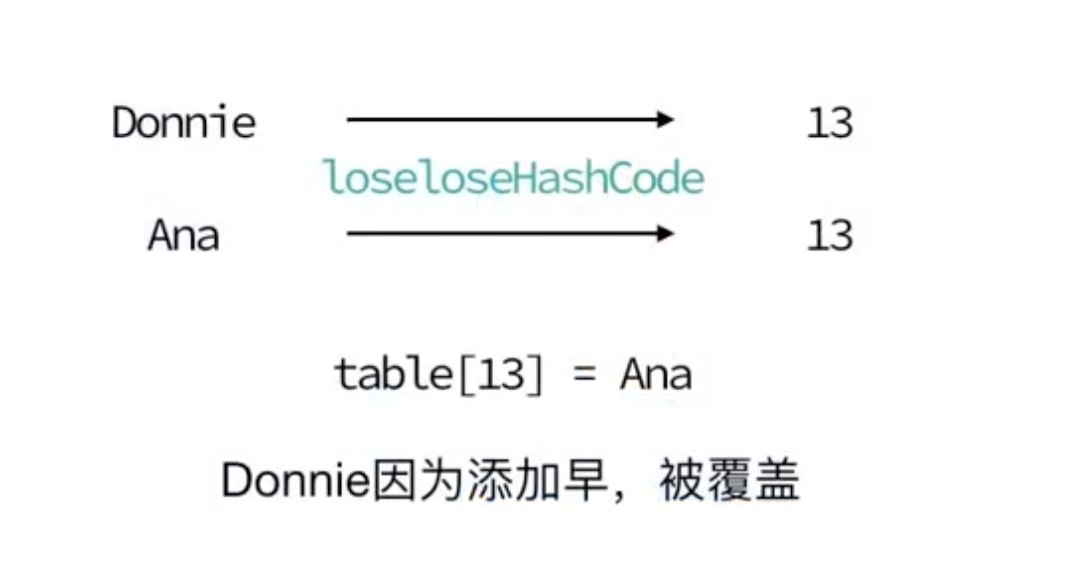
在真实的情况下,要想找到一个不同的 key 对应的散列值都不一样的散列函数,几乎是不可能的。即便像业界著名的MD5、SHA、CRC等哈希算法,也无法完全避免这种散列冲突。而且,因为数组的存储空间有限,也会加大散列冲突的概率。所以我们几乎无法找到一个完美的无冲突的散列函数,即便能找到,付出的时间成本、计算成本也是很大的,所以针对散列冲突问题,我们需要通过其他途径来解决。
分离链接法
在散列表中,每个“桶(bucket)”或者“槽(slot)”会对应一条链表,所有散列值相同的元素我们都放到相同槽位对应的链表中。
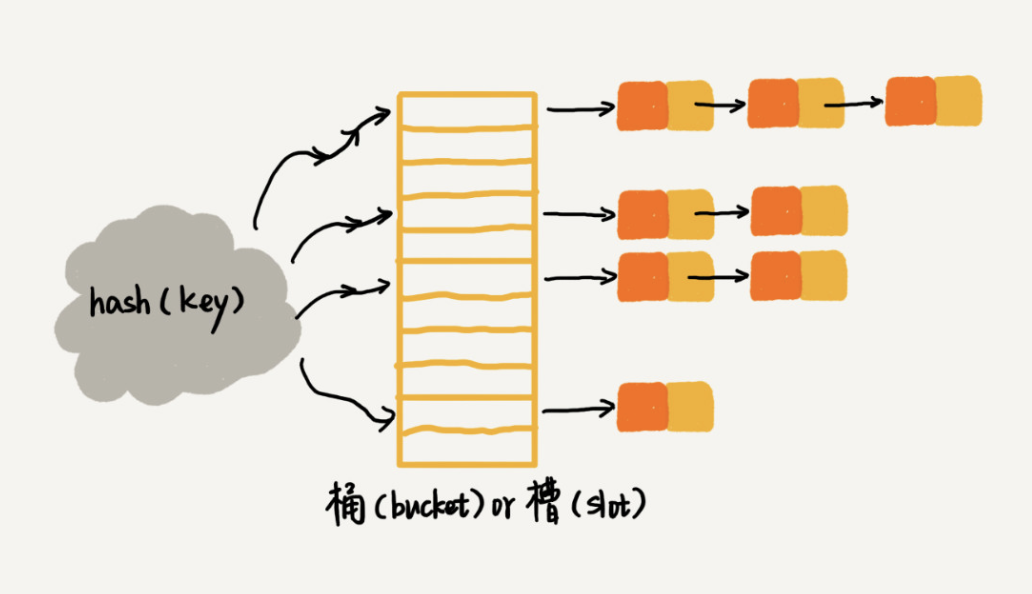
当插入的时候,我们只需要通过散列函数计算出对应的散列槽位,将其插入到对应链表中即可,所以插入的时间复杂度是 O(1)。当查找、删除一个元素时,我们同样通过散列函数计算出对应的槽,然后遍历链表查找或者删除。那查找或删除操作的时间复杂度是多少呢?实际上,这两个操作的时间复杂度跟链表的长度 k 成正比,也就是 O(k)。对于散列比较均匀的散列函数来说,理论上讲,k=n/m,其中 n 表示散列中数据的个数,m 表示散列表中“槽”的个数。
/**
* @description 在字典中我们是用键值对来存储数据
*/
const assert = require("assert");
class Node {
constructor(element) {
this.element = element;
this.next = null;
}
}
class LinkedList {
constructor() {
this.head = null;
this.length = 0;
}
// 在链表尾部追加结点
append(element) {
const addNode = new Node(element);
// 空链表
if (this.isEmpty()) {
this.head = addNode;
} else {
// 非空链表,先找到链表尾部
let cur = this.head;
while (cur.next) {
cur = cur.next;
}
cur.next = addNode;
}
this.length += 1;
}
insert(position, element) {
// 边界情况处理
if (
(Number.isInteger(position) && position > -1) ||
position < this.size()
) {
const addNode = new Node(element);
let cur = this.head;
let prev = null;
// 在链表头位置插入
if (position === 0) {
this.head = addNode;
addNode.next = cur;
} else {
// 在其他位置插入
let index = 0;
while (index < position) {
prev = cur;
cur = cur.next;
index++;
}
prev.next = addNode;
addNode.next = cur;
}
this.length++;
}
}
removeAt(position) {
if (
(Number.isInteger(position) && position > -1) ||
position < this.size()
) {
let cur = this.head;
// 移除链表头
if (position === 0) {
this.head = cur.next;
} else {
// 移除其他元素
let index = 0;
let prev = null;
while (index < position) {
prev = cur;
cur = cur.next;
index++;
}
prev.next = cur.next;
}
this.length--;
return cur;
}
return null;
}
indexOf(element) {
let index = 0;
let cur = this.head;
while (cur) {
if (cur.element === element) {
return index;
}
cur = cur.next;
index++;
}
return -1;
}
remove(element) {
return this.removeAt(this.indexOf(element));
}
isEmpty() {
return this.length === 0;
}
size() {
return this.length;
}
}
// 散列函数
const loseloseHashCode = (key = "") => {
let hashCode = 0;
for (let i = 0; i < key.length; i++) {
hashCode += key.charCodeAt(i);
}
return hashCode % 37;
};
class patchValue {
constructor(key, value) {
this.key = key;
this.value = value;
}
}
class HashTableLinked {
constructor() {
this.table = [];
}
put(key, value) {
const position = loseloseHashCode(key);
if (!this.table[position]) {
// 第一次初始化链表
this.table[position] = new LinkedList()
}
this.table[position].append(new patchValue(key, value));
}
remove(key) {
const position = loseloseHashCode(key);
if (this.table[position]) {
let cur = this.table[position].head;
while (cur) {
if (cur.element.key === key) {
// 找到Node结点
this.table[position].remove(cur.element)
// 空链表需要重新初始化
if (this.table[position].isEmpty()) {
this.table[position] = undefined;
}
return true;
}
cur = cur.next;
}
return false;
}
return false;
}
get(key) {
const position = loseloseHashCode(key);
if (this.table[position]) {
let cur = this.table[position].head;
while (cur) {
if (cur.element.key === key) {
return cur.element.value;
}
cur = cur.next;
}
return undefined;
} else {
return undefined;
}
}
getItems() {
return this.table;
}
}
// test case
const hashTable = new HashTableLinked();
hashTable.put("Donnie", "Donnie@qq.com");
hashTable.put("Ana", "Ana@qq.com");
console.log(hashTable.getItems()[13]);
hashTable.remove("Donnie");
hashTable.remove("Ana");
console.log(hashTable.getItems()[13]);
参考资料
PS: 有兴趣的关注我的公众号
